КОНСПЕКТ ЛЕКЦИЙ НАДЕЖНОСТЬ Б. Любые технические устройства всегда изготавливались в расчете на некоторый достаточный для практических целей период экономически эффективного использования
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
10. Методы повышения и обеспечения надежности Меры по обеспечению требуемой надежности принимаются на всех стадиях жизненного цикла объекта при его разработке, изготовлении, эксплуатации и утилизации. На стадии разработки применяют так называемые конструктивные методы: резервирование, стандартизация и унификация, комплектность ЗИП, оптимизация номенклатуры нормируемых показателей надёжности, выбор материалов, оптимизация конструкции, прогноз надёжности на основе анализа имеющегося опыта. На стадии изготовления применяют так называемые технологические методы (производственные): обеспечение оптимальности и стабильности технологических процессов, контроль качества материалов и изделий, применение технологических приёмов повышения надёжности, обкатка, контрольные испытания и др. На стадии эксплуатации применяют так называемые эксплуатационные методы: снижение нагрузок, защита от вредных воздействий, оперативная диагностика и контроль состояния, качественное техническое обслуживание (профилактика, планово-предупредительные ремонты, восстановление, квалификация персонала и т.д.), регистрация информации о надежности и др. Варианты применения методов повышения надежности так же многообразны, как и многообразны технические объекты. Тем не менее, можно выделить несколько основных групп этих методов: Разработка или выбор узлов и деталей высокой надежности. Подбор материалов и разработка методов и технологий их упрочнения. Стандартизация и унификация. Оптимизация режимов работы (нагрузок) основных элементов. Защита от перегрузок. Защита от внешних воздействий. Автоматизированное управление процессами и контроль. Оптимизация системы технического обслуживания и ремонта. Автоматизация и роботизация производства. Контроль качества на производстве. Контроль качества обслуживания при эксплуатации. Организационные мероприятия (обучение персонала, рабочие инструкции и т.д.). 10.1. Методы повышения структурной надежности Применение любых методов повышения надежности элементов не приведет к значительному эффекту при неудачной структурной схеме технической системы. Таким образом, важно обеспечить требуемую надежность самой структурной схемы объекта. Наиболее распространенными методами повышения надежности технических систем являются методы резервирования. Резервирование – применение дополнительных средств и/или возможностей с целью сохранения работоспособного состояния объекта при отказе одного или нескольких его элементов. Дополнительные возможности и средства обеспечиваются наличием различного рода резервов: алгоритмических; функциональных; программных; информационных; нагрузочных; временных; структурных и др. В соответствии с этим различают несколько видов резервирования: Временнóе резервирование применяется для создания запаса по времени и заключается в применении таких приемов, как завышение расчетного времени функционирования или расчетной производительности, применение накопителей, обеспечение требуемой функциональной инерционности элементов. Резервы времени расходуются на восстановление или замену отказавших элементов. Информационное резервирование применяется для компенсации искажения или потери передаваемой информации и заключается в повторении сообщений, передаваемых по одному каналу, параллельной передаче сообщения по нескольким каналам, кодировании информации. Функциональное резервирование заключается в придании элементу или объекту способности выполнять дополнительные, избыточные функции и достигается его функциональной универсализацией. Нагрузочное резервирование обеспечивается созданием запаса по нагрузке или введением защитных или разгружающих элементов, например, предохранительных устройств. Структурное резервирование осуществляется путем введения дополнительных элементов, функционально дублирующих основные элементы в случае их отказа. Существует несколько способов структурного резервирования. Классификация их по различным признакам приведена в табл. 6. Таблица 6 Классификация способов резервирования элементов систем
Структурное резервирование характеризуется кратностью – отношением числа резервных элементов к числу основных элементов. Резервирование с кратностью 1:1 называется дублированием. При любом способе структурного резервирования последовательные схемы соединений элементов надежности заменяются параллельными. Усилия по повышению надёжности оценивают коэффициентом выигрыша надёжности, равным отношению значений показателя надёжности до и после принятых мер: Gp=P1/P. ПРИМЕР 15 Найти коэффициент выигрыша надежности системы из n=3 последовательных равнонадежных элементов при резервировании одного из них, если вероятность безотказной работы этого элемента равна 0,8 и 0,9. Если в системе из n последовательных элементов продублировать (резервировать) один k–ый, то коэффициент выигрыша надежности будет равен: 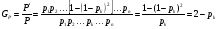 = 2-0,8 = 1,2 и 2-0,9 = 1,1. = 2-0,8 = 1,2 и 2-0,9 = 1,1.Эффект от резервирования любого элемента системы можно предсказать по значению производной по этому элементу вероятности безотказной работы. Рассмотрим это на примере простой системы (рис. 19). ПРИМЕР 16 2 3 1 Рис.19. Пример системы для резервирования Функция работоспособности системы имеет вид: А=а1а3+а2а3=А1+А2. По теореме умножения вероятностей Р(А1)=Р(а1а3)=р1р3, Р(А2)=Р(а2а3)=р2р3. По теореме сложения вероятностей Р(А)=Р(А1+А2)=1-(1-р1р3)(1-р2р3)=р1р3+р2р3-р1р2р3 (с учетом того, что одно и то же событие не может произойти одновременно дважды, т.е. сомножитель р32 не имеет смысла). Производные вероятности безотказной работы системы по элементам равны: Р1(р1)=р3-р2р3=(при р1=р2=р3)=р-р2. Р1(р2)=р3-р1р3=(при р1=р2=р3)=р-р2. Р1(р1)= Р1(р2). Р1(р3)=р1+р2-р1р2=(при р1=р2=р3)=2р-р2. Тогда разница Р1(р3) - Р1(р1)=р всегда больше нуля. Таким образом, выгоднее всего резервировать элемент под номером 3. В заключение следует отметить, что в рассматриваемых здесь и далее примерах резервирования не учитывается надежность переключателей - элементов, обеспечивающих подключение резервных элементов при отказах основных элементов. Другими словами, предполагается, что переключатели абсолютно надежны. На практике надежность переключателей должна учитываться, но для получения основных зависимостей и качественных выводов это не так важно, тем более что включение в расчеты надежности переключателей существенно их усложняет. Применяются два метода резервирования последовательно соединенных элементов: общее и раздельное (рис. 20). 1 2 n 1 2 n 11 21 n1 11 21 n1 a) б) Рис. 20. Нагруженное резервирование: а) – общее, б) - раздельное Выигрыш в надежности по вероятности безотказной работы при общем резервировании равен: Gp=Pp/P=(при P=pn и Pp=1-(1- 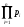 )2=р(2-р))=р(2-р)/р=2-р, )2=р(2-р))=р(2-р)/р=2-р,а при раздельном: Gp=Pp/P=(при P=pn и Pp= 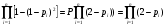 =(2-p)n. =(2-p)n.Раздельное резервирование эффективнее! ПРИМЕР 17 Определить эффективность резервирования элемента №3 на схеме по рис. 19 при равнонадежных элементах и вероятности их безотказной работы р=0,8. При равнонадежных элементах, вероятность безотказной работы основной системы равна: Р(А)=р2(2-р). При резервировании элемента №3 элементом №4 схема преобразуется в следующий вид: Система после резервирования 2 3 1 4 Функция работоспособности преобразованной системы имеет вид: А=а2а3+а2а4+а1а3+а1а4. Вероятности безотказной работы при событиях А1...А4: Р(А1)=Р(а2а3)=р2р3. Р(А2)=Р(а2а4)=р2р4. Р(А3)=Р(а1а3)=р1р3. Р(А4)=Р(а1а4)=р1р4. Тогда по теореме сложения вероятностей вероятность безотказной работы системы с резервированием: Рр(А)=Р(А1+А2+А3+А4)=1-(1-р2р3)(1-р2р4)(1-р1р3)(1-р1р4). Если мы произведем перемножения с учетом невозможности одновременной реализации одного и того же события, то при равнонадежных элементах получим: Рр(А)=4р2-4р3+р4=р2(2-р)2. Найдем Рр(А) иным способом. Система состоит из двух последовательных элементов, образуемых параллельным включением элементов 1-2 и 3-4. Тогда q12=q1q2, q34=q3q4 и P12=1-q1q2=1-(1-p1)(1-p2)= (при равнонадежных элементах)=1-(1-p)2=p(2-p); P34=1-(1-p3)(1-p4)=1-(1-p)2=p(2-p). Тогда Р(А)=Р(А1)Р(А2)=р2(2-р)2. Получен тот же результат! Коэффициент выигрыша надежности при резервировании элемента №3 равен: Gp=Pp/P=2-p=(p=0,8)=1,2. 10.2. Надежность систем при разных способах структурного резервирования Принципы расчета надежности систем с резервированием не отличаются от тех, что нами уже рассмотрены. Однако существуют некоторые специфические правила расчетов надежности систем с различными способами резервирования. Расчеты систем с нагруженным резервированием без восстановления проводятся как для параллельных и последовательных соединений. При этом считается, что отказ резервной группы (основной + резервный элементы) имеет место только после отказа последнего элемента. Надежность резервных элементов до и после отказа основного элемента не меняется, так как не меняется режим их работы. Для случая равнонадежных одного основного и n -1 резервных элементов вероятность отказа, вероятность безотказной работы и средняя наработка на отказ рассчитываются по схеме параллельного соединения и при экспоненциальном законе равны: 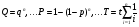 . .При ненагруженном резервировании методом замещения отказ системы произойдет тогда, когда откажет последний элемент. Надежность резервного элемента меняется, как только он включается в работу взамен отказавшего основного или предыдущего резервного (при многократном резервировании) элементов. При включении по методу замещения в схему резервной группы, состоящей из одного основного и n -1 резервных элементов, вероятность отказа уменьшается примерно в n! раз (при q < 0,1), значительно возрастают вероятность безотказной работы и средняя наработка на отказ (экспоненциальный закон распределения): 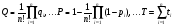 . .Ненагруженное резервирование дает больший выигрыш в надежности, чем нагруженное. О повышении надежности при резервировании см. также ЛР 6. Облегченное резервирование применяется в системах с большой инерционностью переходных процессов в случаях, когда горячее резервирование не обеспечивает требуемой надежности. Отказ резервной группы (основной + резервный элементы) произойдет лишь при отказе последнего элемента. Надежность резервного элемента различна в резервном и рабочем режимах. Точные формулы надежности системы с облегченным резервированием громоздки. При экспоненциальном законе распределения вероятность безотказной работы системы из равнонадежных элементов приблизительно равна: 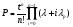 . .Здесь λр – интенсивность отказов при работе элемента в резервном режиме. ПРИМЕР 18 Показать, что ненагруженное резервирование дает больший выигрыш в увеличении средней наработки на отказ по сравнению с нагруженным резервированием (закон распределения экспоненциальный, элементы равнонадежны, резервная группа состоит из n элементов, один из них основной, остальные – резервные). При экспоненциальном законе распределения средняя наработка на отказ системы с n -кратно резервированным элементом при горячем резервировании равна: 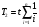 . .То же при ненагруженном резервировании: 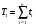 Выигрыш от ненагруженного резервирования в сравнении с нагруженным равен: 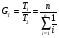 . Для n = 2 GT = 2/1,5 = 1,33, а для n = 10 GT = 10/2,93 = 3,41. . Для n = 2 GT = 2/1,5 = 1,33, а для n = 10 GT = 10/2,93 = 3,41.Структурное резервирование позволяет повысить надежность систем практически до любого уровня. Однако это сопряжено со значительными затратами, существенным увеличением числа элементов и серьёзным усложнением системы. В связи с этим существует проблема оптимального уровня надежности. Различают два основных типа задач оптимизации:
Под ресурсами подразумеваются все их виды: стоимость, вес, габариты, число элементов и др. В простейших случаях задача оптимального структурного резервирования сводится к определению элемента или элементов, резервирование которых дает наибольший эффект (наибольший коэффициент выигрыша). Наличие ограничений существенно усложняет задачу оптимизации. Без привлечения сложного математического аппарата уже не обойтись. Рассмотрение математических методов оптимизации выходит за рамки нашего курса. Особо следует рассмотреть системы с восстановлением элементов. Восстановление в системах без резервирования не изменяет вероятности безотказной работы, но повышает комплексные показатели надежности, например, коэффициент готовности. Иная ситуация в системах с резервированием. При резервировании восстановление является одним из методов повышения надежности в целом, в том числе и вероятности безотказной работы. Особенности расчета надежности резервированных систем с восстановлением обусловлены тем, что рассмотренные выше методы в данном случае практически неприменимы. Для систем с восстановлением наиболее часто применяют метод топологии и теории графов. Анализ надежности таких систем начинается с построения графа состояний и событий (переходов) системы. В заключение следует отметить, что структурное резервирование не является абсолютным методом повышения надежности любой системы. В системах с большими значениями наработки возможны ситуации (при больших значениях наработки), в которых резервированная система имеет меньшую вероятность безотказной работы, чем нерезервированная, т.е. оказывается менее надежной. |
