КОНСПЕКТ ЛЕКЦИЙ НАДЕЖНОСТЬ Б. Любые технические устройства всегда изготавливались в расчете на некоторый достаточный для практических целей период экономически эффективного использования

• Название: Любые технические устройства всегда изготавливались в расчете на некоторый достаточный для практических целей период экономически эффективного использования
• Анкор: КОНСПЕКТ ЛЕКЦИЙ НАДЕЖНОСТЬ Б.docx
• Дата: 16.12.2017
• Размер: 0.82 Mb.
• Имя файла: КОНСПЕКТ ЛЕКЦИЙ НАДЕЖНОСТЬ Б.docx
• Тип: Документы; #11661
• страница: 11 из 22

9.2. Методы анализа структурной надежности сложных технических систем (см. также ПЗ 2)
Целью расчетов надежности является оптимизация конструкции, выходных параметров, режимов эксплуатации, технического обслуживания и ремонта объекта с точки зрения обеспечения требуемой надежности. Достигнуть указанной цели можно лишь на основании анализа надежности.

Системный анализ надежности – анализ сложных технических систем в условиях взаимодействия и взаимного влияния составляющих систему элементов. Алгоритм системного анализа заключается в последовательности действий:

анализ объекта как сложной системы;

разработка математической модели надежности объекта;

расчет показателей надежности, характеризующих систему;

разработка технических и организационных мер обеспечения и повышения надежности системы и эффективности ее функционирования.

Анализ системы заключается в:

декомпозиции системы на подсистемы и элементы;

выборе критериев эффективного функционирования элементов, подсистем и системы в целом;

расчете и оптимизации параметров функционирования элементов, подсистем и системы в целом;

анализе отказов и причин их возникновения, а также влияния отказов элементов и подсистем на работоспособность системы в целом;

расчете показателей надежности элементов и подсистем.

Математическое моделирование надежности системы заключается в формальном описании системы в символьном (математические выражения) или топологическом (схемы и графы) виде.

При расчете надежности систем по условию безотказности обычно предполагают, что каждый элемент и вся система в целом могут находиться в одном из двух состояний: работоспособном или неработоспособном, а отказы элементов независимы друг от друга. В этом случае состояние системы определяется сочетанием состояний элементов. Поэтому расчет надежности системы может быть сведен к перебору комбинаций состояний элементов. Отношение суммы комбинаций работоспособных состояний к общему числу комбинаций состояний характеризует вероятность безотказной работы системы. Этот метод определения безотказности системы называется методом прямого перебора. Он применяется наряду с методами статистического моделирования, структурно-логического анализа и топологическими методами. Применение того или иного метода зависит, прежде всего, от структуры технической системы.

Функциональная структура любой технической системы отражает взаимодействие ее элементов. Структурная схема надежности системы зависит от цели ее функционирования.

Рассмотрим это на простых примерах (рис.9 - 11):
Схемы конструктивного соединения двух резистивных элементов

Структурные схемы элементов надежности при обрыве

Структурные схемы элементов надежности при замыкании

Рис. 9. Конструктивные и структурные схемы соединения элементов надежности при различных видах отказов резистивных элементов. Цель функционирования - наличие цепи и отсутствие КЗ

Схемы конструктивного соединения двух конденсаторов

Структурные схемы элементов надежности при обрыве

Структурные схемы элементов надежности при пробое

Рис. 10. Конструктивные и структурные схемы соединения элементов надежности при различных видах отказов конденсаторов. Цель функционирования – наличие цепи и отсутствие КЗ


Схемы конструктивного соединения двух фильтров для воды

Структурные схемы элементов надежности при засорении

Структурные схемы элементов надежности при разрыве

Рис. 11. Конструктивные и структурные схемы соединения элементов надежности

при различных видах отказов фильтров

9.2.1. Основные типы структурных схем надежности
Системы с последовательным соединением элементов

В последовательной структурной схеме соединения элементов надежности отказ любого из элементов влечет за собой отказ всей системы. Другими словами, система работоспособна, когда все ее элементы работоспособны.

Системы с такой структурной схемой соединения элементов встречаются в технике чаще других, поэтому последовательное соединение называют основным соединением. В таких системах применима теорема умножения вероятностей: вероятность одновременного появления независимых событий равна произведению вероятностей этих событий.

Другими словами, вероятность безотказной работы в течение некоторой наработки t системы из n независимых друг от друга элементов P(t) равна произведению вероятностей безотказной работы элементов p(t):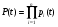

, (44)

При значениях безотказной работы элементов, близких к единице, вероятность безотказной работы системы может быть оценена приближённо как: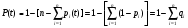

(45)

ПРИМЕР 9

Система состоит из n элементов высокой надежности. Вероятности безотказной работы элементов p близки к единице и практически одинаковы. Найти выражение для вероятности безотказной работы системы P и определить ее значение при n =2 и p =0,90; n =4 и p =0,99.

Для системы равнонадежных элементов справедливо равенство:

P=pⁿТогда Р=0.9²=0.81 и Р=0.99⁴=0.96.

ПРИМЕР 10

Доказать, что надежность системы со схемой последовательного соединения независимых элементов всегда ниже надежности самого ненадежного элемента системы.

Очевидно, что вероятность безотказной работы подобных систем всегда ниже вероятности безотказной работы самого ненадежного элемента. Если выделить самый ненадежный элемент k, то можно записать: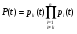

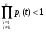. Поскольку p_i(t)<1, то и . Следовательно, P(t)<p_k(t).

Из этого следует, что в случае неизбежного применения ненадежных элементов недопустимо составлять структурную схему с их последовательным соединением.

Для указанных условий справедливо(44).

ПРИМЕР 11

Доказать, что интенсивность отказов системы из последовательно соединенных элементов надежности в случае экспоненциального закона распределения вероятности безотказной работы каждого из этих элементов при постоянной интенсивности отказов элементов также постоянна и равна их сумме.

Для экспоненциального закона распределения вероятности безотказной работы каждого элемента системы и при постоянной интенсивности отказов справедливо равенство: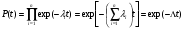

, (46)

где 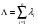- интенсивность отказов системы в целом.

Таким образом, в рассмотренных условиях интенсивность отказов системы равна сумме интенсивностей отказов составляющих её элементов.

Средняя наработка системы до отказа будет при этом равна Т=1/Λ.

В системе с элементами равной надежности Λ=nλ, а Т=t/n. Т.е. средняя наработка системы в n раз меньше средней наработки каждого элемента. Из (46) следует: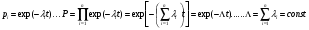



Системы с параллельным соединением элементов

В параллельной структурной схеме соединения элементов надежности отказ всей системы произойдет лишь при отказе всех ее элементов. Т.е. система откажет тогда, когда откажут все ее элементы. Параллельное соединение элементов характерно для технических систем с дублированием или резервированием, т.е. для систем, в которых приняты меры по повышению надежности. Хотя нередки случаи, когда параллельное соединение (конструктивное и структурное) является естественным элементом конструкции. Например, сдвоенные колеса на полуоси заднего моста грузовика, двух и четырехмоторные самолеты и т.д.

Вероятность отказа системы с параллельным соединением элементов надежности равна произведению вероятностей отказов всех ее элементов: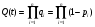

. (47)

Следовательно: 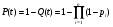. (48)

Чем больше параллельных элементов, тем выше вероятность безотказной работы системы.

Если выделить самый надежный элемент системы k, то: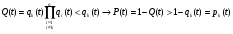

. (49)

Другими словами, вероятность безотказной работы системы из параллельных элементов надежности всегда выше вероятности безотказной работы самого надежного элемента. Значит, теоретически, из множества ненадежных элементов можно создать надежную систему при их параллельном соединении.

ПРИМЕР 12

Система состоит из равнонадежных параллельно соединенных элементов. Во сколько раз среднее время наработки до отказа такой системы больше среднего времени наработки до отказа элемента? Вычислить это увеличение для системы из двух элементов.

При экспоненциальном законе распределения вероятности безотказной работы системы из равнонадежных элементов можно записать: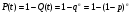

, откуда среднее время безотказной работы системы равно: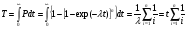

. (50)

Т.е. среднее время наработки до отказа такой системы больше среднего времени наработки до отказа элемента в 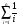раз.

При двух элементах этот коэффициент равен 1,5, при трех – 1,83.
Мажоритарная система представляет собой вариант системы с параллельным соединением элементов, в которой отказ происходит при потере работоспособности не всех ее элементов, а какой-то их части. Методы расчета надежности мажоритарных систем приведены в ПЗ 2.
9.2.2. Структурно-логический метод анализа системы
Структурно-логический анализ позволяет оценить основные показатели надежности объекта исходя из его конструктивных особенностей и взаимодействий составных частей, условий функционирования.

С точки зрения влияния на надежность системы в целом ее элементы подразделяют на четыре группы:

1. Элементы, отказ которых практически не влияет на работоспособность системы. Отказы этих элементов рассматриваются отдельно.

2. Элементы, работоспособность которых в течение рассматриваемой наработки практически не меняется, а вероятность их безотказной работы велика (близка к единице).

3. Элементы, ремонт или регулирование которых возможны в процессе работы или во время плановых остановок.

4. Элементы, отказ которых сам по себе или в сочетании с отказами других элементов приводит к отказу системы.

При анализе надежности системы в целом рационально рассматривать лишь элементы последней группы.

Большинство технических систем может быть представлено в виде совокупности элементов, соединенных последовательно или параллельно. Следует отметить, что параллельное или последовательное конструктивное исполнение элементов не всегда эквивалентно последовательному или параллельному соединению в схеме надежности.

В процессе структурно-логического анализа после проведения всех действий по выявлению возможных отказов, их причин и последствий, разделения системы на элементы с известными показателями надёжности, классификации этих элементов с точки зрения влияния на надёжность системы в целом, разрабатывается графическая модель безотказной работы, т.е. ее структурная схема надежности, по которой составляются расчетные зависимости для определения показателей надежности.
Методы минимального пути и минимального сечения
Минимальный путь (работоспособного состояния) – кратчайший путь функционирования; последовательный набор элементов в структурной схеме надежности, при котором система работоспособна, а отказ любого из этих элементов приводит к отказу системы.

Минимальное сечение (отказа) – минимальное аварийное сочетание; последовательный набор элементов в структурной схеме надежности, при котором система неработоспособна, а восстановление любого из этих элементов приводит систему в работоспособное состояние.

Эти методы эффективны при анализе мостиковых структурных схем надежности.

В мостиковых системах параллельные ветви элементов соединены между собой другими элементами. В простых случаях расчет надежности мостиковой системы может быть проведен методом прямого перебора, но с учетом положения элементов в схеме. Однако, в сложных системах формула работоспособного состояния (ФРС) сильно усложняется.

Если схема системы не сводится к одному из простых видов соединений, прибегают к логико-вероятностному методу ее анализа.

Рассмотрим пример простой мостиковой системы (рис. 12) и проанализируем ее надежность применяя логико-структурный метод.

ПРИМЕР № 14

4

2

1

3

5

Рис. 12. Мостиковая система
Техническим аналогом мостиковой системы может, например, являться система с двумя параллельно включаемыми насосами (элементы 1 и 2), двумя регулирующими вентилями (элементы 4 и 5) и перепускным клапаном (элемент 3). Цель функционирования - бесперебойная подача топлива.

Логические формулы, отображающие работоспособное и неработоспособное состояния системы, имеют вид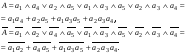



Логические формулы позволяют рассчитать показатели надежности системы, применяя теоремы сложения и умножения вероятностей.

С учетом сказанного, для системы по рис. 12 вероятность ее безотказной работы может быть вычислена по формуле

P=p₁p₄+p₂p₅+p₁p₃p₅+p₂p₃p₄–p₁p₂p₃p₄–p₁p₂p₃p₅–p₁p₂p₄p₅–p₁p₃p₄p₅–

–p₂p₃p₄p₅+2p₁p₂p₃p₄p₅.

Если все элементы системы равнонадежны, то P=2p²+2p³–5p⁴+2p⁵.

Логико-вероятностный метод довольно универсален, но в сложных случаях не всегда можно составить адекватную системе логическую функцию работоспособности. В теории надежности систем существуют методы рационализации логико-структурного метода. Мы их рассматривать не будем, поскольку это выходит за рамки нашего курса.
9.3. Вероятностные методы анализа надежности
9.3.1. Вероятностная модель внезапного отказа
Внезапные отказы по большей части происходят вследствие достижения предельного состояния материала, например, по критериям прочности (превышение запаса прочности), под воздействием внешних нагрузок. Внешние нагрузки определяются условиями работы объекта, внутренние – ошибками при разработке, производстве или эксплуатации. И нагрузка, и характеристика прочности носят вероятностный характер и имеют некие плотности распределения. От соотношения этих плотностей зависит вероятность наступления внезапного отказа (рис. 13).

Рис.13. Плотность распределения прочности (R) и нагрузки (S)

f

f(S)

f(R)

S,R

Вероятность отказа

M(S)

M(R)
Характеристики распределений прочности и нагрузки могут быть получены аналитически или путем обработки экспериментальных данных статистическими методами. На практике, при оценке надежности систем часто ограничиваются определением коэффициента запаса прочности, который определяется как отношение математического ожидания прочности к математическому ожиданию нагрузки. Однако, как это видно из рис. 13, даже при большом значении коэффициента запаса прочности существует вероятность отказа. Чем больше разброс значений прочности и нагрузки, тем эта вероятность выше. Вероятность безотказной работы объекта может быть определена аналитически по величине коэффициента запаса прочности с учетом законов распределений нагрузки и прочности. Это довольно трудоемкая задача, поэтому обычно ее стремятся упростить, определив критические, с точки зрения надежности, элементы с небольшим коэффициентом запаса прочности. Прибегают также к упрощенным выражениям. Например, считается, что запас прочности достаточен (P>0,999), если разница средних значений прочности и нагрузки больше или равна утроенной сумме среднеквадратических отклонений их математических ожиданий.

Таким образом, вероятностное моделирование внезапных отказов заключается в определении коэффициента запаса прочности и оценке его достаточности для обеспечения требуемой надежности.
9.3.2. Вероятностная модель постепенного отказа
Модели постепенных отказов рассматривают ситуации, когда параметры, характеризующие работу объекта, или его свойства, или внешние воздействия, меняются со временем, приближаясь и в конечном итоге достигая предельное значение. Область изменения параметра, в пределах которой сохраняется работоспособное состояние элемента или объекта, называется рабочей областью или полем допуска.
Изменение во времени параметра Х (со своим полем допуска) до достижения им предельного значения Х_пр

Плотность распределения средней наработки до отказа

t

Рис. 14. Схема постепенного (параметрического) отказа

Изменение интенсивности отказов

Вероятность безотказной работы

Параметрические отказы характерны для заключительной стадии работы объекта – стадии износа или старения.

На рис. 14 показана общая схема возникновения параметрического отказа в процессе постепенного изменения определяющего параметра в результате действия внутренних и внешних причин. С течением времени расширяется область возможных значений определяющего параметра и по мере развития процессов старения он достигает некоторого предельного значения. Наработка, при которой параметр достигнет предельного значения, величина случайная, а его среднее значение равно математическому ожиданию наработки до достижения параметром предельного значения для данного вида распределения случайной наработки. Поскольку с практической точки зрения доведение объекта до стадии ускоренного износа нежелательно, то в моделировании постепенных отказов обычно принимается постоянная для периода нормальной эксплуатации скорость изменения определяющего параметра. Соответственно и его предельное значение должно быть уменьшено, иначе расчётное значение наработки до отказа будет завышено.

Закон распределения вероятности безотказной работы будет зависеть от законов распределения определяющего параметра и наработки до достижения им предельного значения.

Таким образом, вероятностное моделирование параметрических отказов заключается в определении вероятности безотказной работы с учетом неопределенности значений определяющего параметра, скорости его изменения и времени достижения предельного значения.

Следует подчеркнуть, что кроме неопределенностей, упоминавшихся в двух предыдущих разделах, имеется, и может оказаться существенной, неопределенность внешних воздействий. Все это требует четкого описания, и даже установления определенных условий испытаний объектов на надежность. Только в этом случае допустимо и корректно сравнение их по показателям надежности. В противном случае необходимо знать и учитывать чувствительность данного показателя надежности к воздействиям.

Например, для наработки на отказ Т можно, пользуясь разложением в ряд Тейлора, записать ее зависимость от случайной нагрузки S в виде: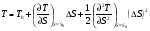

.

Здесь индекс «0» обозначает стандартные условия, а производные берутся в окрестностях точки S0 и характеризуют чувствительность показателя к изменениям нагрузки.

Если для данного объекта определён показатель для стандартных условий (обычно для номинальной нагрузки) и известны коэффициенты чувствительности к нагрузке, то его надежность может быть приблизительно охарактеризована, как это показано в выше приведенном выражении. Найти значения перечисленных коэффициентов можно по нескольким экспериментам, проведенным в разных условиях, решив соответствующую систему алгебраических уравнений.

Вероятность безотказной работы объекта по причинам внезапных и постепенных отказов равна произведению вероятностей безотказной работы для этих видов отказов.