Маг. 2012 Магистр. Научно-исследоват. практика. Магистерская и кандидатская диссертации по экономике методы и организация исследований, оформление и защита
 Скачать 1.7 Mb. Скачать 1.7 Mb.
|
|
Отступление 1.18. Об одном опыте проведения экспертного опроса // Инвестиции в России, 2001. №5. При решении задачи по количественному измерению составляющих К использовалась индивидуальная форма получения экспертных оценок в письменном виде на основе непосредственного контакта организаторов с экспертами. Именно такая форма позволяет получать более продуманные по времени и полные по содержанию ответы при максимальном использовании квалификации экспертов. С этой целью разрабатывалась специальная опросная анкета, состоящая из следующих частей: вводной, в которой раскрывается сущность задачи и порядок использования данных для получения окончательных суждений экспертов; инструктивной, содержащей подробные указания о порядке заполнения анкет; основной, которая содержит перечень частных критериев с градациями для оценки состояния; справочный, в которой каждый эксперт заносит о себе необходимые сведения (стаж работы в анализируемой области исследования, стаж работы в занимаемой должности, образование и т.д.), необходимые для расчетов коэффициентов Кn и Ки. Эксперты определяли значимость градации частных критериев и численное значение весов mi балльными оценками от 0 до 10. Например, начальник отдела объединения выступает в качестве эксперта и имеет следующие характеристики.
Поправочный коэффициент, характеризующий уровень квалификации и деловые качества начальника отдела объединения будет равен Кn = 0,1 (5,77 + 4,29 + 8,32 + 5,47 + 8,52)/5 = 0,647. Кn = 0,1 (5,77 + 4,29 + 8,32 + 5,47 + 8,52)/5 = 0,647. Для этого, в частности, может служить показатель средней компетентности (dj), исчисленный по формуле средней арифметической, взвешенной с учетом значимости каждого способа. 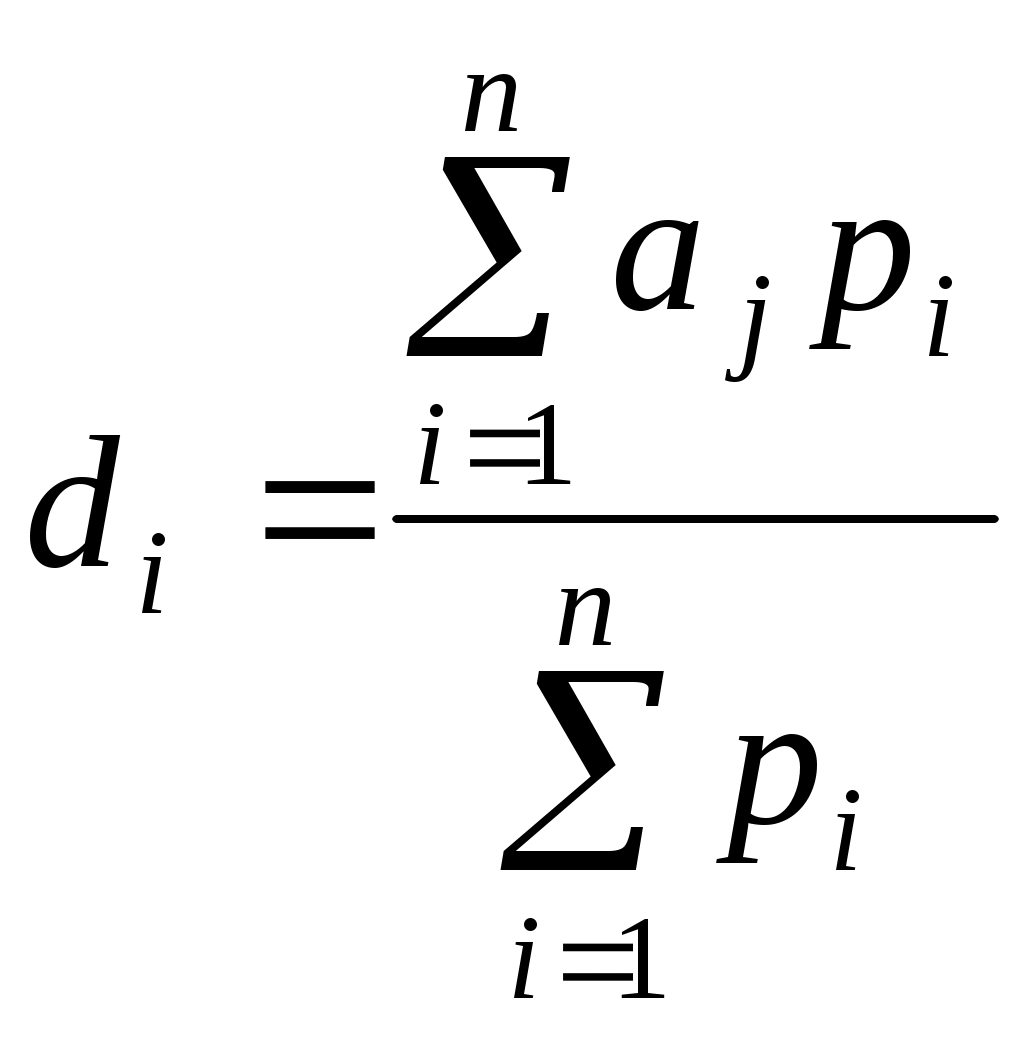 , , где Так как оценки экспертов представляют собой случайные величины, то необходимо количественно измерять согласованность их мнений. Для оценки совпадений мнений экспертов можно рекомендовать использование коэффициента конкордации (согласованности) – W. где S – сумма квадратов отклонений сумм рангов (ответов, данных всеми экспертами на каждый вопрос) от среднего значения суммы рангов по данному предмету (объекту) исследования ( Тогда где Ri – ранги, присвоенные каждому вопросу i-ым экспертом; m – число экспертов; n – число вопросов. Пример применения методики расчета коэффициента конкордации, которая может быть использована при подборе группы экспертов, приведен ниже. Пусть имеется десять вопросов, характеризующих компетентность каждого эксперта в области знания рисков хозяйственной деятельности предприятия. В экспертную группу предполагается включить пять специалистов, которые являются экспертами в этой сфере знаний. Данные и расчеты по ним представлены в таблицах 1.2 и 1.3. Таблица 1.2 Ранги ответов, данных экспертами, на вопросы
Таблица 1.3 Название
По данным таблицы 1.3 исчисляется коэффициент согласованности рангов: Так как коэффициент конкордации служит мерой общности суждений экспертов, очевидно, что при совпадении мнений экспертов, его величина равна 1. Если различия во мнениях очень велики, коэффициент конкордации приближается к 0. В данном примере он приближен к 1. Другими важными задачами, решаемыми в рамках метода экспертных оценок, являются построение шкал, ранжирование, парное и последовательное сравнения и другие процедуры экспертных измерений. Но поскольку наиболее важной задачей в применении этого метода, как уже отмечалось, является подбор экспертов, ей и уделено особое внимание. Другие же процедуры Вы можете изучить по специальной литературе. Математическое моделирование и модели в экономических исследованиях: обзор необозримого Новые знания в научных исследованиях можно получать и в процессе экспериментов. В естественных и технических науках эксперимент иногда является основным средством производства новых знаний. В экономических же проведение эксперимента не всегда возможно и оправдано, поскольку может оказаться очень дорогим. Для решения этих задач в экономических исследованиях лучше применять математическое (и не только математическое) моделирование. В общем и целом, под моделью принято понимать упрощение некоей реальной целостности (объекта, системы, процесса, идеи) путем представления ее в другой, более удобной для восприятия, анализа и экспериментов (исследований) форме. Так, в частности, схема организационной структуры предприятия представляет его модель, на которой, проектируя, например, более эффективную систему управления, можно изображать новые подразделения, прослеживать направления материальных и информационных связей между ними и т.п. Согласитесь, уважаемый читатель, что на модельной схеме производить подобные эксперименты гораздо проще и нагляднее, чем на реальном объекте (т.е. прямо на самом предприятии). Возможность проведения экспериментов на моделях (по-другому, модельных исследований) и составляет их основное достоинство. В исследовании экономических систем, при получении новых знаний о них, всегда возможны ошибки. И очевидно, что лучше совершать эти ошибки, экспериментируя на моделях, чем на реальных объектах. Так будет намного дешевле. В теории и практике моделирования выделяют несколько классов моделей: физические, аналоговые, математические и имитационные. В литературе можно встретить и другие классификации. Они отличаются от выше приведенной либо названиями классов, либо более подробным подразделением на них, либо тем и другим вместе. Физическая модель представляет собой выполненный в масштабе материальный объект моделируемой целостности. Это может быть, к примеру, уменьшенная модель самолета, предназначенная для изучения его аэродинамических свойств. Так называемых фотомоделей, очевидно, тоже можно (как это ни странно звучит) отнести к данному классу, поскольку они представляют собой физическое воплощение общепринятых, или разделяемых группой экспертов, представлений об одежде, красоте, манерах и т.п. Физические модели являются точными копиями моделируемых объектов и ведут себя похожим образом. Но поскольку они меньше и проще самих объектов, то эксперименты по установлению их свойств обходятся намного дешевле. Так, например, очевидно, что установление пределов аэродинамического давления путем регулируемого изменения нагрузки на модель самолета до ее разрушения будет неизмеримо меньше, чем проведение таких испытаний на готовом самолете. Равно как и апробация новых образцов одежды на фотомоделях также будет дешевле (хотя само по себе это мероприятие вряд ли можно назвать дешевым), чем запуск этих образцов в производство с надеждой, что они будут пользоваться спросом на рынке. Аналоговая модель представляет реальный объект не точной его копией, как это имеет место при физическом моделировании, а совершенно другим объектом, который выглядит по-иному, но вместе с тем ведет себя так или очень похоже, как моделируемая целостность. Если физические модели в управлении предприятиями используют не очень часто, то аналоговые в этой сфере человеческой деятельности находят довольно широкое применение. К их числу относится любой график производственно-хозяйственной деятельности. Так, в частности, график безубыточности показывает, при каком объеме производства того или иного продукта предприятие преодолеет барьер превышения издержек над выручкой. Схема организационной структуры также представляет собой аналог системы управления на предприятии. Известный венгерский экономист Янош Корнаи в книге «Дефицит» уподобил национальную экономику сообщающимся сосудам, в которых переливающаяся жидкость служит аналогом переливания капиталов из отрасли в отрасль. Можно привести и массу других примеров применения аналоговых моделей в управлении. Математические модели представляют собой чрезвычайно большой и структурно разветвленный класс моделей. При этом диапазон структурной разветвленности очень широк. Неполный перечень видов и разновидностей экономико-математических моделей, характеризующий этот диапазон, представлен на страницах данной книги. Кроме того, математические модели отличаются друг от друга и своей сложностью. И здесь диапазон различий также является очень широким. Так, в частности, математическая модель может быть представлена в виде одной формулы. Например, формула расчета точки безубыточности является математической моделью, в то время как график безубыточности, о котором говорилось чуть выше, аналоговой моделью того же самого состояния предприятия, оцениваемого по параметрам издержек и выручки. В этом случае график как модель визуально показывает зоны убыточности и прибыльности, определяемые объемами производства. Формула же как модель позволяет при заданных величинах постоянных затрат, а также переменных, приходящихся на единицу продукции, и цены вычислять тот объем производства, при котором выручка сравнивается с издержками. Другими словами, у каждой модели свои преимущества. Математическая модель – другая крайность – может быть представлена и в форме взаимосвязанных уравнений, неравенств, выраженных в математической форме условий, с огромным числом переменных. Наиболее простыми из них являются модели линейного программирования, в которых уравнение представляет собой целевую функцию, выражающую, например, максимизацию прибыли, а неравенства – ограничения на имеющиеся ресурсы. Аналогичную форму и структуру имеют родственные линейному программированию модели дискретной оптимизации, нелинейного программирования и др. Иногда математические модели могут включать в себя элементы аналоговых моделей. К их числу, например, можно отнести модели сетевого планирования, в которых математические зависимости дополняются сетевыми графиками. В отечественной высшей школе применение математических моделей подробно изучается в курсах экономико-математического моделирования, по которым издано большое число учебной литературы (см., например, [11, 16, 21]). Несмотря на то, что класс математических моделей, которые используются в экономических исследованиях, чрезвычайно широк и невозможно в одном пособии сделать полный обзор всему многообразию их видов и разновидностей (можно сказать, классов экономико-математических моделей), тем не менее, есть смысл коротко остановиться на наиболее известных из них, хорошо проявивших себя в организации эффективных экономических исследований. Соискатель, производящий научный поиск, хотя бы в общих чертах должен знать о них, с тем, чтобы, обратившись к специальной литературе и изучив ее досконально, мог применить те или иные методы математического моделирования в своих прикладных исследованиях. Обзор действительно будет очень кратким, без формул, уравнений, неравенств и т.п. Однако для предварительного знакомства с этим классом методов научного поиска его будет более чем достаточно. Подробное же изучение каждого класса математических моделей следует изучать по специальной литературе. Очень широкое (возможно, самое широкое) распространение в экономических исследований получили модели линейного программирования. Они применяются для определения оптимального способа распределения ограниченных ресурсов при наличии альтернативных направлений их использования. Ясно, что различные наборы ресурсов (сырья, материалов, труда, рабочего времени работников и т.п.) можно использовать для производства различных продуктов. Расчеты на моделях линейного программирования показывают, в каких объемах должно осуществляться производство каждого из этих продуктов, чтобы расход имеющихся ресурсов был экономичным и эффективным, а результат - оптимальным. При этом линейная модель производит и весьма специфическую информацию, называемую двойственными оценками, которые показывают, на сколько может измениться общий результат деятельности (критерий оптимальности) при увеличении или уменьшении расхода того или иного ресурса на единицу. Таким образом, двойственные оценки, по сути, количественно показывают степень дефицитности имеющихся ресурсов, что при корректном использовании модели может стать точным инструментом балансирования на предприятии затрат и результатов. Есть множество вариаций постановки задач линейного программирования: с ориентацией на максимизацию прибыли, минимизацию расходов, составление оптимальных смесей (задача о диете), минимизацию расходов по доставке грузов (транспортная задача) и др. Для задач, в которых используется дискретная информация, разработаны модели целочисленного программирования, для задач, в которых важной составляющей является время – модели динамического программирования и др. Расчеты на моделях линейного программирования носят итерационный (пошаговый) характер, поэтому «вручную» они возможны только на задачах небольшой размерности. Но и при этом они настолько трудоемки и утомительны, что в «ручной» практике почти не применяются. Но поскольку в настоящее время есть компьютерные программы, реализующие расчеты на моделях линейного программирования, то и необходимости в расчетах на бумаге нет никакой. Наряду с моделями линейного программирования в практике управления весьма широко применяются и модели управления запасами. Само название этого класса моделей говорит об их назначении. Очевидно, что любая организация должна поддерживать соответствующий ее производственным потребностям уровень запасов. Для производственной фирмы требуются определенные поставки сырья, материалов, полуфабрикатов, а также определенный задел незавершенного производства и запас готовой продукции, для предприятий общественного питания – продуктов и напитков в ассортименте, для больниц – лекарств и т.п. Очевидно также и то, что поддержание запасов на необходимом уровне требует определенных затрат, которые подразделяются на три вида: на размещение заказов и доставку; на хранение; на потери, обусловленные несоответствующим (большим или малым) уровнем запасов. Модели управления запасами позволяют так согласовать эти и другие переменные, что затраты на поддержание необходимых запасов будут сведены к минимуму. Предприятиям, предлагающим населению различного рода услуги, хорошо могут помочь модели теории очередей. Суть этого класса моделей сводится к уравновешению расходов на содержание фирмой дополнительных каналов обслуживания и потерь от обслуживания меньшего числа каналов. Под каналом обслуживания в разных фирмах могут пониматься совершенно разные объекты. Так, в частности, в парикмахерской это кресла (и, естественно, парикмахеры), в банке – кассиры, в ремонтной мастерской – рабочие места мастеров и т.п. Определение оптимального числа каналов обслуживания для фирм, продающих услуги, является чрезвычайно важной задачей. Увеличение, например, числа кассиров в банке (ввод дополнительных каналов обслуживания) сверх оптимального, приведет к повышению затрат, обусловленных их содержанием. Сокращение кассиров (экономия на их заработной плате и содержании рабочих мест) может привести к увеличению очередей и потере клиентов, которые предпочтут покупать услуги в другом банке, где очередей нет. Где находится та «золотая середина», уравновешивающая эти две противоположности, и показывают модели теории очередей. В условиях рынка не последним фактором внешней среды является конкуренция. Обеспечение конкурентоспособности продукции практически всегда приводит фирму к успеху, поэтому к ее повышению стремятся все организации. При осуществлении мер повышения конкурентоспособности прогноз возможных действий конкурентов, в ответ на свои действия, всегда оборачивается для фирмы большим преимуществом. Оценку воздействия того или иного решения на конкурентов позволяют получить модели теории игр. Этот класс моделей может предсказать возможную реакцию конкурентов на изменение цен, новую маркетинговую стратегию, если ее можно выразить количественно и т.п. Модели теории игр применяются в экономических исследованиях значительно реже описанных выше. Причина, очевидно, кроется в том, что их «предсказания» сбываются не так часто и они менее точны, чем «предсказания» других моделей, ибо в них, в отличие, например, от моделей управления запасами, в неизмеримо большей степени задействован человеческий фактор. А он, как известно, всегда вносит некую (иногда и весьма существенную) «сумятицу» в строгую логику математических зависимостей. Но все-таки, уважаемый читатель, согласитесь, что очень хочется иногда предугадать (вычислить, а почему бы и нет?) возможные действия конкурентов в ответ на те или иные собственные шаги. Поэтому для настоящих исследователей модели теории игр никогда не утратят своей привлекательности. Не все параметры исследуемых экономических систем могут быть уложены в строгие математические зависимости, что, безусловно, усложняет процесс математического моделирования. Кроме того, иногда большое число переменных создает непреодолимые трудности для математического анализа зависимостей между ними. Высокий уровень неопределенности внешней среды также отнюдь не способствует получению высокоточной информации в процессах модельных исследований. Да и человеческий фактор, о котором уже неоднократно упоминалось выше и который неизбежно присутствует в деятельности любой организации, существенно затрудняет реализацию математических моделей в управлении предприятиями. Для преодоления всех этих трудностей и применяются так называемые имитационные модели. В общем и целом, имитационное моделирование представляет собой дополнение тех или иных математических моделей, в традиционном их понимании, различными алгоритмами и компьютерными программами, имитирующими реальные процессы. В качестве таких дополнений иногда выступают и люди, являющиеся экспертами в области моделируемых процессов. Они анализируют полученную в результате модельных исследований информацию, обсуждают результаты индивидуального анализа каждого из экспертов и выносят общее заключение, которое учитывается на следующем шаге (итерации) эксперимента. Такие имитационные модели (с включением экспертов) довольно часто называют деловыми играми. Иногда совокупность математических моделей и тех или иных имитационных блоков, действующих совместно, называют имитационными системами. Если основную часть такой системы составляет программное обеспечение, ее называют модельным компьютерным стендом (или просто модельным стендом). Работа таких стендов происходит в режиме «если, то», т.е. в модель вводятся заранее определенные данные, производятся расчеты, а затем анализируются полученные результаты. На основе последних делаются корректировки вводимых данных, после чего приступают к следующему шагу (итерации) модельных исследований. И так до тех пор, пока результаты не будут удовлетворять исследователей. Такие имитационные системы позволяют определять приемлемые структуру и величины входов с тем, чтобы результаты выходов (продуктов и т.п.) реальных процессов отвечали требованиям проводимого исследования (целям, стратегиям, установкам). Поскольку в имитационных моделях (системах) описываются процессы, все они являются динамическими. На создание такой системы на исследуемом предприятии может уйти много времени и средств. Но зато она может работать в течение длительного времени, ее можно изменять, приспосабливать к меняющимся условиям внешней среды. Другими словами, имитационные модели (системы) являются адаптивными, а следовательно, они (при условии определенной корректировки) могут применяться в течение длительного времени и первоначальные затраты, понесенные на их создание, будут оправданы. Большой класс представляют модели статистической теории решений. Это, в свою очередь, тоже труднообозримая сфера применения математических методов в экономических исследованиях. Одной из наиболее простых и наглядных моделей этого класса является так называемая платежная матрица, помогающая менеджеру при принятии решения осуществить выбор приемлемой альтернативы из нескольких имеющихся. Под платежом в данном случае понимается денежное вознаграждение или полезность, являющиеся следствием вполне конкретной стратеги поведения менеджера (или фирмы) в определенных условиях внешней среды, не зависящих от воли и сознания исследователя. Представленные в форме двумерной таблицы платежи по разным вариантам (наименования строк таблицы) и условиям осуществления (или неосуществления) этих вариантов (наименования колонок таблицы) образуют платежную матрицу, работа над которой и позволит исследователю выбрать приемлемый вариант решения. Как «нельзя объять необъятное», по крылатому выражению Козьмы Пруткова, так нельзя и обозреть необозримое. Поэтому в пособии представлены только основные классы математических моделей, которые неплохо зарекомендовали себя в экономических исследованиях. Теперь, если в сфере поисковой исследовательской деятельности читатели испытывают определенный недостаток в информации, есть возможность сориентироваться в ситуации, выбрать необходимый класс моделей по пособию, изучить его по специальной литературе с тем, чтобы, разработав и отладив необходимые модели, получить новые знания, являющиеся результатом исследований (экспериментов) на моделях. Исследователю-экономисту также весьма полезно знать о порядке и процедурах разработки математических моделей. Это тем более важно, что на начальных этапах разработки моделей он должен принимать непосредственное участие в формулировании их общей идеологии. В общем и целом, процесс разработки модели состоит из следующих пяти этапов: постановка задачи; построение модели; проверка модели на достоверность; применение модели; обновление модели. Постановка задачи является не только первым, но, пожалуй, и самым ответственным этапом в экономико-математическом моделировании. Точное и корректное использование математики и компьютерных технологий не принесет никакой пользы, если сама проблема не будет точно определена (сформулирована). При диагностике проблемы, с тем, чтобы отличить симптомы от причин, должен быть применен научный подход, состоящий в свою очередь из трех фаз: наблюдения, формирования гипотезы и верификации. Наблюдение в этом случае представляет собой сбор необходимой информации, которая и позволит «отделить зерна от плевел» (причины от симптомов). На основе собранной информации выявляются возможные альтернативы действий и последствия каждой из них для сложившейся ситуации. Сравнение последствий реализации альтернатив позволяет сделать выбор в пользу одной из них, что кладется в основу гипотезы в модельных экспериментах. На фазе верификации осуществляется проверка выдвинутой гипотезы, производятся первые предварительные оценки выбранной альтернативы. На этапе постановки задачи, по сути дела, надо сделать выбор класса модели (линейного программирования, имитационной модели и др.) и определить ее параметры. В решении проблем постановки задачи исследователь должен быть предельно внимательным и осторожным, ибо как будет поставлена задача, такими будут и результаты модельных исследований. Что толку в верной с точки зрения математики модели, если проблема исследования не была изначально точно диагностирована. И кому как не исследователю-экономисту решать, какой именно должна быть модель, чтобы она ему предоставляла не просто верную, но, самое главное, полезную информацию. О важности точного определения проблемы сказано уже очень много (см. отступление 1.19). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
