мат мет-лекции-ИНТЕРНЕТ. Математические методы в психологии

• Название: Математические методы в психологии
• Дата: 01.06.2022
• Размер: 2.19 Mb.
• Имя файла: мат мет-лекции-ИНТЕРНЕТ.doc
• Тип: Документы; #561290
• страница: 9 из 35

Тема 5 Исследование взаимосвязи признаков

Понятие корреляции

Корреляция – это согласованность изменения признаков. Если два явления изменяются синхронно и эти изменения можно выразить количественно, то между показателями этих явлений будет наблюдаться корреляция. Например, корреляция может наблюдаться между ростом и весом людей (большая вероятность, что чем выше человек– тем больше будет его вес). Или между уровнем интеллекта и показателями школьной успеваемости.

Нельзя говорить, что корреляция представляет собой выражение зависимости одного явления от другого, так как корреляция не всегда предполагает наличие причинно-следственной связи.

Корреляции бывают как линейные, так и нелинейные. Нелинейной может быть, например, связь между уровнем мотивации и эффективностью выполнения задачи (так называемая кривая мотивации Йеркса-Додсона). При повышении мотивации эффективность выполнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации, которому соответствует максимальная эффективность выполнения задачи; дальнейшему повышению мотивации сопутствует снижение эффективности (См. рис.).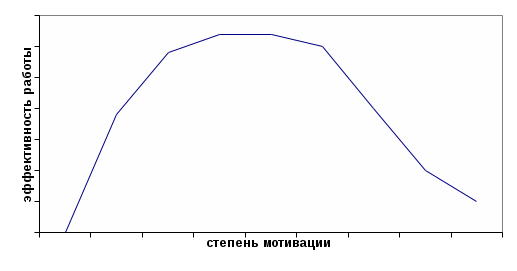



Линейную корреляцию можно количественно измерить. Степень связи между признаками выражается величиной, называющейся коэффициентом корреляции. Значения данного коэффициента (обозначается чаще всего буквой R или r) могут находиться в диапазоне от +1 до –1. В случае прямой пропорциональной зависимости одного признака от другого значение коэффициента приближается единице. Отрицательный коэффициент свидетельствует о разной направленности варьирования признаков: при изменении одного

в сторону увеличения – другой уменьшается. Например, показатели интеллектуальной ригидности отрицательно коррелируют с уровнем интеллекта, и положительно - с показателями интеллектуальной настойчивости. Величина близкая к нулю говорит об отсутствии взаимосвязи между признаками.

Данные, полученные при корреляционном исследовании, обычно изображают в виде диаграммы рассеивания, на которой каждая переменная откладывается на своей оси, а каждая точка отражает одиночное измерение. Выше изображен пример графического представления линейной корреляции между показателями роста в сантиметрах и веса в килограммах у представителей группы студентов СПбАА. Если бы коэффициент корреляции был равен +1, то точки на графике выстроились бы в ровную линию. В настоящем примере этот коэффициент составляет r = 0,76.

Какова прогностическая значимость вычисления корреляций? Оно помогает установить, можно ли предсказывать возможные значения одного показателя, зная величину другого.

К 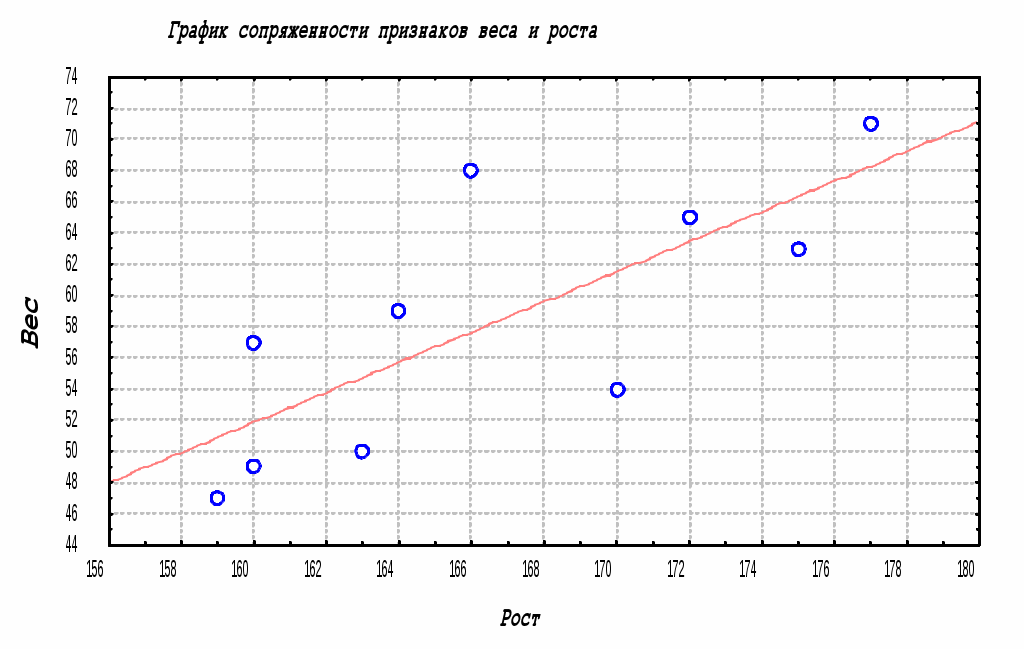оэффициент корреляции это безразмерная величина и не зависит от масштабов измерения. Например, сила связи между ростом и весом будет одной и той же независимо от того, проводились ли измерения в дюймах и футах или в сантиметрах и килограммах.

В зависимости от типа шкалы, в которой измерены переменные, используют различные виды корреляции. Таким образом, выделяют следующие виды корреляции: линейную (метрическую), ранговую и между номинативными переменными. Если данные измерены в интервальной или абсолютной шкале и укладываются в кривую нормального распределения, то применяется метод линейной корреляции. При этом используется вычисление коэффициента корреляции по Пирсону.

Если метрические данные не подчиняются закону нормального распределения, то рекомендуется преобразовать метрические данные в ранговые и применить метод ранговой корреляции. Этот же метод используется при работе с переменными, измеренными в порядковой шкале. В этом случае используют вычисление коэффициента ранговой корреляции по Спирмену или по Кендаллу.

Для анализа зависимостей номинативных переменных используют критерий С-Пирсона, хи-квадрат Пирсона, (не путать последние два с линейной корреляцией Пирсона!), точный критерий Фишера, статистику фи-квадрат.

Классификации коэффициентов корреляции

Коэффициенты корреляции характеризуются силой и значимостью.

Классификация коэффициентов корреляции по силе.

сильная	r > 0,70
средняя	0,50 < r < 0,69
умеренная	0,30 < r < 0,49
слабая	0,20 < r < 0,29
очень слабая	r < 0,19

Классификация коэффициентов корреляции по значимости.

Высокозначимая корреляция	r соответствует уровню статистической значимости p ≤ 0,01
Значимая корреляция	r соответствует уровню статистической значимости p ≤ 0,05
Незначимая корреляция	r не достигает уровня статистической значимости p>0,1

Не следует путать 2 этих классификации, так как они определяют разные характеристики. Сильная корреляция может оказаться случайной и, стало быть, недостоверной. Особенно часто это случается в выборке с малым объемом. А в большой выборке даже слабая корреляция может оказаться высокозначимой.