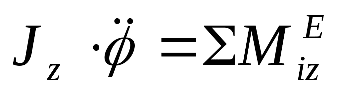Механическая система
1. Дайте определение механической системы.
Механическая система – совокупность взаимодействующих между собой материальных точек.
2. Какие классификации сил Вам известны.
Внутренние и внешние силы.
3. Дайте определение внутренним и внешним силам системы.
Внутренними называют силы взаимодействия между точками данной механической системы.
Внешними называют силы, с которыми на точки данной механической системы действуют окружающие тела, не входящие в систему.
4. Запишите дифференциальные уравнения движения механической системы.
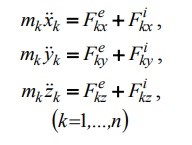
5. Дайте определение центра масс механической системы
Центр масс механической системы – геометрическая точка, для которой сумма произведений масс всех материальных точек, образующих механическую систему, на их радиус-векторы, проведенные из этой точки, равна нулю.
6. Сформулируйте теорему о движении центра масс.
Центр масс механической системы движется как материальная точка с массой, равной массе всей системы, к которой приложена сила, равная главному вектору внешних сил.
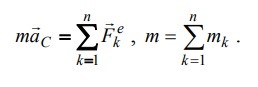
7. Сформулируйте следствия из теоремы о движении центра масс.
Следствия:
1. Если главный вектор внешних сил равен нулю, то центр масс движется равномерно и прямолинейно или находится в покое.
2. Если проекция главного вектора внешних сил на какую-либо из осей равна нулю, то по отношению к этой оси центр масс движется равномерно или соответствующая координата центра масс постоянна.
3. Внутренние силы не влияют на движение центра масс.
Моменты инерции
1. Дайте определение момента инерции системы точек относительно оси.
Момент инерции тела (системы) относительно оси называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси.
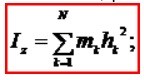
где mk - масса к-ой точки, hk - ee удаление от оси z.
2. Какие есть еще моменты инерции кроме момента инерции относительно оси?
- Центробежный момент инерции;
- Геометрические моменты инерции;
- Момент инерции относительно плоскости;
- Центральный момент инерции.
- Тензор инерции и эллипсоид инерции
3. Запишите моменты инерции некоторых сплошных тел, относительно оси, проходящей через центр масс.
Стержень:
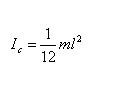
где m – масса стержня, l – длина стержня.
Диск:
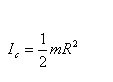
где m– масса диска; R – радиус диска.
Цилиндр:

Кольцо:

4. Запишите момент инерции стержня относительно оси проходящей через конец стержня.

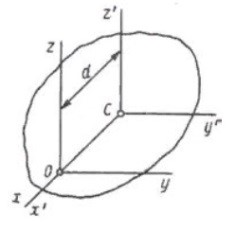
5. Сформулируйте теорему Гюйгенса.
Момент инерции механической системы относительно любой оси равен моменту инерции механической системы относительно центральной параллельной оси (оси проходящей через центр масс) увеличенному на произведение массы механической системы на квадрат расстояния между осями:
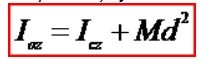 
Меры движения и меры действия сил.
1. Какие существуют меры движения?
К мерам движения относят следующие характеристики их инертности и движения: количество движения (импульс) точки и системы, кинетический момент (момент количества движения) точки и системы относительно точки и оси, кинетическую энергию точки и системы.
2. Чему равно количество движения точки и системы.
Количество движения материальной точки (импульс) – векторная мера ее движения, равная произведению массы точки на ее скорость.
Количество движения механической системы– векторная мера движения, равная сумме количеств движения точек системы.
Вектор количества движения механической системы равен произведению массы системы на скорость центра масс: 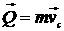 . .
3. Чему равен кинетический момент точки и системы.
Момент количества движения материальной точки (кинетический момент) относительно центра ? это вектор, определяемый равенством: 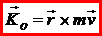 . .
Главный момент количеств движения (или кинетический момент) механической системы относительно центра О или оси Z равен соответственно геометрической или алгебраической сумме моментов количеств движения всех точек системы относительно того же центра или оси 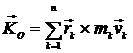 , , 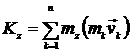 . .
4. Чему равна кинетическая энергия точки.
Кинетическая энергия материальной точки - скалярная мера ее движения, равная половине произведения массы точки на квадрат ее скорости.
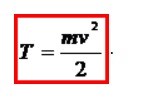
5. Чему равен кинетический момент вращающегося с угловой скоростью твердого тела относительно оси вращения.
Кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела.
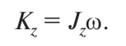
6. Запишите выражение для кинетической энергии тела при поступательном движении.
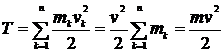
7. Запишите выражение для кинетической энергии тела при вращательном движении.
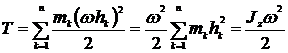
8. Запишите выражение для кинетической энергии тела при плоскопараллельном движении.
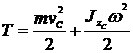
9. Какие меры действия сил Вы знаете?
- Элементарный импульс силы;
- Импульс силы за конечный промежуток времени;
- Элементарные работы силы;
- Работа силы на конечном перемещении.
10. Что такое элементарный импульс силы?
Элементарный импульс силы – векторная мера действия силы за элементарный промежуток времени dt:
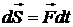 . .
11. Чему равна элементарная работа силы?
Элементарная работа силы – скалярная мера действия силы на элементарном перемещении dr точки ее приложения, определяемая скалярным произведением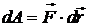
12. Напишите формулу для определения работы силы тяжести.
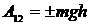
Знак «+», если точка приложения силы тяжести опускается.
13. Чему равна элементарная работа силы, приложенной к вращающемуся телу.

Элементарная работа силы, приложенной к вращающемуся телу, равна произведению момента силы относительно оси вращения на элементарный угол поворота тела.
14. Какую систему сил называют консервативной.
Силы, работа которых не зависит от пути, по которому двигалась частица, а зависит лишь от начального и конечного положений частицы, называются консервативными.
Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия
Моуль 1 1. Сформулируйте основные задачи статики.
Изучение методов преобразования одних систем сил в другие, эквивалентные данным.
2. Дайте определение силы.
Сила - мера механического воздействия одного тела на другое. Физическая природа сил в механике не рассматривается.
3. Чем характеризуется сила?
Сила задается модулем, направлением и точкой приложения
4. Как определяется модуль силы?
Модуль равнодействующих двух сил определяется по формулам: F=F1 + F2
5. Как задается направление силы в пространстве?
Аналитически силу можно задать ее проекциями на оси координат: , , , а направление в пространстве - направляющими косинусами: , , .
6. Что такое система сил?
Совокупность нескольких сил, действующих на твердое тело, называется системой сил.
7. Дайте определение равнодействующей.
Сила, эквивалентная данной системе сил, называется равнодействующей: .
8. Дайте определение уравновешенной произвольной системы сил.
Систему сил, приложенную к свободному твердому телу, находящемуся в равновесии, и не выводящую его из этого состояния, называют уравновешенной системой сил
0.
9. Дайте определение абсолютно твердого тела.
Абсолютно твердое тело - тело, у которого расстояние между любыми двумя очками остается неизменным.
10.Когда системы сил эквивалентны?
Две системы сил эквивалентны (
) между собой, если, не нарушая состояния тела, одну систему сил можно заменить другой.
11.Сформулируйте аксиому статики о равновесии твердого тела под действием двух сил.
Абсолютно твердое тело находится в равновесии под действием двух сил тогда и только тогда, когда эти силы равны по модулю, действуют по одной прямой и направлены в противоположные стороны.
12.Сформулируйте аксиому статики об уравновешенной системе сил.
Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать уравновешенную систему сил.
13.Можно ли переносить силу вдоль линии ее действия.
Точку приложения силы можно переносить вдоль линии действия силы.
14.Сформулируйте аксиому статики о равнодействующей двух сил.
Две силы, приложенные к телу в одной точке, имеют равнодействующую, проходящую через эту точку и равную их геометрической сумме.
15.Сформулируйте аксиому статики о силах взаимодействия двух тел.
Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.
16.Сформулируйте аксиому отвердевания.
Равновесие деформируемого тела не нарушится, если это тело отвердеет.
17.Дайте определение свободного тела.
Тело называется свободным, если его перемещение в пространстве ничем не ограничено.
18.Дайте определение несвободного тела.
Тело называется несвободным, если его перемещение в пространстве ограничено.
19.Какие тела называются связями?
Тела ограничивающие перемещения несвободного тела называются связями.
20.Что такое реакции связей?
Силы, с которыми связи действуют на несвободное тело, называются реакциями связей.
21.Какие силы называются активными?
Активными будем называть те силы, которые продолжают действовать на тело и после освобождения его от связей.
22.Дайте определение идеальной нити.
Идеальная нить (гибкая, невесомая, нерастяжимая): Примеры: моделирует трос, канат, цепь, ремень, Реакция идеальной нити направлена по нити к точке подвеса.
23.Дайте определение идеальному стержню.
Идеальный стержень (жесткий, невесомый стержень, на концах которого шарниры): Реакция связи направлена по стержню. Стержень может работать на сжатие.
24.Сформулируйте аксиому освобождаемости от связей.
Всякое несвободное тело можно считать свободным, если мысленно освободиться от связей, а их действие заменить соответствующими реакциями.
25.Какая система сил называется сходящейся?
Силы называются сходящимися, если линии их действия пересекаются в одной точке.
26.Сформулируйте теорему о сходящейся системе сил.
Система сходящихся сил имеет равнодействующую, которая равна геометрической сумме этих сил и проходит через точку пересечения их линий действия.
27.Как определить равнодействующую системы сходящихся сил геометрически?
Геометрически равнодействующая может быть найдена как замыкающая сторона силового многоугольника.
28.Как определить равнодействующую системы сходящихся сил аналитически?
Аналитически по проекциям на оси координат
29.Запишите и сформулируйте условия равновесия системы сходящихся сил в векторной форме.
Равенства выражают условия равновесия в аналитической форме: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.
30.Запишите и сформулируйте условия равновесия системы сходящихся сил в проекциях на оси декартовой системы координат.
Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекция всех сил на каждую из трёх выбранных любым образом координатных осей равнялись нулю.
31.Сформулируйте условия равновесия системы сходящихся сил в геометрической форме.
Геометрическое условие равновесия сходящихся сил формулируется так: для равновесия системы сходящихся сил необходимо, чтобы их геометрическая сумма равнялась нулю, т.е. чтобы силовой многоугольник, построенный на слагаемых силах, был замкнут.
32.Какие задачи называются статически определенными.
Задача статики о равновесии называется статически определимой, если количество неизвестных не превышает количества уравнений.
33.Всегда ли существует равнодействующая системы сходящихся сил?
Только если силовой многоугольник построенный на силах системы, будет замкнутым.
34.Сформулируйте теорему о трех силах.
Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
1. Сформулируйте теорему об изменении количеств движения системы.
Теорема: Производная по времени от количества движения механической системы равна сумме всех внешних сил, действующих на систему.
2. Сформулируйте закон сохранения количеств движения системы.
Если главный вектор внешних сил системы равен нулю, то количество движения системы не изменяется.
3. Могут ли внутренние силы изменить количество движения системы?
Внутренние силы, действующие между точками механической системы, не влияют на изменение количества движения системы.
4. Сформулируйте теорему об изменении кинетического момента механической системы относительно центра и оси.
Теорема: Производная по времени от кинетического момента механической системы относительно некоторого неподвижного центра равна геометрической сумме моментов всех внешних сил, действующих на систему, относительно того же центра.
Теорема: Производная по времени от кинетического момента механической системы относительно неподвижной оси равна сумме моментов всех внешних сил, действующих на систему, относительно этой оси
5. Сформулируйте законы сохранения кинетического момента относительно центра и оси.
Относительно центра:
1. Внутренние силы, действующие между точками механической системы, не влияют на изменение кинетического момента механической системы.
2. Если главный момент внешних сил системы относительно какого-либо центра равен нулю, то кинетический момент системы относительно этого центра не изменяется.
Относительно оси:
Если сумма моментов внешних сил относительно какой-либо оси равна нулю, то кинетический момент системы относительно этой оси постоянен.
6. Сформулируйте теорему об изменении кинетической энергии.
Теорема: Изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на систему, на том же перемещении.
7. Запишите дифференциальные уравнения поступательного движения тела.
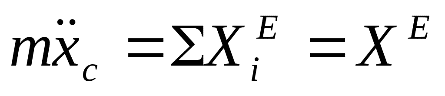
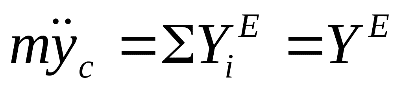
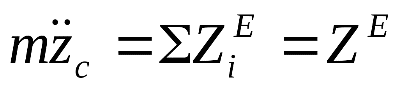
Здесь m – масса тела, xc, yc, zc - координаты центра масс тела;
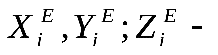 проекции внешней силы проекции внешней силы 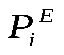 на оси координат, на оси координат,
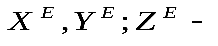 проекции главного вектора внешних сил проекции главного вектора внешних сил 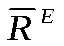 на эти оси. на эти оси.
8. Запишите дифференциальные уравнения вращательного движения тела.
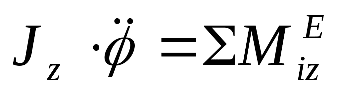
где Jz - момент инерции.
М - главный момент внешних сил относительно оси вращения.
? - угол поворота тела.
9. Запишите дифференциальные уравнения плоского движения тела.
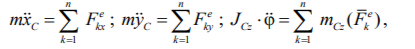
где xC, yC – координаты центра масс;
? - угол поворота тела;
J -момент инерции относительно оси, перпендикулярной плоскости движения и проходящей через центр масс; ,
F – проекции внешних сил на оси координат. |
 Скачать 114.16 Kb.
Скачать 114.16 Kb.
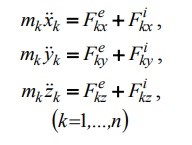
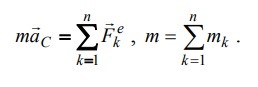
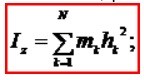
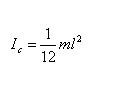
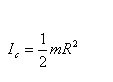



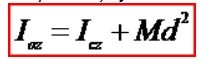

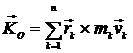 ,
, 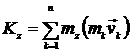 .
.
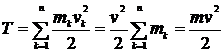
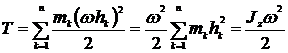
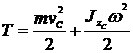
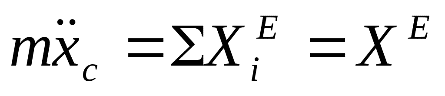
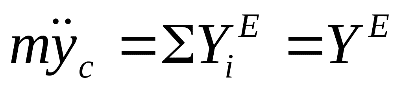
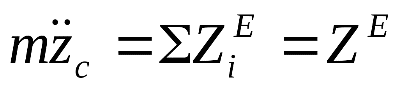
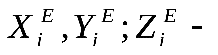 проекции внешней силы
проекции внешней силы 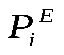 на оси координат,
на оси координат,