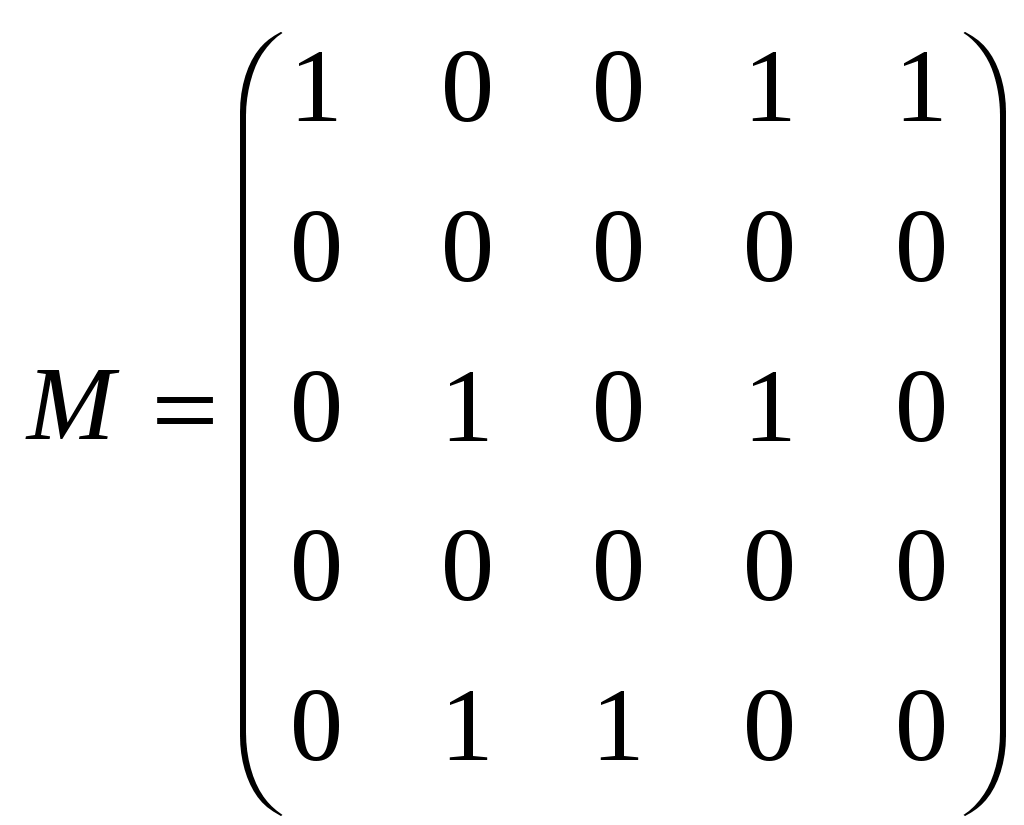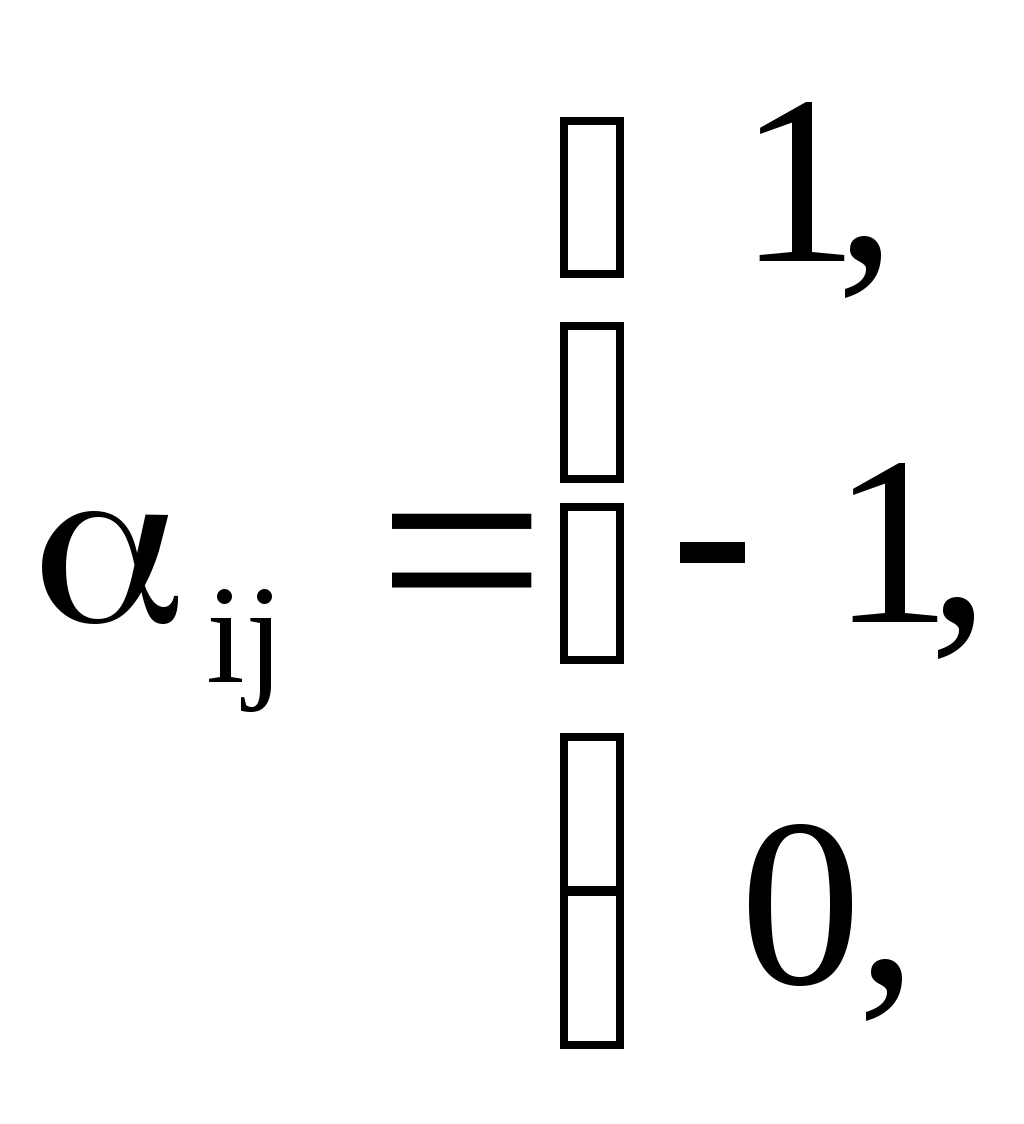УПП_Дискретная математика-1. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики

• Название: Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
• Дата: 09.02.2023
• Размер: 6.65 Mb.
• Имя файла: УПП_Дискретная математика-1.doc
• Тип: Учебно-практическое пособие; #929287
• страница: 10 из 19

Теория графов

3.1. Графы

Бинарное отношение на конечном множестве X есть ориентированный конечный граф (орграф) RX². Таким образом, всякий орграф определяется множествами:

X={x₁,x₂,…,x_n} – множеством вершин графа и множеством упорядоченных пар (кортежей);

R={i,x_j>|x_iRx_j} – множеством дуг графа.
Общепринято обозначать орграфы в виде

G(X,U),

где X – множество вершин орграфа;

U – множество дуг орграфа, или в виде

G(x, гx),

где ГX = {Гx₁,Гx₂,…,Гx_n} – множество образов элементов множества X, т.е. отображение X в X, понимая термин отображение как точечно-множественное отображение.

Наряду с орграфами в приложениях рассматриваются неориентированные графы. Неориентированный граф является частным случаем орграфа, в котором для каждой дуги i,x_j> существует ей параллельная и противоположно направленная дуга j,x_i>, т.е. бинарное отношение R обладает свойством симметрии. Если, кроме того, бинарное отношение R обладает свойством рефлексивности, то соответствующий ему ориентированный граф есть орграф-толерантность, содержащий дуги типа петля i,x_i> для всех вершин графа.

При геометрической реализации неориентированного графа вместо двух дуг i,x_j> и j,x_i>, соединяющих вершины x_i и x_j, употребляется одно ребро (x_i,x_j), не имеющее ориентации. На рис. 3.1.1 приведены геометрические реализации орграфов (слева) и их неориентированных аналогов – неориентированных графов (справа). G' (Х', U') есть подграф графа G(X, U), если X'X; U'U, т.е. подграф G' получим из графа G, если уберем какое-либо число вершин или ребер (дуг).

Две вершины графа называются смежными, если они соединены друг с другом.

Дуги называются смежными, если конец одной из них совпадает с началом другой.

Некоторая последовательности смежных дуг называется путем, а последовательность смежных ребер называется цепью.

Замкнутый путь называется контуром, а замкнутая цепь – циклом.

Сформулированные определения удобно представить в виде следующей таблицы:

Ориентированный граф	Неориентированный граф
Дуга	Ребро
Путь	Цепь
Контур	Цикл

Рассмотрим еще некоторые определения, которые нам понадобятся в дальнейшем. Путь (цепь) называется элементарным, если он проходит через вершины графа по одному разу.

Путь (цепь) называется простым, если он проходит через дуги графа по одному разу. В противном случае путь (цепь) называется составным. Аналогично определяются и простые контуры и циклы.

Цепь (цикл) называется гамильтоновой, если она проходит через все вершины графа по одному разу, т.е. элементарная цепь, проходящая через все вершины графа, есть гамильтонова цепь.

Цепь (цикл) называется эйлеровой, если она проходит через все ребра по одному разу, т.е. простая цепь (цикл), содержащая все ребра графа есть эйлерова цепь (цикл).

Аналогично определяются гамильтоновы и эйлеровы пути и контуры.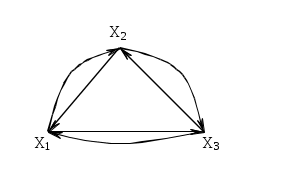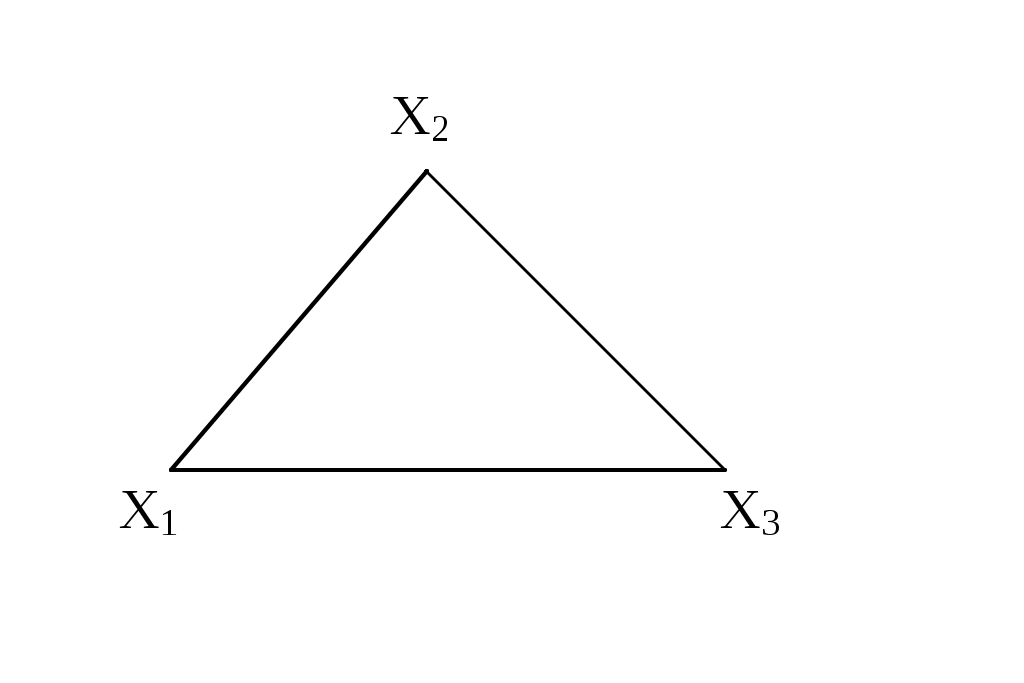



Симметричный граф Неориентированный граф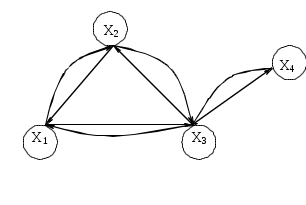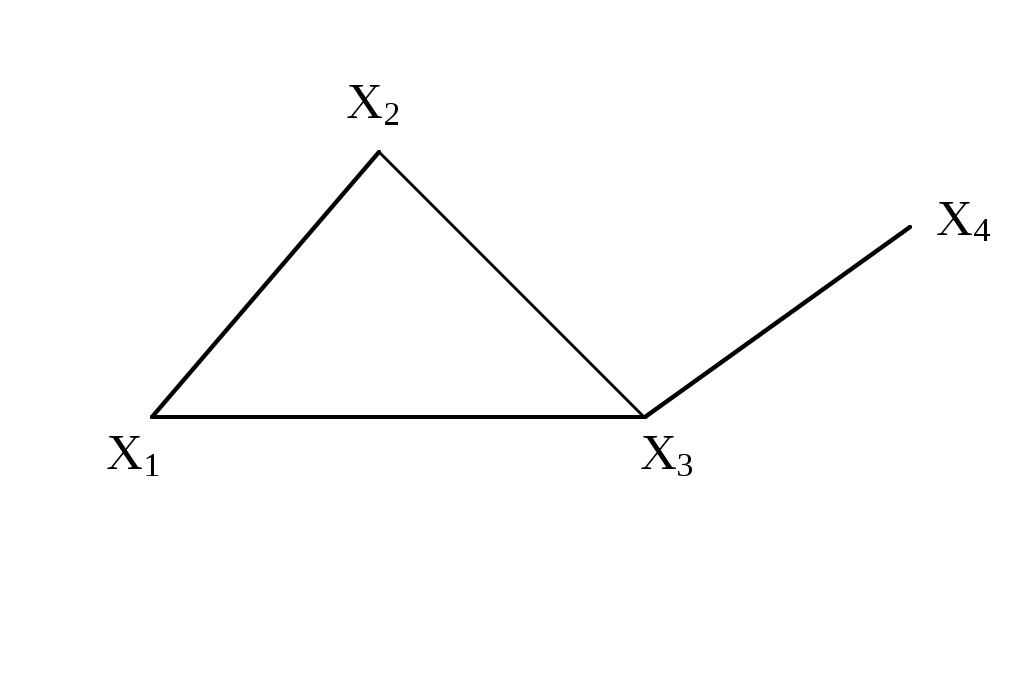


Граф-толерантность Неориентированный граф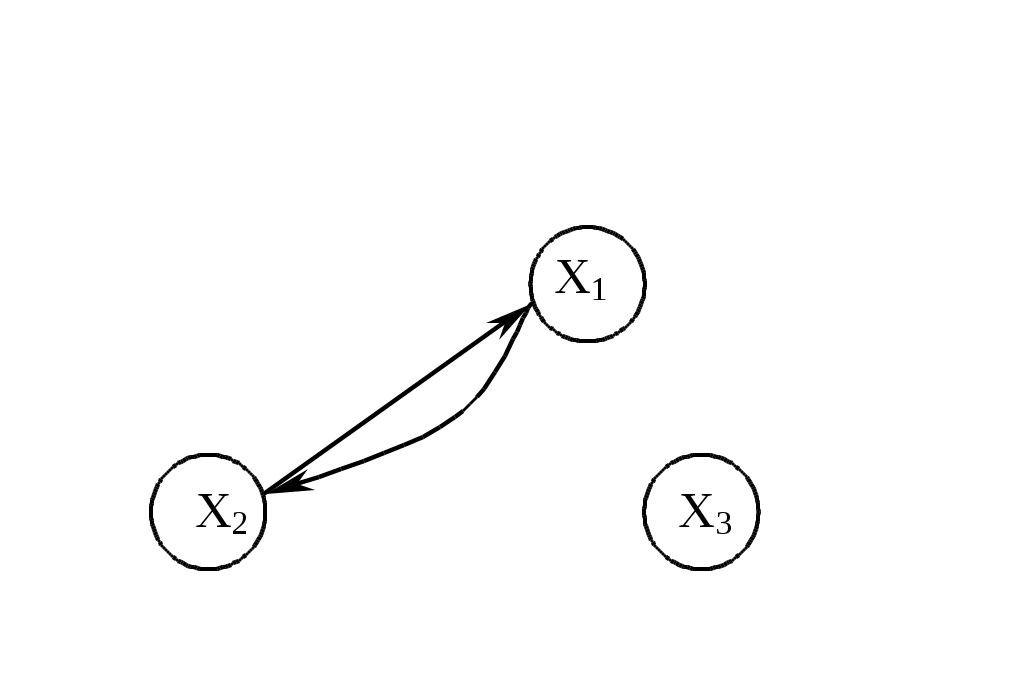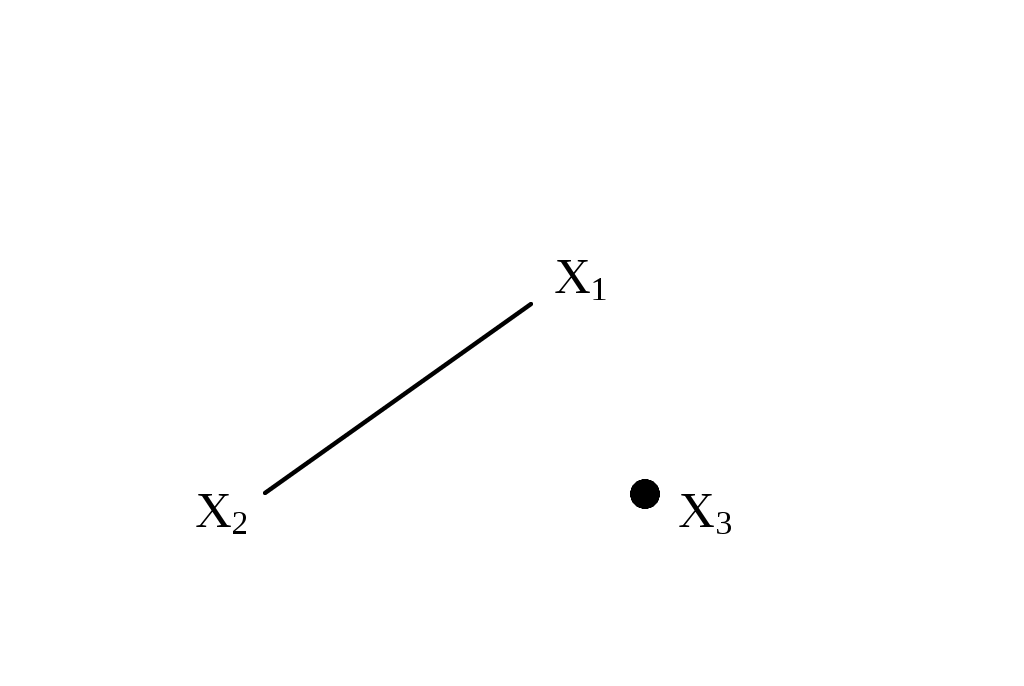


Граф-толерантность Неориентированный граф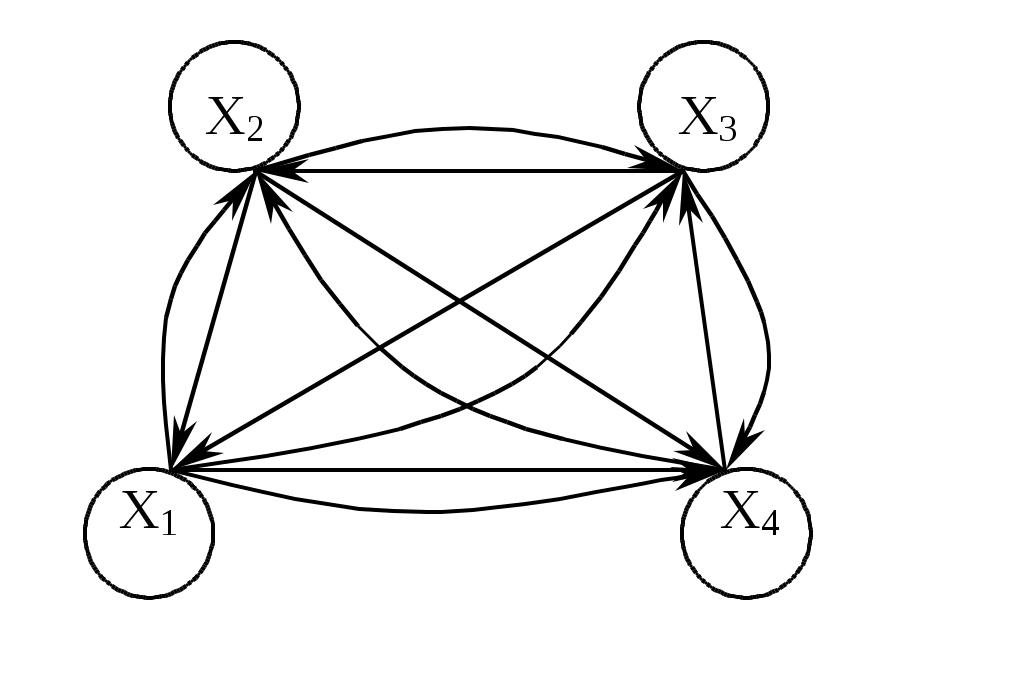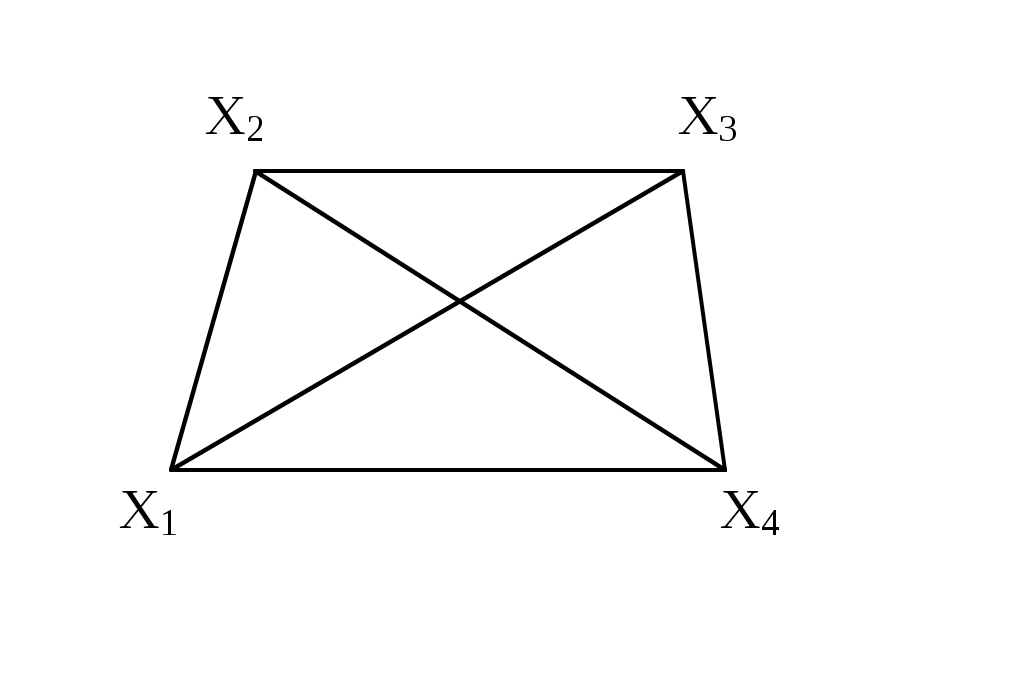


Граф-декартово произведение Неориентированный

(с полным насыщением) полный граф
Рис. 3.1.1

Степень вершины графа. Число ребер графа
Вершина X_i называется инцидентной дуге (ребру) графа, если она является началом или концом этой дуги (ребра).

Степенью вершины графа называют число дуг (ребер), инцидентных данной вершине. Степень обозначается P(X_i).

Для ориентированного графа различают полустепень захода P⁺ – число дуг, входящих в данную вершину, и полустепень исхода P^- – число дуг, выходящих из данной вершины. Степень вершины ориентированного графа составит сумма полустепеней исхода и захода.

P(X_i)= P⁺(X_i)+P^-(X_i).

Если для некоторой вершины ориентированного графа полустепень захода некоторой вершины P⁺=0 и при этом полустепень исхода P^-0, то вершина называется входом графа.

Если для некоторой вершины ориентированного графа P^-=0, а P⁺0, то вершина называется выходом графа.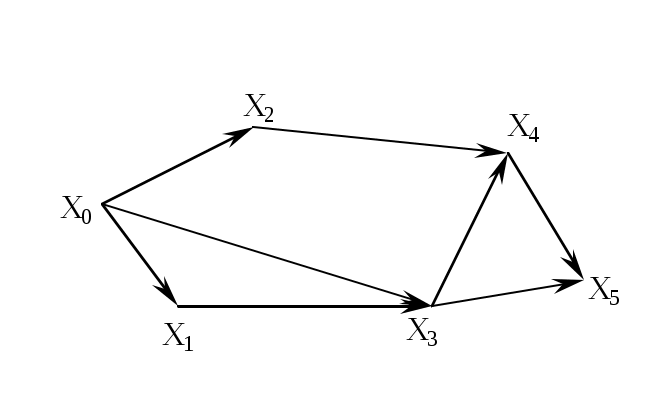



Рис. 3.1.2
Граф, изображенный на рис. 3.1.2, имеет один вход – вершину X₀

(P^-(X₀)=3) и один выход – вершину X₅ (P⁺(X₅)=2).

Число ребер графа N связано со степенями его вершин следующим соотношением:

N= ,

где n – число вершин графа. Отсюда следует справедливость следующих утверждений:

1. 
   Сумма степеней вершин любого графа четна;
   
2. 
   Для любого графа число вершин, имеющих нечетные степени, четно;
   
3. 
   Для однородного графа, т.е. графа, все степени вершин которого одинаковы и равны r, N= ;
   
4. 
   Для полного графа, т.е. графа, в котором каждая пара вершин соединена ребром или дугой, P(X_i)=n-1, а N= .
   

Некоторой противоположностью полному графу является нуль-граф, не имеющий ребер или дуг и состоящий из изолированных вершин. Очевидно, степени вершины нуль-графа равны 0.
Связность
Граф называется связным, если множество его вершин нельзя разбить на два или более подмножеств так, чтобы ни одна вершина одного подмножества не отображалась в вершину другого. В противном случае граф называется несвязным. Число подмножеств, не связанных отображениями, на которое разбивается множество всех вершин графа, называется числом компонент связности для несвязного графа.

Существует другое определение связности графа. Граф называется связным, если две любые его вершины можно соединить цепью. Граф (рис. 3.1.3) является несвязным с двумя компонентами связности.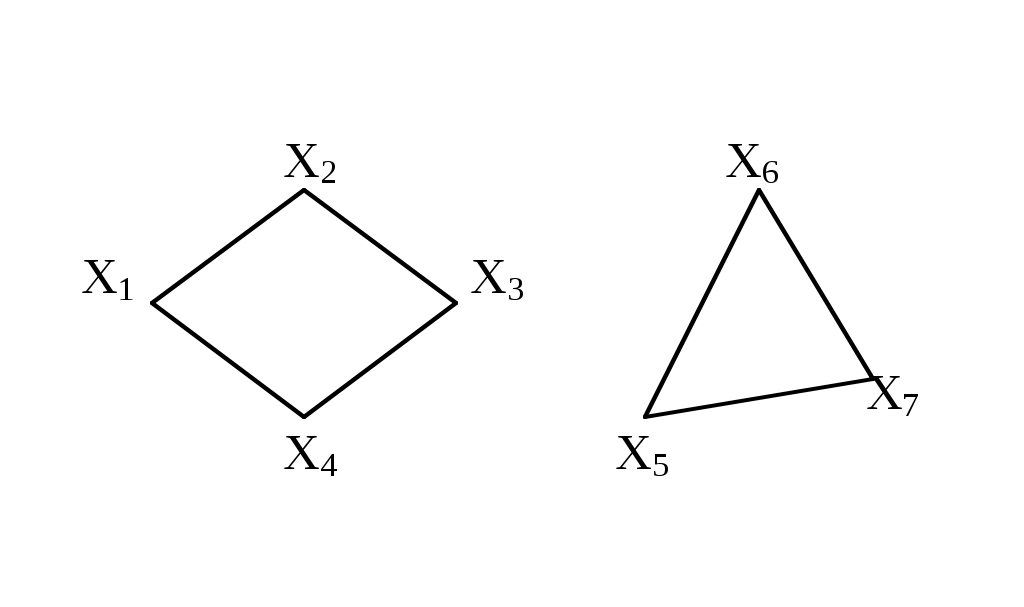



Рис. 3.1.3

Ребро графа называется перешейком, или связующей линией, если его удаление приводит к тому, что граф становится несвязным. На рис. 3.1.4 изображены три связных неориентированных графа, причем граф 1 не имеет ни одного перешейка, 2 содержит один перешеек (отмечен жирной линией), граф 3 целиком состоит из одних перешейков. Такой граф (3) называется деревом.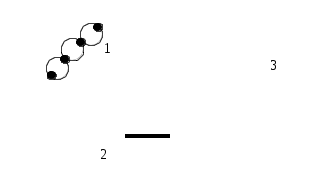


Рис. 3.1.4

Эйлеровы и гамильтоновы цепи и циклы.

Теоремы Эйлера
Рассмотрим задачу о кенигсбергских мостах, сформулированную Эйлером. Река Прегель делит г. Кенигсберг на четыре части: A, B, C, D, соединенные между собой семью мостами (рис. 3.1.5).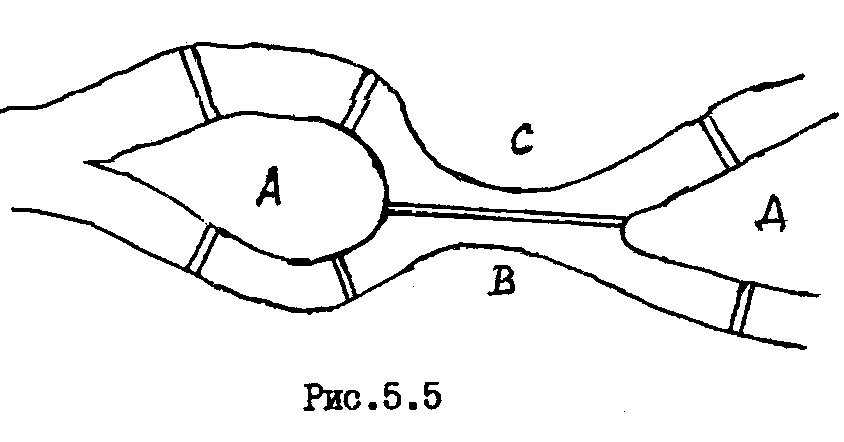



Рис. 3.1.5

Требуется определить, можно ли, выйдя из какой-либо части города, пройти по всем мостам по одному разу и вернуться в исходную часть города. Решая эту задачу, Эйлер доказал теоремы, позволяющие установить, для каких графов существуют эйлеровы циклы и цепи.
Теорема 1. Чтобы неориентированный граф обладал эйлеровым циклом, необходимо и достаточно, чтобы он был связен, и все вершины графа имели четные степени.

Для существования эйлерова контура на ориентированном графе необходимым и достаточным условием являются связность графа и равенство полустепеней захода и исхода в каждой вершине. Очевидно, что степени вершин графа четны.

Граф, соответствующий задаче Эйлера о кенигсбергских мостах, не удовлетворяет теореме 1. Он не содержит эйлерова цикла.
Теорема 2. Неориентированный граф содержит эйлерову цепь, соединяющую вершины А и В в том и только в том случае, если граф связен, и только эти вершины А и В являются вершинами с нечетными степенями, а степени всех остальных вершин четны.

Алгоритм построения эйлерова цикла состоит в следующем:

1. 
   Выходим из произвольной вершины X₀, каждое пройденное ребро зачерчиваем.
   
2. 
   Никогда не идем по такому ребру, которое в рассматриваемый момент является перешейком, а также не выбираем ребра, идущего в X₀, пока есть другие возможности.
   

Задача об определении гамильтоновых линий в общем виде не решена. Для каждого графа она решается отдельно. Получены некоторые необходимые, некоторые достаточные условия существования гамильтоновых графов, т.е. графов, содержащих гамильтонов цикл. К полученным результатам относится теорема Кенига: в полном графе (т.е. в графе, любая пара вершин которого соединена хотя бы в одном направлении) всегда существует гамильтонов путь.

К числу задач, требующих определения гамильтонова цикла, относится задача о коммивояжере. Бродячий торговец, предлагая товар, посещает ряд городов, причем каждый город он посещает единственный раз, после чего вновь возвращается в исходный пункт. Требуется определить кратчайший путь коммивояжера, если расстояния между городами заданы. Города можно представить как вершины связного неориентированного графа, в котором каждый паре вершин x_i, x_j приписывается расстояние l(x_i,x_j). Эта задача имеет ряд важных приложений в экономике, к ней, в частности, сводится задача о наиболее эффективном использовании подвижного состава оборудования. Решается задача методами динамического программирования.
Изоморфизм графов
Два графа называются изоморфными (от греч. «изос» – «равный» и «морфе» – «вид», «форма»), если между их вершинами можно установить взаимно однозначное соответствие, сохраняющее смежность, т.е. два графа G(x,u) и G'(x',u') изоморфны, если существует такое взаимно однозначное соответствие  , что если ,то ,где
.
Изоморфные графы несут одну и ту же информацию, поэтому они могут рассматриваться как один граф. Графы различаются с точностью до изоморфизма.
Планарность. Плоские графы
Говорят, что граф укладывается на поверхности S, если его можно нарисовать на S так, что никакие два его ребра не пересекаются в точках, не являющихся вершинами графа.

Граф называется планарным, если его можно уложить на плоскости. Плоский граф – граф, уложенный на плоскости.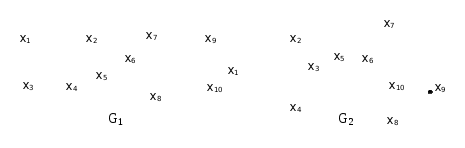



Рис. 3.1.6
Граф G1 (рис. 3.1.6) планарен, он изоморфен плоскому графу G2. Исследование планарности графов составляет одну из задач этой теории. Изучение планарных графов было начато Эйлером. Опираясь на результаты, полученные Эйлером, можно доказать, что графы K₁, K₂, K₃ (рис. 3.1.7) не являются планарными. Заметим, что графы K₁, K₃ изоморфны.


Рис. 3.1.7
Графы, изоморфные указанным графам, также не являются планарными.

Отыскание общего критерия планарности графов составляло одну из труднейших задач теории графов. Решение было найдено Понтрягиным и независимо от него Куратовским. Чтобы сформулировать эти результаты, необходимо познакомиться с определением гомеоморфизма. Но прежде сформулируем следующие определения.

Говорят, что граф G'(x',u') получен из графа G(x,u) операцией подразделения ребра (x_i,x_j)u, если x'=xa, u'=[u\(x_i,x_j)][(x_i,a)(a,x_j)]. На рис. 3.1.8 граф G'(x',u') получен из графа G(x,u) подразделением ребра (x₂,x₄), т.е. 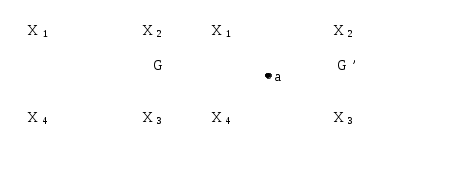, , x'=xa, u'=[u\(x_2,x₄)][(x₂,a)(a,x₄)].


Рис. 3.1.8
Два графа G₁,G₂ называются гомеоморфными, если существует такой граф G', который может быть получен как из графа G₁, так и из G₂ операцией подразделения ребра конечное число раз. Или: графы G₁ и G₂ гомеоморфны, если существуют изоморфные подразбиения G₁' и G₂'. Графы G₁ и G₂, изображенные на рис. 3.1.9, гомеоморфны.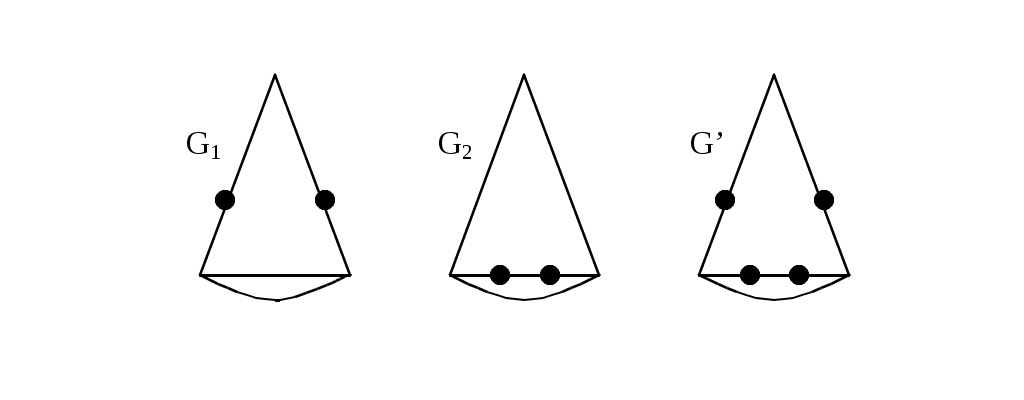

Рис. 3.1.9
Граф G' может быть получен из графов G₁ и G₂ операцией подразделения ребра, проведенной дважды.

Теорема Понтрягина-Куратовского. Граф планарен тогда и только тогда, когда он не содержит подграфа, гомеоморфного графам K₁ или K₂ (рис. 3.1.7).

Вслед за этим классическим результатом были предложены другие критерии планарности, не рассматриваемые в данном учебном пособии.

Числа, характеризующие граф
Цикломатическим числом графа называется число =N-n+p, где N- число ребер графа, n – число его вершин, P – число компонент связности. Для связного графа =N-n+1.

Теорема. Цикломатическое число графа равно наибольшему количеству независимых циклов.

Понятие независимых циклов состоит в следующем. Поставим в соответствие циклу μ графа G некоторый вектор. Для этого придадим каждому ребру графа произвольную ориентацию. Если цикл μ проходит через ребро u_k в направлении его ориентации r_k раз и в противоположном направлении S_k раз, то полагаем c^k=r_k-S_k. Вектор с¹,c²,…,c^K,…,c^N) N-мерного пространства называют вектором-циклом, соответствующим циклу μ. Циклы μ₁, μ₂,… называют независимыми, если соответствующие им векторы , ,… линейно независимы.

Следствием рассмотренной теоремы являются следующие утверждения:

1. 
   Связный граф G не имеет циклов тогда и только тогда, когда =0. Такой граф есть дерево (различные определения графа-дерева будут рассмотрены в специальном разделе 3.2).
   
2. 
   Связный граф G имеет единственный цикл тогда и только тогда, когда =1.
   

Цикломатическое число связного графа можно определить как число ребер, которое нужно удалить, чтобы граф стал деревом.

Пример.

Цикломатическое число графа, изображенного на рис. 3.1.10, равно 3.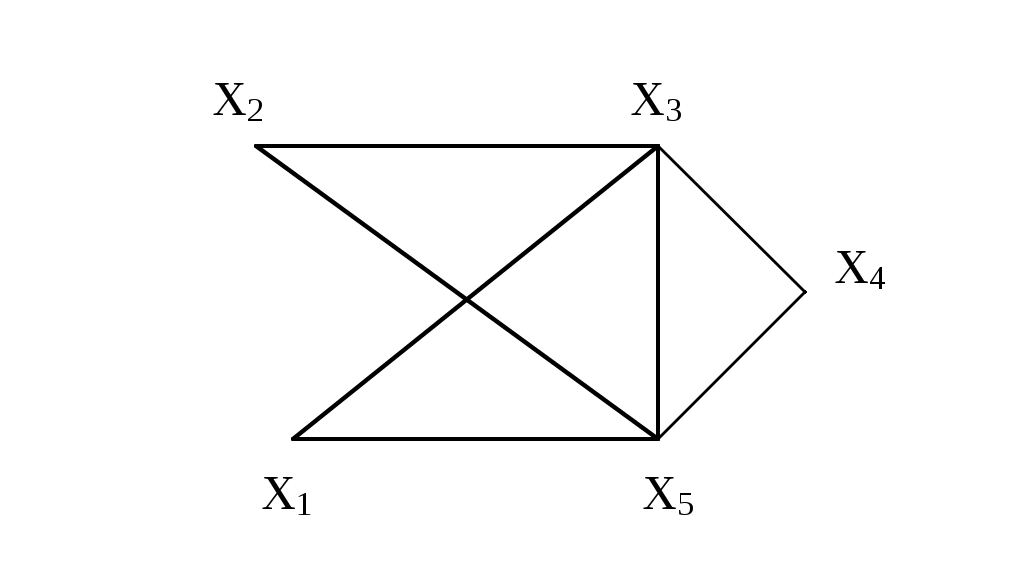



Рис. 3.1.10
Число внутренней устойчивости графа. Пусть задан некоторый граф G (x, г x). Рассмотрим такое подмножество его вершин S Х, в котором две любые точки являются несмежными. Такое подмножество S называется внутренне устойчивым. Другими словами, подмножество S Х является внутренне устойчивым, если гSS=ø.

Обозначим |S| – мощность множества S. Пусть F – множество всех внутренне устойчивых множеств. Числом внутренней устойчивости графа G называется

(G)= |S|.

Отыскание (G) нужно начинать с максимального числа вершин и, постепенно увеличивая его, проверять, образуют ли выбранные вершины внутренне устойчивое множество.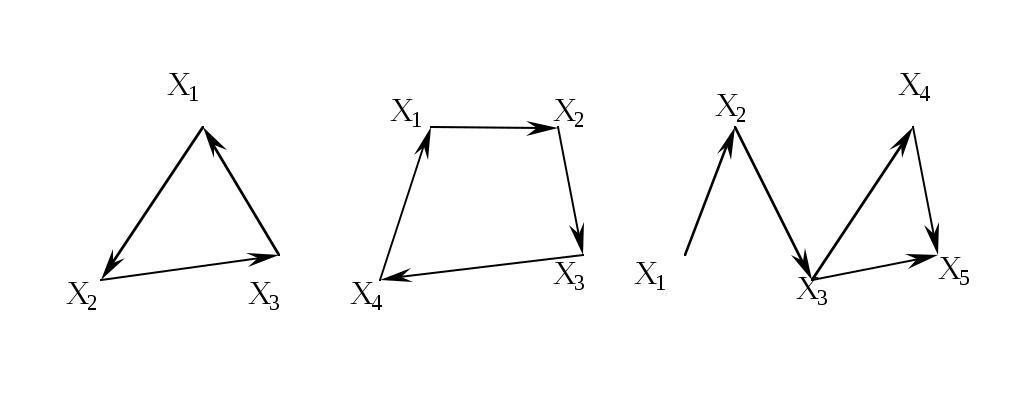



Рис. 3.1.11

Для графов, изображенных на рис. 3.1.11, имеем следующие числа внутренней устойчивости. (G₁)=1, т.к. любая пара вершин G₁ является смежной. Граф G₂ имеет два внутренне устойчивых множества S₁={x₁,x₃}, S₂={x₄,x₂}. Так как, |S₁|=|S₂|=2, то, следовательно, (G₂)=2. Граф G3 содержит внутренне устойчивые множества S₁={x₁,x₅}, S₂={x₁,x₃}, S₃={x₁,x₄}, S₄={x₂,x₅},S₅={x₂,x₄}.

Но если к любому из этих множеств добавить какую-либо вершину, не содержащуюся в нем, то подмножество перестанет быть внутренне устойчивым, следовательно, (G₃)=2.

Число внешней устойчивости графа. Пусть задан некоторый граф G(x,гx). Подмножество его вершин TХ есть внешне устойчивое множество, если для каждой точки x_i(X/T) выполнено условие

гx_iTø.

Обозначим |T| – мощность множества T. Пусть Ф – множество всех внешне устойчивых множеств. Числом внешней устойчивости графа G называется
(G)= |T|.
При подсчете числа внешней устойчивости следует начинать с максимального числа вершин графа, затем уменьшать его, проверяя, образуют ли выбранные вершины внешне устойчивое множество.
Пример.

Определим число внешней устойчивости для графов, изображенных на рис.3.1.11. Любая пара вершин графа G₁ образует внешне устойчивое множество, но любая его вершина не является внешне устойчивым множеством, следовательно, (G₁)=2. Граф G₂ содержит два внешне устойчивых множества T₁={x₁,x₃}, T₂={x₂,x₄} с минимальным числом элементов, т.е. (G₂)=2. Для графа G₃ внешне устойчивым множеством минимальной мощности является T={x₁,x₃}, т.е. (G₃)=2.

К определению числа внешней устойчивости графа сводится задача о часовых. На посту расставлены часовые, охраняющие n объектов, причем один и тот же часовой может наблюдать за несколькими объектами. Нужно выяснить, каково минимальное число часовых, необходимых для наблюдения за всеми объектами. Граф, изображенный на рис.3.1.12, соответствует следующей задаче: 9 вершин графа – охраняемые объекты (n=9), ребра характеризуют возможность просматривания объектов часовыми. Так, например, часовой у объекта X₁ может одновременно наблюдать за объектами X₂,X₃,X₄, X₉, часовой у объекта X₂ – за объектами X₁,X₃,X₇,X₈ и т.д. Для данного графа число внешней устойчивости равно 2. Внешне устойчивое множество образуют вершины X₄,X₈. Достаточно двух часовых, расположенных в точках X₄ и X₈, для охраны всех объектов.



Рис 3.1.12
Ядро графа. Если множество вершин графа G(x,гx) содержит подмножество LХ как внутренне, так и внешне устойчивое, то такое подмножество L называется ядром графа.

Обозначим |L| мощность множества L. Эта величина удовлетворяет неравенству (G)|L|(G).
Пример.

Граф G₁ (рис.3.1.11) не имеет ядра; граф G₂ имеет два ядра {x₁,x₃}, {x₂,x₄}; граф G₃ имеет одно ядро {x₁,x₃}.

Хроматическое число графа. Предположим, что каждая вершина графа G окрашена в какой-либо цвет так, что никакие две смежные вершины не окрашены одинаково. Если при этом потребовалось К красок, то граф называется хроматическим порядка К. Минимальное число К, при котором граф остается хроматическим, называется хроматическим числом и обозначается γ. Для графа G, изображенного на рис.3.1.13, хроматическое число γ(G)=3.


Рис. 3.1.13
Теорема. Для каждого графа G выполняется неравенство n(G)(G), где n=|Х| – мощность множества X, (G) – число внутренней устойчивости, (G) – хроматическое число графа.

Доказательство. Все множество вершин графа можно разбить на  внутренне устойчивых множеств, состоящих из точек одинакового цвета. Пусть внутренне устойчивые множества содержат m₁,…,m_ вершин. m_i(G), т.к. (G) по определению есть максимальное число вершин внутренне устойчивых множеств. Но n=m₁+m₂+…+m_, следовательно, n(G)(G).

Задача о раскраске геометрической карты связана с определением хроматического числа графа. Любую географическую карту можно изобразить в виде графа G(x,гx), где вершинами являются страны, а ребрами связаны страны, граничащие между собой. Такой граф является плоским. Гипотеза о четырех красках состоит в утверждении того, что граф, соответствующий любой географической карте, имеет хроматическое число не больше 4. Долгое время это предположение оставалось недоказанным, несмотря на широкий интерес математиков к этой проблеме. Благодаря созданию современных ЭВМ решение этой проблемы стало возможным, что и было проделано американскими математиками К. Аппелем и В. Хакеном. Задача была решена путем сведения ее к некоторым частным вопросам чисто арифметического характера, требующим большого числа вычислений, которые были бы не под силу человеку, не вооруженному современной вычислительной техникой.

Операции над графами. Объединение графов
Объединением графов G₁(x₁,г₁x₁) и G₂(x₂,г₂x₂) называется такой граф G(x,гx), у которого множество вершин есть сумма множеств вершин объединяемых графов x=x₁x₂, а отображение есть сумма отображений объединяемых графов гx=г₁x₁г₂x₂, что обозначается: G=G₁G₂.

Пример. Заданы графы G₁ и G₂:



Требуется определить G(x,гx)=G₁G₂.









Геометрическая реализация складываемых графов и графа-суммы имеет следующий вид (рис. 3.1.14):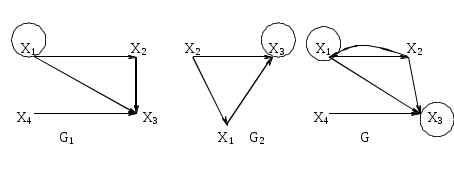



Рис. 3.1.14
Граф-сумма содержит все вершины и дуги, встречающиеся хотя бы в одном из двух складываемых графов.
Пересечение (произведение) графов
Пересечением графов G1(x₁,г₁x₁) и G2(x₂,г₂x₂) называется такой граф G(x,гx), у которого множество вершин есть пересечение множеств вершин графов X=X₁X₂, а отображение есть пересечение отображений перемножаемых графов ГX=Г₁X₁Г₂X₂.

Пример.

Пересечение графов G₁ и G₂ предыдущего примера есть граф G(x,гx) (геометрическая реализация на рис 3.1.15):

Рис. 3.1.15

Граф-пересечение содержит вершины и дуги, являющиеся общими у перемножаемых графов.

Прямое произведение графов
Прямым (декартовым) произведением графов G₁(x₁,г₁x₁) и G₂(x₂,г₂x₂) называется граф G(x,гx), для которого X=X₁ X₂ и гx=г₁x₁ г₂x₂.

Пример.

Найти декартово произведение графов G₁ и G₂ (рис. 3.1.16):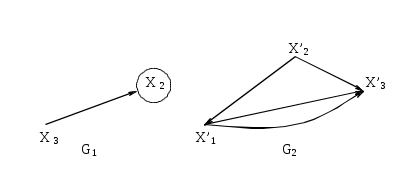



Рис. 3.1.16.






Обозначим каждую получившуюся вершину через , тогда















Геометрическая реализация графа G имеет вид (рис. 3.1.17):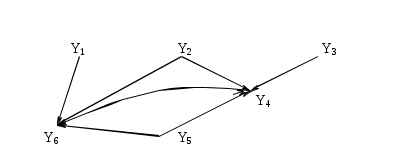

Рис. 3.1.17

Матрицы для графов
Матрицей смежности данного графа G(x,гx) называется квадратная матрица порядка n, где n – мощность множества X, элемент которой определяется следующим образом:
a_ij =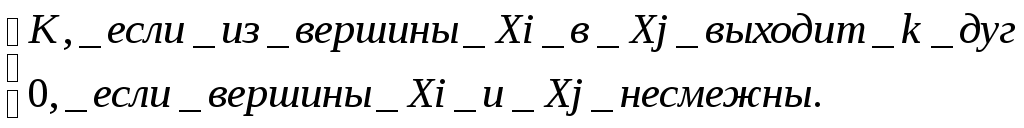
Для графа, две вершины которого соединены не более чем одной дугой одного направления, матрица смежности состоит из единиц и нулей (K=1). В дальнейшем будем рассматривать только такие графы.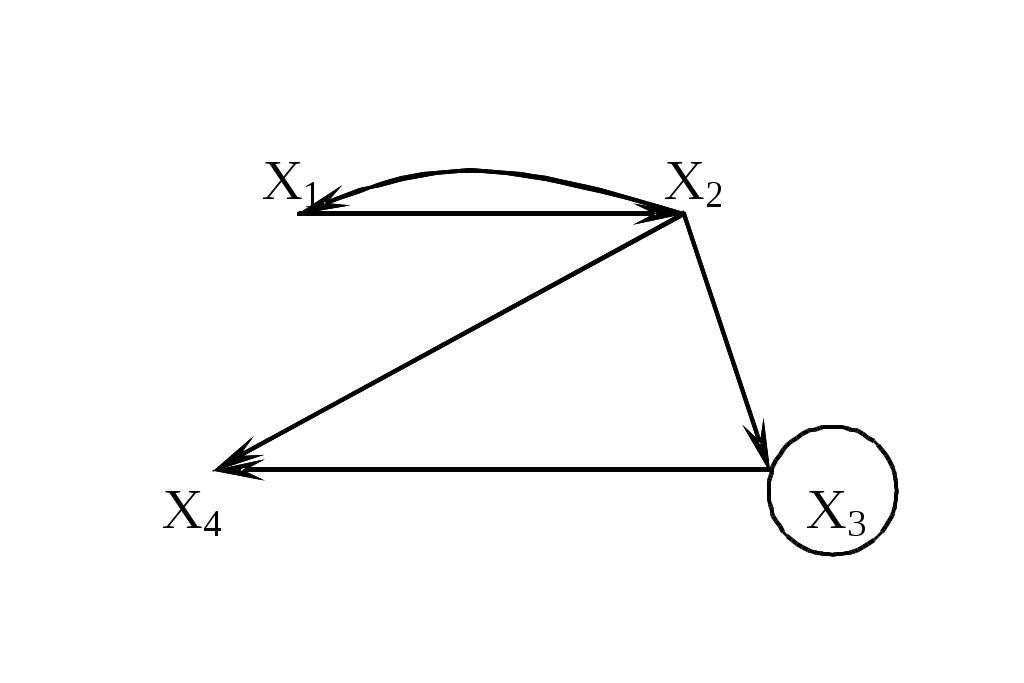


Рис. 3.1.18

Пример.

Граф, изображенный на рис. 3.1.18, имеет следующую матрицу смежности: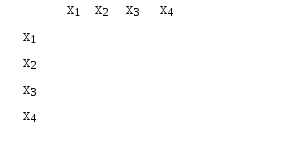


Полустепень исхода вершины x_i равна числу единиц, стоящих в i-й строке. Полустепень захода равна числу единиц, стоящих в i-м столбце. Найдя сумму полустепеней i-й вершины, можем определить ее степень по матрице смежности. Так,

P(x₂)=P⁺+P^-=1+3=4

Единицы, стоящие на главной диагонали матрицы смежности, соответствуют петлям при данной вершине.

Изолированной вершине соответствуют строка и столбец, состоящие из нулей.

Число единиц в матрице смежности равно числу дуг графа.

Транспонированной матрице смежности соответствует граф с противоположной ориентацией.

Матрица смежности полностью задает ориентированный граф. Любая квадратная матрица, состоящая из единиц и нулей, может быть рассмотрена как матрица смежности, задающая некоторый граф G.

Рис. 3.1.19

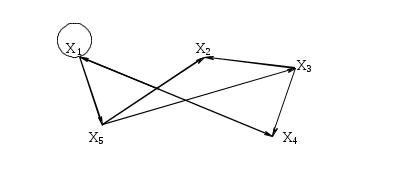
Так, матрице M и соответствует граф, изображенный на рис.3.1.19.

Операции над графами с помощью матриц смежности. Если следует найти объединение или пересечение графов, заданных их матрицами смежности, можно выполнить эти операции, не прибегая к аналитической записи графа или его геометрической реализации.
Пример.

Напишем матрицы смежности A и B графов G₁ и G₂ (рис.3.1.14), над которыми произведем операции сложения и умножения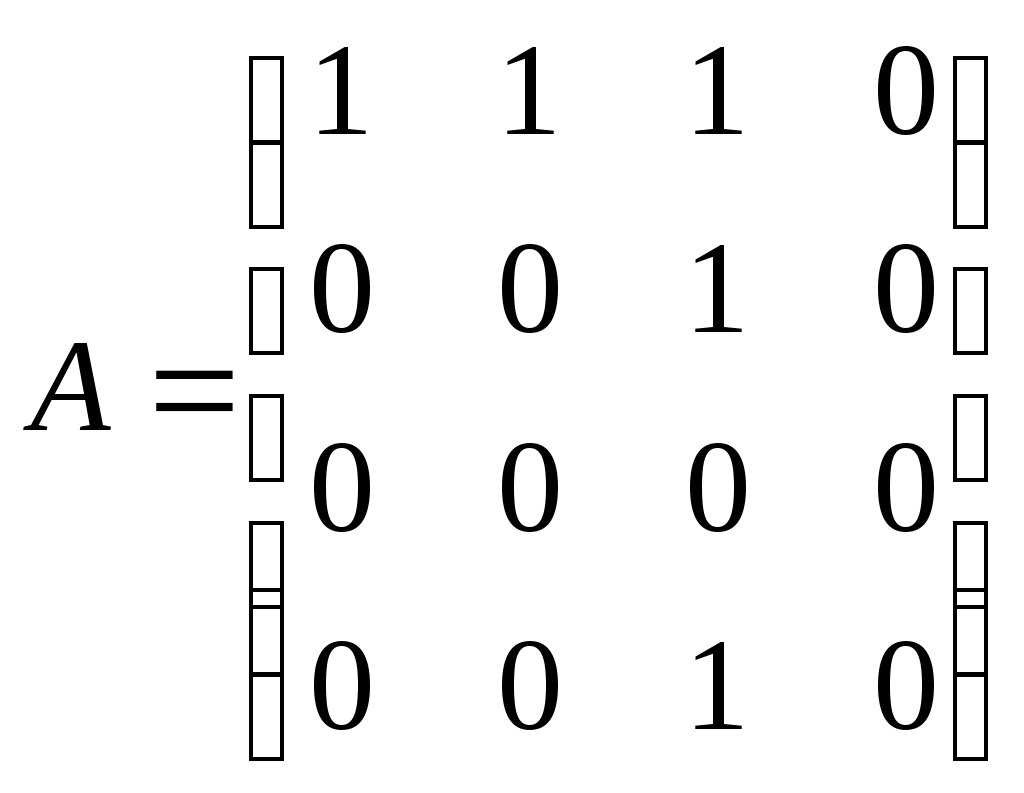
,
а также матрицы смежности С и D для графа, являющихся их объединением (рис. 3.1.15) и пересечением (рис. 3.1.16)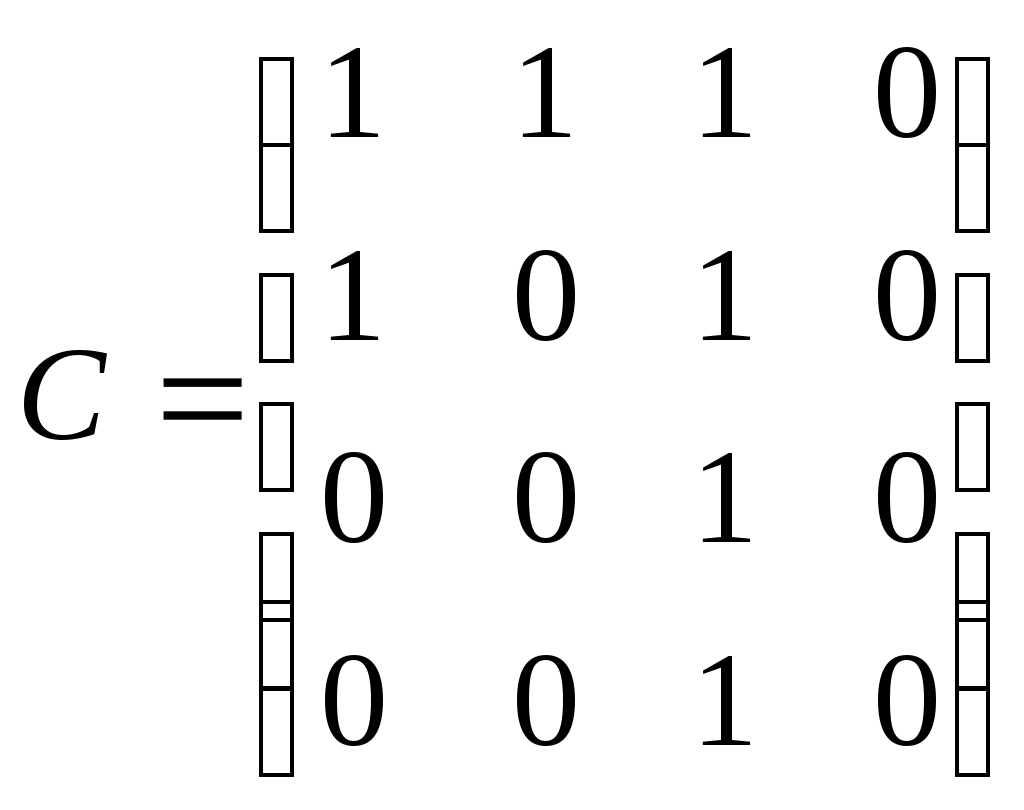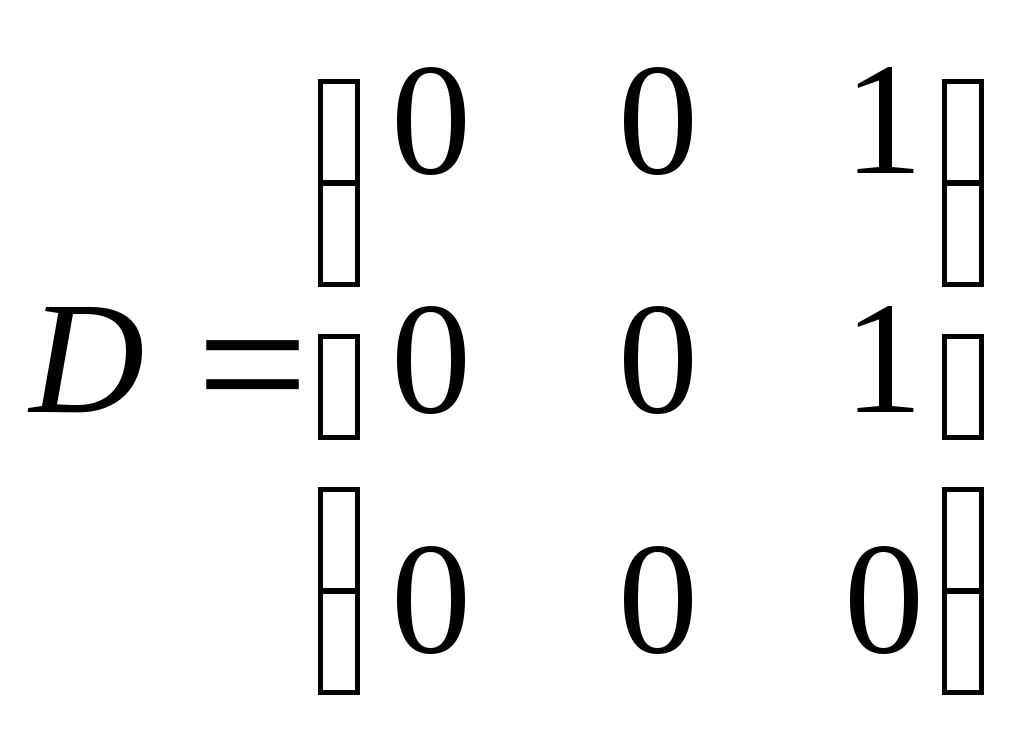
,
Рассмотренный пример иллюстрирует то обстоятельство, что матрица смежности для графа суммы есть булева сумма матриц смежности складываемых графов: c_ij=a_ij+b_ij, причем 0+0=0; 0+1=1; 1+0=1; 1+1=1.

Матрица смежности для графа-пересечения может быть получена поэлементным умножением d_ij=a_ij+b_ij, причем 0 1=0; 1 0=0; 0 0=0; 1 1=1, т.е. матрица смежности графа-пересечения содержит единицы только в качестве тех элементов, которые равны единицам в обеих матрицах смежности перемножаемых графов.

Матрица инциденций
Матрицей инциденций ориентированного графа G (x, u) называется прямоугольная матрица порядка [n * m], где n – мощность множества X, m – мощность множества U, каждый элемент которого a_ij определяется следующим образом:

	если xi – начало дуги ui
	если xi – конец дуги ui
	если xi – не инцидентна дуге ui

Пример.

Напишем матрицу инциденций для графа, изображенного на рис. 3.1.20.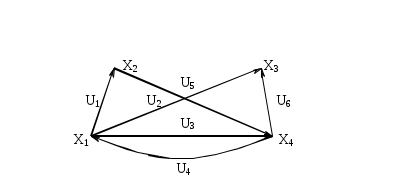

Рис. 3.1.20
Для этого пронумеруем дуги: u₁,u₂,…,u₆, матрица инциденций будет иметь следующий вид: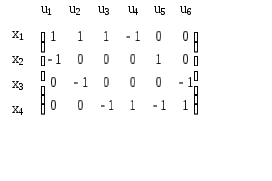