Анализ временных рядов и прогнозирование. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
 Скачать 2.56 Mb. Скачать 2.56 Mb.
|
3.2. Простейшие методы прогнозной экстраполяцииНаиболее простыми методами прогнозирования по одномерным временным рядам, являются:
Рассмотрим каждый из названных методов. Прогнозирование в предположении абсолютной неизменности значений предшествующих уровней исходит из утверждения, что каждое следующее прогнозное значение будет равно предыдущему значению признака, то есть: 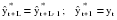 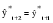 (3.2) (3.2)где: 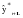 – прогнозное значение на период упреждения L. – прогнозное значение на период упреждения L.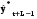 – прогнозное значение, предшествующее периоду упреждения L. – прогнозное значение, предшествующее периоду упреждения L.Данный случай прогнозирования является частным и в практике статистического прогнозирования социально-экономических явлений встречается крайне редко. Другим простейшим методом прогнозирования социально-экономических явлений является метод прогнозирования на основе среднего уровня ряда. Данный метод прогнозирования используется для случаев, когда изменение значений уровней временных рядов носит стационарный характер. При построении прогноза данным методом используется принцип, согласно которому значения всех последующих прогнозируемых уровней принимаются равными среднему значению уровней ряда в прошлом, то есть: 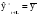 , (3.3) , (3.3)Таким образом получают точечный прогноз. Однако, рассматривая временный ряд как выборку из некоторой генеральной совокупности, сложно предположить, что прогнозная точечная оценка полностью совпадает с эмпирическими значениями признака. В этом случае целесообразно определить доверительный интервал прогноза путем построения интервального прогноза данным методом по выражению вида: 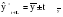 , (3.4) , (3.4)где: t – табличное значение; t – критерий Стьюдента с (n-1)числом степеней свободы и уровнем значимости; 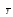 –средняя квадратическая ошибка средней, которая определяется по формуле: –средняя квадратическая ошибка средней, которая определяется по формуле: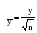 , (3.5) , (3.5)где: σy– среднее квадратическое отклонение, которое определяется как: 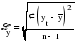 , (3.6) , (3.6)где: 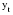 – эмпирические значения уровней временного ряда; – эмпирические значения уровней временного ряда;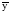 – средний уровень исходного временного ряда; – средний уровень исходного временного ряда;n– число уровней ряда. Полученный таким образом (3.4) доверительный интервал учитывает колеблемость выборочных средних и предполагает, что каждая следующая прогнозная оценка будет равна среднему уровню ряда динамики. При этом упускается из вида возможность колеблемости эмпирических значений признака вокруг средней, то есть в определении доверительного интервала. В расчете дисперсии необходимо учесть как колеблемость выборочных средних, так и степень варьирования индивидуальных эмпирических значений признака вокруг средней. В этом случае доверительный интервал прогнозной оценки можно определить по выражению вида: 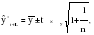 (3.7) (3.7)Как видно, общая вариация прогнозируемого социально-экономического явления, то есть его ошибка, определяется суммой двух дисперсий: общая дисперсия и дисперсия выборочной средней при условии рассмотрения исходного временного ряда как выборки из некоторой генеральной совокупности. Прогнозирование методом среднего абсолютного прироста предполагает, что общая тенденция развития изучаемого социально-экономического явления наилучшим образом аппроксимируется линейной формой аналитического выражения. Применение данного метода прогнозирования возможно при предварительной проверке следующих предпосылок:
где: yt – значение уровня t-го периода; yt-1 – значение уровня предшествующего t-му периоду времени) должны быть приблизительно одинаковыми;
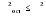 , ,где: 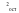 – остаточная дисперсия, определяемая по формуле: – остаточная дисперсия, определяемая по формуле: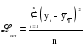 , (3.8) , (3.8)где: yt– эмпирические значения уровней временного ряда; 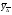 – теоретические значения уровней ряда, выровненные методом среднего абсолютного прироста; – теоретические значения уровней ряда, выровненные методом среднего абсолютного прироста;n– число уровней исходного временного ряда. 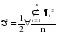 , (3.9) , (3.9)где: t – цепные абсолютные приросты уровней исходного временного ряда. После проверки и подтверждения выполнения данной предпосылки можно приступать к прогнозированию методом среднего абсолютного прироста, общая модель прогноза которого имеет вид: 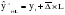 , (3.10) , (3.10)где: yt – последний уровень исходного временного ряда (для перспективного прогноза) или уровень принятый за базу экстраполяции; L– период упреждения прогноза; 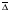 – средний абсолютный прирост, который определяется по формулам вида: – средний абсолютный прирост, который определяется по формулам вида: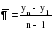 или или 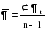 , (3.11) , (3.11)где: 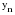 – последний уровень исходного временного ряда; – последний уровень исходного временного ряда;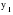 – первый уровень исходного временного ряда. – первый уровень исходного временного ряда.Как видно из приведенных преобразований, прогнозирование методом среднего абсолютного прироста заключается в непрерывном увеличении последнего уровня исходного ряда динамики на величину среднего абсолютного прироста на всем периоде упреждения. Пример. По следующим данным об объеме ипотечного кредитования коммерческой недвижимости в одном из регионов РФ за период январь-август 2009 г. построить прогноз методом среднего абсолютного прироста на сентябрь – ноябрь 2009 г. (таблица 3.1). Таблица 3.1 Расчетная таблица для определения прогнозных значений методом среднего абсолютного прироста
Средний абсолютный прирост составил: 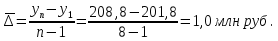 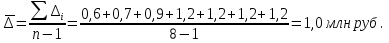 Проверим неравенство: 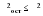 . .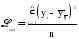 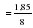 = 0,231; = 0,231;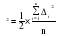 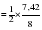 = 0,464, = 0,464,следовательно, основная предпосылка выполняется, что свидетельствует о том, что данным методом можно прогнозировать объем ипотечного кредитования. Прогнозные оценки данного показателя на сентябрь – ноябрь 2009 г. составят: 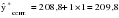 млн. руб. млн. руб.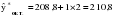 млн. руб. млн. руб.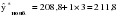 млн. руб. млн. руб.Прогнозирование методом среднего темпа роста осуществляется в случае если темпы роста цепные, рассчитанные по данным исходного временного ряда за исследуемый период времени, имеют приблизительно одинаковое цифровое значение, а тенденция развития явления подчиняется геометрической прогрессии и может быть описана показательной (экспоненциальной) кривой. Модель прогноза методом среднего темпа роста имеет вид: 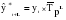 , (3.12) , (3.12)где: 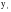 – последний уровень исходного временного ряда (для перспективного прогноза) или уровень принятый за базу экстраполяции (во всех остальных случаях); – последний уровень исходного временного ряда (для перспективного прогноза) или уровень принятый за базу экстраполяции (во всех остальных случаях);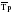 – средний темп роста, который определяется по формулам вида: – средний темп роста, который определяется по формулам вида: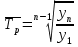 или или (3.13) (3.13)где: 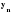 – последний уровень исходного временного ряда; – последний уровень исходного временного ряда;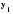 – первый уровень исходного временного ряда; – первый уровень исходного временного ряда;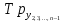 – цепные темпы роста; – цепные темпы роста;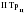 – произведение цепных темпов роста – произведение цепных темпов ростаСумма теоретических значений 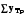 , полученных в результате выравнивания по среднему темпу роста, должна совпадать с суммой эмпирических значений исходного временного ряда , полученных в результате выравнивания по среднему темпу роста, должна совпадать с суммой эмпирических значений исходного временного ряда 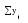 : :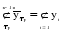 , (3.14) , (3.14)Несовпадение данных сумм может быть вызвано следующими причинами:
Пример. По следующим данным об объеме товарооборота по торговым точкам города в январе-мае 2009 г. постройте прогноз на июнь-июль 2009 г. методом среднего темпа роста (таблица 3.2). Таблица 3.2 Расчетная таблица для определения прогнозных значений методом среднего темпа роста
Средний темп роста составил: 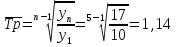 или  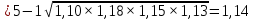 Прогноз объема товарооборота по торговым точкам города составил: 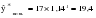 млн. руб. млн. руб.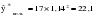 млн. руб. млн. руб.Рассмотренные методы прогнозирования являются простейшими, и поэтому прогнозы, полученные на их основе, являются приближенными и не всегда надежны при увеличении периода упреждения. Как правило, эти методы используются только при краткосрочном прогнозировании. Применение этих методов в среднесрочном и долгосрочном прогнозировании нецелесообразно, так как они не только не учитывают вариацию, скачки внутри временного ряда, но и в основе построения моделей прогноза и получения прогнозных оценок на всем периоде упреждения лежит принцип равномерного увеличения или уменьшения (в зависимости от знака абсолютного прироста или допустимых границ темпа роста) исследуемого явления, в частности его последнего уровня в исходном временном ряду, от одного периода упреждения к другому на постоянную величину, количественно выраженную значением среднего абсолютного прироста или среднего темпа роста. 3.3. Прогнозирование на основе экстраполяции тренда Наиболее распространенным методом прогнозирования выступает аналитическое выражение тренда. При этом, для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной – времени. При таком подходе к прогнозированию предполагается, что размер уровня, характеризующего явление, формируется под воздействием множества факторов, причем не представляется возможным выделить порознь их влияние. В связи с этим ход развития связывается не с какими-либо конкретными факторами, а с течением времени, то есть: 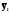 = f (t), (3.15) = f (t), (3.15)Экстраполяция дает возможность получить точечное значение прогноза. Точечный прогноз есть оценка прогнозируемого показателя в точке (в конкретном году, месяце, дне) по уравнению, описывающему тенденцию показателя. Точечная оценка рассчитывается путем подстановки номера года t, на который рассчитывается прогноз, в уравнение тренда. Она является средней оценкой для прогнозируемого интервала времени. Совпадение фактических данных и прогностических оценок – явление маловероятное, поэтому целесообразно определить доверительные интервалы прогноза. Величина доверительного интервала определяется следующим образом: 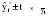 , (3.16) , (3.16)где: 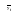 – средняя квадратическая ошибка тренда; – средняя квадратическая ошибка тренда;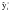 – расчетное прогнозное значение уровня; – расчетное прогнозное значение уровня;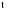 – доверительное значение критерия Стьюдента. – доверительное значение критерия Стьюдента.Метод прогнозирования на основе экстраполяции тренда базируется на следующих предпосылках:
Трендовые модели выражаются различными функциями 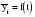 , на основе которых строятся модели прогноза и осуществляется их оценка. , на основе которых строятся модели прогноза и осуществляется их оценка.На практике наибольшее распространение получили следующие виды трендовых моделей:
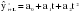 ; ;
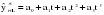 и т.д. и т.д.
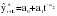
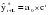 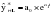
При этом наиболее существенным вопросом прогнозирования по трендовым моделям является проблема точного прогноза. Точная оценка прогноза весьма условна в силу следующих причин:
Рассматривая получение интервальных или точечных оценок прогноза следует учитывать, что в отдельных случаях получение более точных оценок не гарантирует надежности прогноза. Применение трендовых моделей прогнозирования социально-экономических явлений имеет большую значимость и, несмотря на определенную простоту их реализации, часто используются для прогнозирования сложных социально-эконо-мических явлений. Если выбранная модель тренда достаточно правильно отражает тенденцию развития, то полученные на ее основе прогнозы практически всегда надежны. Прогнозирование методом экстраполяции тренда основывается на анализе тенденций развития одномерных временных рядов социально-экономических явлений и процессов. Однако прогноз по аналитическому выражению тренда имеет один существенный недостаток, который иногда приводит к большим ошибкам при прогнозировании явления. Дело заключается в том, что в данном случае прогнозируется только детерминированная составляющая ряда динамики и не учитывается случайный компонент. Чтобы избежать этой ошибки и сделать прогноз более точным, надо отыскать закономерность изменения во времени случайного компонента. Для этого принято вначале находить отклонения от тренда и определять закономерность их изменения во времени, а затем делать прогноз случайной составляющей динамического ряда. Результаты обоих прогнозов объединяются. Рассматриваемый метод тогда дает удовлетворительные результаты, когда в эмпирическом ряду случайные колебания будут небольшими и между ними отсутствует автокорреляция. |

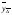
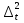
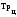
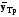
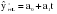 ;
;
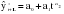
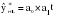 , (3.17)
, (3.17)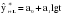 .
.