Анализ временных рядов и прогнозирование. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
 Скачать 2.56 Mb. Скачать 2.56 Mb.
|
Таблица 2.19Расчетная таблица для определения параметров критерия серий, основанного на медиане выборки, для моделей линейного тренда и параболы второго порядка, описывающих тенденцию в изменении объема платных услуг населению одного из регионов РФ за январь–декабрь 2009 г.
1. Произведем оценку случайности отклонений эмпирических значений объема платных услуг населению от теоретических, полученных на основе линейного тренда: 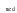 = = 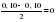 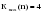 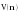 = 6 = 6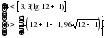 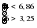 . .Оба приведенных неравенства выполняются одновременно, следовательно гипотеза о случайности отклонений эмпирических уровней временного ряда объема платных услуг населению от теоретических, полученных по уравнению линейного тренда не отвергается. 2. Произведем оценку случайности отклонений эмпирических значений объема платных услуг населению от теоретических, полученных на основе параболы второго порядка: 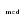 = = 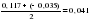 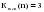 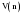 = 7 = 7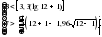 ; ;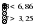 . .Вывод аналогичен, то есть оба приведенных неравенства выполняются одновременно, следовательно гипотеза о случайности отклонений эмпирических уровней временного ряда объема платных услуг населению от теоретических, полученных по уравнению параболы второго порядка не отвергается. Критерий «восходящих» и «нисходящих» серий. Этапы реализации метода:
t+1 > t – «+» t+1 < t – «-» t+1 = t – учитывается только одно наблюдение (другие опускаются).
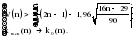 ; (2.38) ; (2.38)где: k0(n) – определяется следующим образом:
Если хотя бы одно из неравенств не выполняется, то гипотеза о случайном характере отклонений уровней временного ряда от тренда отвергается. Пример. Произведем оценку случайности отклонений эмпирических значений числа зарегистрированных разбоев в РФ от теоретических, полученных по уравнениям линейного тренда и параболы второго порядка. 1. В качестве примера рассмотрим отклонения от линейного тренда. Расчет параметров линейного тренда был произведен ранее и получено уравнение тренда: 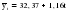 . .Определим отклонения эмпирических значений признака от теоретических, полученных по уравнению тренда. Последовательно сравним каждое следующее значение εt с предыдущим:
Результат отразим в таблице. Таблица 2.20 Расчетная таблица критерия «восходящих» и «нисходящих» серий (по отклонениям от линейного тренда)
Выдвигается гипотеза H0 : о случайности отклонений в ряду динамики. Для проверки выдвинутой гипотезы определим:
Гипотеза не отвергается, если справедлива следующая система неравенств: 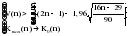 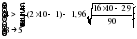 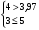 . .Оба неравенства выполняются, следовательно гипотеза о случайности отклонений уровней ряда динамики числа зарегистрированных разбоев в РФ от линейного тренда 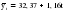 не отвергается. не отвергается.
Расчет параметров параболы был произведен ранее и получено уравнение тренда 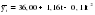 . .Последовательно сравним каждое следующее значение εt с предыдущим:
Таблица 2.21 Расчетная таблица критерия «восходящих» и «нисходящих» серий (по отклонениям от параболы второго порядка)
Выдвигается гипотеза H0: о случайности отклонений эмпирических значений числа зарегистрированных разбоев от теоретических, полученных по уравнению второго порядка. Для проверки выдвинутой гипотезы определим: – длину наибольшей серии 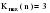 ; ;– число серий V(n)=6; – при n<=26 K0(n)=5. Гипотеза не отвергается, если справедлива следующая система неравенств. 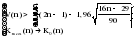 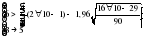 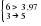 . .Оба неравенства выполняются, гипотеза о случайности отклонений уровней ряда динамики от параболы второго порядка 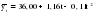 не отвергается. не отвергается.Критерий восходящих и нисходящих серий показал случайность отклонений уровней временного ряда от тренда в виде прямой и в виде параболы. 2.6. Модели периодических колебаний При рассмотрении квартальных и месячных данных часто обнаруживаются периодические колебания, вызываемые сменой времен года. Их называют сезонными. Изучение сезонных колебаний имеет самостоятельное значение как исследование особого типа динамики. Сезонность можно понимать как внутригодовую динамику вообще. Во многих случаях сезонность приносит ущерб экономике в связи с неравномерным использованием оборудования и рабочей силы, с неравномерной нагрузкой транспорта, поставкой сырья для других отраслей, связанных с сезонными отраслями. Выявление сезонной составляющей может быть произведено на основе следующих методов, примеры на которые приведены ниже (таблицы 2.22 и 2.23). I. Метод абсолютных разностей (таблица 2.22):
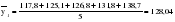 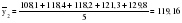 - определяется среднемесячный уровень для пятилетки: 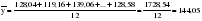
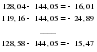 . .II. Метод отношений помесячных средних ( 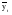 ) ) к средней за весь период (таблица 2.22): 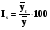 , – индекс сезонности (2.39) , – индекс сезонности (2.39)где: 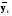 – средняя для каждого месяца – средняя для каждого месяца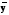 – общий среднемесячный уровень за весь период. – общий среднемесячный уровень за весь период.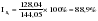 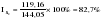 … 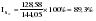 III. Метод отношений помесячных уровней к средней месячной данного года (таблица 2.22):
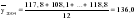 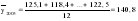
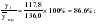 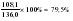 ; ;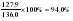 . .
Январь 86,6 + 88,8 + 88,8 + 89,3 + 90,7 = 444,2 Февраль 79,5 + 84,1 + 82,8 + 82,2 + 84,8 = 413,4 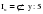 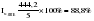 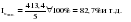 2004 2005 2006 2008 2007 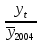 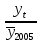 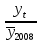 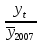 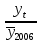 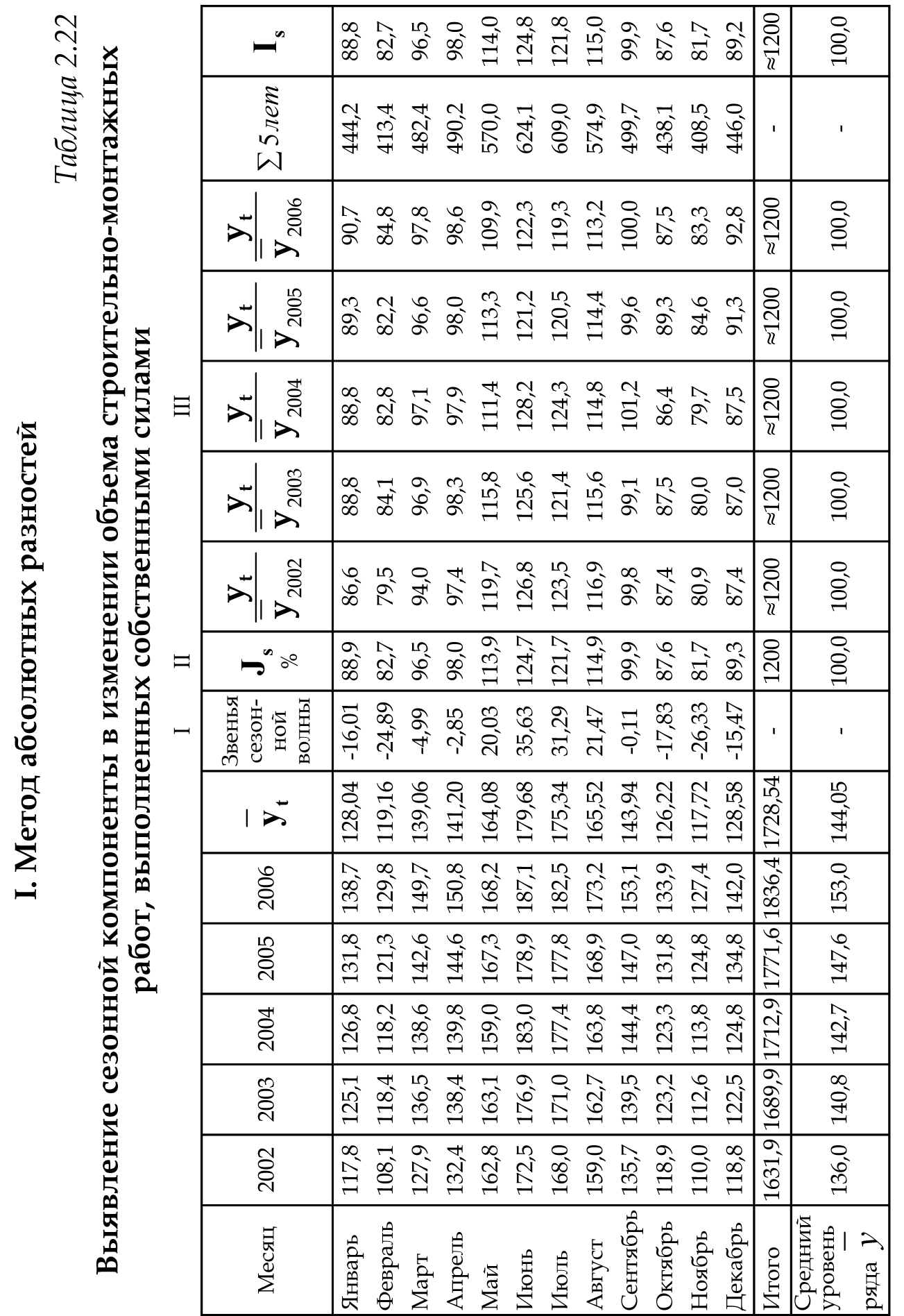 IV. Метод относительных величин (таблица 2.23).
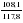 ; ; 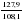 ; ; 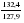 ; …; ; …; 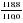 . .
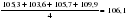 ; ;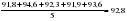
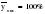 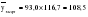 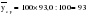 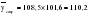 и … и …
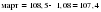 . .
IV. Метод относительных величин на основе медианы (таблица 2.23):
определяется Ме : 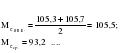 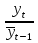 2008 % 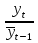 2007 % 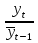 2006 % 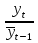 2005 % 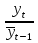 2004 % 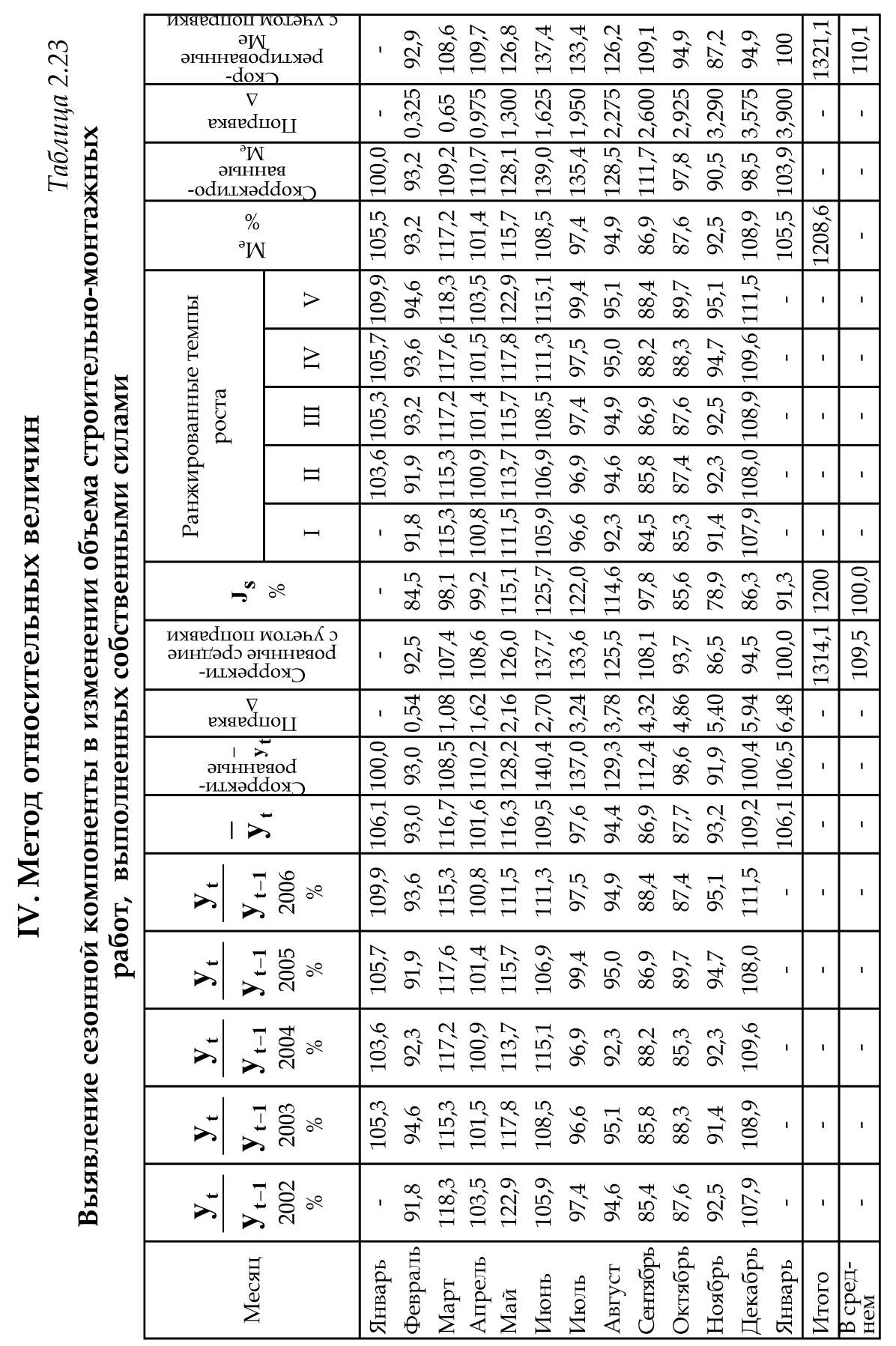 V. Метод относительных величин на основе медианы (таблица 2.23):
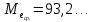
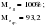 ; ;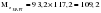 ; ;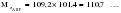
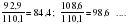 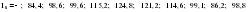 Итого =1200,00 или 100,0 – средняя. Можно построить модель сезонной волны и численно определить размах сезонных колебаний, характер их проявления в различных отраслях народного хозяйства. Моделью периодически изменяющихся уровней служит ряд Фурье: 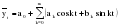 , (2.39) , (2.39)где: k – определяет номер гармоники ряда Фурье и может быть взята с разной степенью точности (чаще от «1» до «4»). Параметры уравнения определяются методом наименьших квадратов, то есть по условию 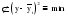 . Решая систему нормальных уравнений, получим: . Решая систему нормальных уравнений, получим: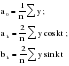 . (2.40) . (2.40)Для изучения сезонности берется (n = 12) по числу месяцев в году. Как правило, при выравнивании по ряду Фурье рассчитывают не более четырех гармоник и затем уже определяют, какая гармоника наилучшим образом отражает периодичность изменения уровней ряда. Так, при k=1: 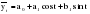 ; ;k=2: 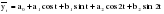 . (2.41) . (2.41)Рассчитав остаточные дисперсии 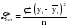 для 2-х случаев, можно сделать вывод, какая гармоника Фурье наиболее близка к фактическим уровням ряда. для 2-х случаев, можно сделать вывод, какая гармоника Фурье наиболее близка к фактическим уровням ряда.Моделирование сезонности проводится в следующей последовательности: 1. Определяется тенденция исходного ряда динамики и ее аналитическое выражение, например, в виде линейного тренда: 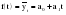 . .Например, предположим, что динамика объема строительно-монтажных работ, выполненных собственными силами, наилучшим образом описывается уравнением следующего вида: 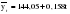 . .2. Определяются 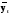 – теоретические уровни ряда динамики; – теоретические уровни ряда динамики;3. Определяется ( 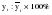 ) – по месяцам года. ) – по месяцам года.4. Определяются средние арифметические по месяцам года. Получается ряд индексов, характеризующих сезонную волну. 5. Определяется модель сезонной волны: 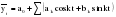 – ряд Фурье. – ряд Фурье.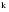 – порядковый номер гармонии. – порядковый номер гармонии. 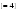 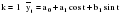 (2.42) (2.42)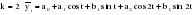 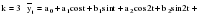 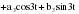 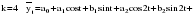 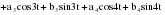 Таблица 2.24 Множители гармонического анализа n=12 для расчета коэффициентов 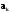 и и 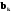
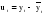 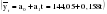 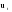 – остатки от линейной тенденции. – остатки от линейной тенденции.N=60 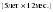 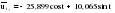 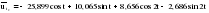 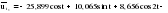 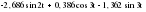 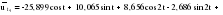 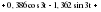 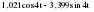 Таблица 2.25 Распределение дисперсии между гармониками
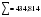 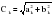 (2.43) (2.43)Вклад в дисперсию 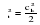 Дисперсия общая: 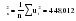 Вклад отдельный: 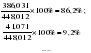 Модель имеет вид: ŷ 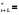 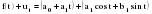 ŷ 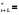 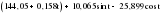 . .2.7. Модели связных временных рядов Метод наименьших квадратов, используемый в регрессионном анализе для определения коэффициентов регрессии, основывается на предпосылке независимости друг от друга отдельных наблюдений одной и той же переменной. В динамических же рядах существует еще и автокорреляция. Поэтому величины коэффициентов регрессии, полученных по способу наименьших квадратов, не имеют нужных статистических свойств. Наличие автокорреляции приводит к искажению средних квадратических ошибок коэффициентов регрессии, что в свою очередь затрудняет построение доверительных интервалов по ним и проверку их значимости по соответствующим критериям. Автокорреляция также может привести к сокращению числа наблюдений ввиду невозможности потерять показатели одного и того же объекта за ряд лет, поскольку наблюдение одного объекта за десять лет качественно отличается от наблюдений десяти объектов за одно и то же время. Возникает автокорреляция и в отклонениях от трендов, а также в случайных остатках уравнений регрессии, построенных по многомерным рядам динамики. Автокорреляция – это наличие сильной корреляционной зависимости между последовательными уровнями временного ряда. Автокорреляция может быть следствием следующих причин:
Прежде чем делать вывод о тесноте связи между рассматриваемыми рядами динамики, необходимо проверить наличие автокорреляции в них, чтобы оценить степень зависимости между соседними уровнями временного ряда. Наличие автокорреляции устанавливается с помощью коэффициента автокорреляции, который определяется на основе формулы коэффициента корреляции для парной (линейной) связи между уровнями исходного ряда и того же ряда, но сдвинутого на шагов во времени: 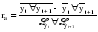 , (2.44) , (2.44)где: yt – эмпирические значения уровней ряда; yt+1 – эмпирические значения уровней, сдвинутые на один период времени ( = 1). Возникает проблема заполнения последнего уровня ряда yt+1. В данном случае возможны два варианта:
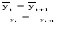 (2.45) (2.45)И коэффициент автокорреляции будет равен: 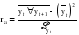 (2.46) (2.46)где: 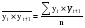 (2.47) (2.47)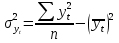 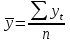 (2.48) (2.48)Затем аналогично рассчитывается коэффициент автокорреляции для всех временных рядов, входящих в связный. Если ra > ra кр при заданном уровне значимости и n, то в исходном временном ряду существует автокорреляция, в противном случае она отсутствует. Последовательность значений коэффициентов автокорреляции r, вычисленных при = 1, 2, ..., l, называют автокорреляционной функцией. Эта функция дает представление о внутренней структуре изучаемого экономического явления. Для проверки автокорреляции в уровнях ряда также используется критерий Дарбина-Уотсона. Гипотеза о наличии автокорреляции проверяется с помощью случайной величины: 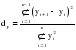 (2.49) (2.49)0 d 4. Если автокорреляции в ряду нет, то значения критерия d колеблются вокруг 2. Эмпирическое значение d сравнивается с табличным значением. В таблице есть два значения критерия – d1 и d2, v и n, где: d1 и d2 – нижняя и верхняя границы теоретических значений; v – число факторов в модели; n – число членов временного ряда. Если 1) d < d1 – в ряду есть автокорреляция; 2) d > d2 – автокорреляции нет; 3) d1 d d2 – необходимо дальше исследовать автокорреляцию. Иногда приходится при анализе рядов динамики исследовать вопрос о наличии или отсутствии автокорреляции не между самими уровнями ряда, а между их отклонениями от среднего уровня или от выровненного уровня. При значении ra 0,3 необходимо проверять наличие автокорреляции в остатках с помощью коэффициента Дарбина-Уотсона для остаточных величин: 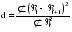 , (2.50) , (2.50)где: t – отклонения эмпирических значений уровней от теоретических, полученных по уравнению тренда. Существует теоретическое распределение значений dp для положительной автокорреляции с вероятностью 0,95, где: d1 и d2 – нижняя и верхняя границы теоретических значений; – число факторов в модели; N – число членов временного ряда. При применении критерия Дарбина-Уотсона расчетное значение dp сравнивается с табличными d1 и d2. При этом возникает три исхода:
Возможные значения критерия находятся в пределах 0 d 4. Они различны для положительной и отрицательной автокорреляции. Так как при отрицательной автокорреляции d [2; 4], для проверки следует определять величину (4 – d). Если в рядах динамики или в остаточных величинах имеется автокорреляция, то оценки коэффициентов регрессии, полученные методом наименьших квадратов, будут несмещенными, но неэффективными, так как наличие автокорреляции увеличивает дисперсии коэффициентов регрессии. Это затрудняет построение доверительных интервалов для коэффициентов регрессии и проверку их значимости. Из этого следует сделать вывод, что прежде чем проводить корреляционно-регрессионый анализ временных рядов, необходимо исключить из исследуемых рядов автокорреляцию. После того как установлено наличие автокорреляции следует приступить к построению модели. Основными моделями связных рядов динамики являются модели авторегрессии. В настоящее время разработано четыре способа исключения автокорреляции:
Модель данным методом имеет вид: yt+1 = a0 + a1x1, t+1 + a2x2, t+1 + ... + akxk, t+1. (2.51) Сущность метода заключается в последовательном исключении величины предшествующих уровней из последующих: x = xt – xt-1 y1 = yt – yt – 1 y = yt – yt-1 . . . (2.52) x1 = xt – xt – 1 x2 = xt – 1 – xt – 2 При коррелировании разностей измеряется теснота связи между разностями последовательных величин уровней в каждом динамическом ряду. Показателем тесноты связей между изучаемыми рядами является коэффициент корреляции разностей: 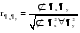 . (2.53) . (2.53)2. По отклонениям эмпирических значений от выравненных по тренду Определяется тенденция исходных рядов динамики. Рассчитывается тренд, и его величина исключается из каждого уровня. Модель в общем виде может быть представлена следующим образом: 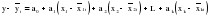 . (2.54) . (2.54)При коррелировании отклонений фактических уровней от выравненных необходимо:
Коэффициент корреляции отклонений определяется по формуле: 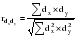 , (2.55) , (2.55)где: 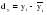 (2.56) (2.56)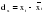 . .Коэффициент корреляции отклонений характеризует степень тесноты связи между отклонениями фактических уровней сравниваемых рядов от соответствующих им выравненных уровней коррелируемых рядов динамики. 3. Метод Фриша-Воу Этот метод заключается в ведении времени как дополнительного факторного признака. Это возможно только в случае, если основные тенденции временных рядов одинаковы. В этом случае парные связи обращаются в связи многофакторные и расчеты коэффициента корреляции и уравнения регрессии проводятся методами многофакторной корреляции и регрессии. Коэффициент корреляции рассчитывается как множественный: 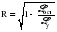 , (2.57) , (2.57)где: 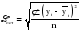 . .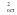 – остаточная дисперсия; – остаточная дисперсия;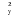 – общая дисперсия. – общая дисперсия.При построении многофакторных моделей по динамическим рядам возникает проблема мультиколлинеарности. Под мультиколлинеарностью в этом случае понимают наличие сильной корреляционной зависимости между факторными признаками. Мультиколлинеарность часто представляет опасность для правильного определения степени тесноты связи и оценки ее значимости. Мультиколлинеарность затрудняет проведение анализа, так как усложняется процесс выделения наиболее существенных факторов и искажается смысл коэффициента регрессии. Мультиколлинеарность возникает в том случае, когда факторными признаками выступают синтетические показатели. Например, в качестве факторов рентабельности могут рассматриваться объем реализации, производительность труда, фондоотдача, которые сильно коррелированы между собой. На практике считают два фактора сильно коррелированными, если парный коэффициент корреляции между ними по абсолютной величине больше 0,8. Довольно приблизительным методом обнаружения мультиколлинеарности является следующее правило. Фактор можно отнести к числу мультиколлинеарных, если коэффициент корреляции, характеризующий зависимость результативного признака от этого фактора больше, чем коэффициент множественной корреляции между результативным признаком и множеством остальных факторов. Меры по устранению мультиколлинеарности в основном сводятся к следующему:
Очистив таким образом уровни ряда динамики от автокорреляции и мультиколлинеарности, остается «подравнять» эти уровни по времени. Для этого необходимо рассмотреть вопрос о временном лаге. Временным лагом называется запаздывание (или опережение) процесса развития, представленного одним временным рядом, по сравнению с развитием, предоставленным другим рядом. Временной лаг определяется на основе перебора парных коэффициентов корреляции между абсолютными уровнями двух рядов динамики. Возможно наличие временного лага и в данных, которые изображают динамику годовых показателей. Следовательно, приведение данных к сопоставимому виду с точки зрения автокорреляции, коллинеарности и временного лага является предварительным условием построения многофакторной модели динамики. Построенная с соблюдением этих условий многофакторная регрессионная модель 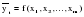 , (где знак показывает номер этапа) будет характеризовать среднее влияние факторных признаков на результативный признак за рассматриваемый интервал времени. Величина этого влияния, выраженная коэффициентами регрессии, частными коэффициентами эластичности и – коэффициентами будет изменяться от года к году. , (где знак показывает номер этапа) будет характеризовать среднее влияние факторных признаков на результативный признак за рассматриваемый интервал времени. Величина этого влияния, выраженная коэффициентами регрессии, частными коэффициентами эластичности и – коэффициентами будет изменяться от года к году.При продолжительном времени (свыше 10 лет) это будет означать недоучет влияния НТП, изменение энерговооруженности труда, замещение одного сырья другим и т.д. Эти недостатки отражения связи могут быть устранены несколькими способами. Один из них состоит в разбиении всего периода времени T на пять интервалов. При этом выдвигается гипотеза, что за равные интервалы времени коэффициенты регрессии изменяются несущественно. Исходя из этого, можно построить пять уравнений, аналогичных вышеприведенному. Следовательно, каждое значение коэффициента регрессии ai будет иметь пять оценок. Итак, получается временной ряд для каждого коэффициента регрессии. По этим рядам динамики можно построить временные модели (тренды) для каждого коэффициента по одному динамическому ряду. Так получается модель по уравнениям регрессии. Но при построении такой модели возникает ряд проблем. Прежде всего, при расчленении экономических динамических рядов и определяющих их факторов на интервалы, число интервалов должно быть достаточно велико, чтобы ряды динамики, составленные из этих интервалов, правильно отражали тенденцию изменения влияния факторных признаков на результативные. Число лет, входящих в один интервал, должно быть в 3–4 раза больше числа переменных, входящих в регрессионное уравнение. Однако исследователь часто располагает более короткими рядами динамики, следовательно, практически применять такие модели крайне затруднительно, а иногда и невозможно. Поэтому рассмотрим другие методы построения многофакторных моделей. Предположим, что зависимость результативного признака экономического явления от ряда факторных может быть записана уравнением: 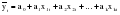 (2.58) (2.58)(t = 1, 2,..., k) и коэффициенты регрессии изменяются во времени по линейной функции так, что их можно записать уравнениями: 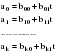 . (2.59) . (2.59)В этом случае уравнение регрессии примет вид: 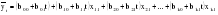 . (2.60) . (2.60)Параметры этого уравнения находятся по способу наименьших квадратов и показывают, как меняется во времени действие отдельных факторов на результативный признак рассматриваемого социально-экономического явления. Применение приведенного уравнения с большим числом факторов требует использования рядов с числом уровней в 6–7 раза больше числа параметров. Однако в данном случае рассматривались линейные тренды параметров уравнения регрессии, а при криволинейных трендах число параметров самого уровня значительно увеличивается и, следовательно, ряд динамики должен быть еще длиннее. Таким образом, пользоваться только что рассмотренным методом на практике бывает затруднительно. Особенно трудно вести оценку значимости параметров. Обычно имеющиеся в распоряжении исследования временные ряды за 20–25 лет недостаточны. Они должны быть значительно длиннее, чтобы были получены достаточно достоверные выводы. Контрольные вопросы к разделу II | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

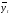 прямая
прямая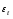
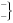
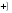
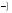
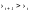 , то ставится «+»;
, то ставится «+»;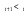 ставится «–».
ставится «–».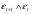
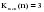 ;
;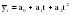 .
.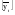 :
: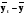 :
: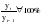
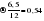 – поправка:
– поправка: 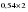 ;
; 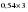 ...
...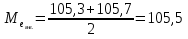
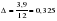 ;
;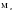 с учетом поправки:
с учетом поправки: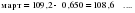
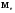 со средней
со средней 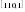 :
:
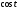
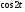
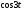
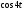
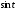
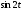
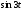
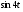
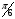
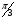
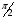
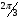
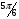
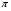
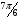
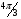
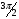
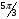
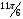
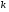
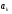
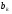
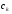
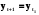 . Тогда
. Тогда