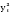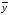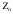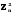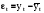Анализ временных рядов и прогнозирование. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
 Скачать 2.56 Mb. Скачать 2.56 Mb.
|
|
2.3. Моделирование тенденции Анализ и моделирование тенденции временного ряда целесообразно начинать с выявления наличия тенденции в целом. Для этой цели наиболее эффективны и дают хорошие результаты такие методы как кумулятивный Т-критерий. Кумулятивный Т-критерий позволяет определить наличие не только самой тенденции, но и ее математического выражения – тренда. Выдвигается основная гипотеза (Н0:) об отсутствии тенденции в исходном временном ряду. Расчетное значение критерия определяется по формуле: 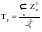 , (2.5) , (2.5)где: Zn – накопленный итог отклонений эмпирических значений уровней исходного ряда динамики от среднего его уровня; 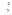 – общая сумма квадратов отклонений, определяемая по формуле: – общая сумма квадратов отклонений, определяемая по формуле: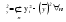 ; ;yt– исходные значения признака; 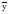 – средний уровень исходного ряда динамики; – средний уровень исходного ряда динамики;n – длина временного ряда (число уровней). Если анализируется достаточно длинный временной ряд, то для расчета значений критерия можно использовать нормированное отклонение: 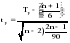 . (2.6) . (2.6)Расчетные значения кумулятивного Т-критерия и tp сравниваются с критическими при заданном уровне значимости . Если расчетное значение Tp превышает критическое (табличное) значение критерия (Ткр), то гипотеза об отсутствии тенденции отвергается, следовательно в исходном временном ряду существует тенденция, описываемая трендом. В противном случае, если Тр < Ткр или tp < tкр, признается отсутствие тенденции в ряду динамики. Пример. Имеются следующие данные об объеме вложений в ценные бумаги финансовой компании за период январь – октябрь 2009 г. Необходимо выявить тенденцию в изменении данного показателя. Промежуточные расчеты реализации кумулятивного Т-критерия представлены в таблице 2.2. Таблица 2.2 Промежуточные расчетные значения слагаемых кумулятивного Т-критерия
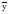 = = 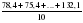 = = 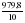 = 97,98; = 97,98; 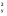 = 100 524,08 – (97,98)2 10 = 4 523,28. = 100 524,08 – (97,98)2 10 = 4 523,28.Соответственно, подставляя в формулу полученные значения, получаем: Тр = 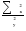 = = 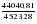  9,74 9,74Так как Тр (9,74) > Ткр (0,05; n=10; Tкр = 4,55), то гипотеза об отсутствии тенденции отвергается, следовательно во временном ряду объема вложений в ценные бумаги финансовой компании тенденция существует. Гипотезу о форме тренда также можно проверить с помощью кумулятивного T-критерия, где: Zn = (yt – 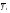 ) – накопленные суммы отклонений от тренда. ) – накопленные суммы отклонений от тренда.Фактическое значение Тр сравнивается с критическим для соответствующей функции f(t). Критические значения табулированы (приложение 5). Расчет статистической характеристики критерия Тр для проверки гипотезы о форме тренда рассмотрим на примере линейной функции (табл. 2.3). Для временного ряда валового надоя молока линейная функция равна: yt = 607,8 – 10,2t. Согласно проведенным расчетам фактическое значение Тр = 4,48. Оно больше критического T0.95(10) = 1,48, следовательно, линейная функция хорошо аппроксимирует тенденцию изменения валового надоя молока. Аналогично рассчитанное значение Тр = 0,98 для параболы II порядка yt = 594,93 – 10,2t + 0,39t2, что заметно ниже критического значения. Это дает основание с вероятностью 95% признать, что парабола не подходит для описания тенденции валового надоя молока. Таблица 2.3 Расчет кумулятивного критерия для проверки гипотезы о линейной форме тренда
Тенденция исходного временного ряда может быть трех видов: тенденция среднего уровня, дисперсии и автокорреляции. Тенденция среднего уровня может быть выражена с помощью графического метода. Аналитически тенденция выражается с помощью некоторой математической функции f(t), вокруг которой варьируют эмпирические значения исходного временного ряда изучаемого социально-экономического явления. При этом теоретические значения, то есть значения, полученные по трендовым моделям в отдельные моменты времени, являются математическими ожиданиями временного ряда. Тенденция дисперсии представляет собой тенденцию изменения отклонений эмпирических значений уровней временного ряда от теоретических, полученных по уравнению тренда. Тенденция автокорреляции выражает тенденцию изменения корреляционной связи между отдельными, последовательными уровнями временного ряда. Проверка на наличие тенденции среднего уровня и дисперсии может быть произведена методом сравнения средних уровней временного ряда и методом Фостера-Стюарта. Метод сравнения средних уровней временного ряда предполагает, что исходный временной ряд разбивается на две приблизительно равные части по числу членов ряда, каждая из которых рассматривается как самостоятельная, независимая выборочная совокупность, имеющая нормальное распределение. При этом решаются две задачи. I. Если временной ряд имеет тенденцию, то средние, вычисленные для каждой совокупности в отдельности, должны существенно, значимо различаться между собой. Если же расхождение незначимо, несущественно и носит случайный характер, то временной ряд не имеет тенденции средней. Таким образом, проверка гипотезы (Н0 : ) о наличии тенденции в исследуемом ряду сводится к проверке гипотезы о равенстве средних двух нормально распределенных совокупностей, то есть: Н0 : 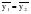 (2.7) (2.7)H1 : 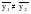 . .Гипотеза проверяется на основе t-критерия Стьюдента, расчетное значение которого определяется по формуле: 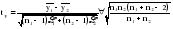 , (2.8) , (2.8)где: 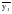 и и 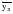 – средние уровни временного ряда согласно порядка разбиения; – средние уровни временного ряда согласно порядка разбиения;n1 и n2 – число уровней временного ряда, соответственно первой и второй части; 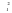 и и 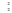 – дисперсия первой и второй части. – дисперсия первой и второй части.Расчетное значение (tp) критерия сравнивается с его критическим (табличным) значением (tкр) при уровне значимости и числе степеней свободы = n – 2. Если tp > tкр, то гипотеза о равенстве средних уровней двух нормально распределенных совокупностей отвергается, следовательно расхождение между вычисленными средними значимо, существенно и носит неслучайный характер, и, следовательно, во временном ряду существует тенденция средней и существует тренд. II. Если временной ряд имеет тенденцию, то дисперсии, вычисленные для каждой совокупности в отдельности, должны существенно и значимо различаться между собой. Если же расхождение между ними не значимо, то временной ряд не имеет тенденции дисперсии. Таким образом проверяется гипотеза (H0:) об отсутствии тенденции в дисперсиях в исходном временном ряду, которая сводится к проверке гипотезы о равенстве дисперсий двух нормально распределенных совокупностей, то есть: H0 : 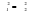 ; (2.9) ; (2.9)H1 : 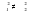 . .Гипотеза проверяется на основе F-критерия Фишера-Снедекора, расчетное значение которого определяется по формуле: 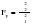 , если , если 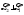 и 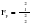 , если , если  . (2.10) . (2.10)Проверка гипотезы осуществляется на основе сравнения расчетного и критического значений F-критерия, полученного при заданном уровне значимости и числе степеней свободы 1 и 2. Если 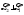 , то 1 = n2 – 1; , то 1 = n2 – 1;2 = n1 – 1. Если 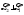 , то 1 = n1 – 1; , то 1 = n1 – 1;2 = n2 – 1. (2.11) Гипотеза о равенстве дисперсий двух нормально распределенных совокупностей отвергается, если Fp > Fкр. Следовательно, расхождение между вычисленными дисперсиями значимо, существенно, носит неслучайный характер и во временном ряду существует тенденция в дисперсиях и существует тренд. Следует заметить, что данный метод дает вполне приемлемые результаты лишь в случае рядов с монотонной тенденцией. Если же временной ряд меняет общее направление развития, то точка поворота тенденции может оказаться близкой к середине ряда, в силу этого средние двух отрезков ряда будут близки и проверка может не показать наличия тенденции. Пример. Имеются следующие данные о числе зарегистрированных разбоев в РФ (в тыс.): Таблица 2.4
Необходимо проверить наличие тенденции в данном ряду динамики методом сравнения средних уровней ряда динамики. Разобьем исходный ряд динамики на 2 равные части: в первую войдут значения показателя с 1999 по 2003 гг., во вторую – с 2004 по 2008 гг. Рассчитаем выборочные характеристики: 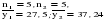 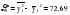 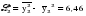 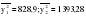 Если во временном ряду существует тенденция средней, то средние, вычисленные для двух совокупностей, должны значимо различаться между собой. Выдвигаем гипотезу 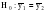 , проверяем ее на основе t-критерия , проверяем ее на основе t-критерияСтьюдента: 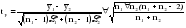 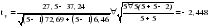 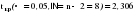 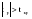 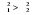 Следовательно гипотеза о равенстве средних двух совокупностей отвергается с вероятностью ошибки 5%, средние существенно различаются между собой, в ряду динамики числа зарегистрированных разбоев в РФ существует тенденция средней и, следовательно, во временном ряду существует тренд. Проверим гипотезу H0 о равенстве дисперсий двух нормально распределенных совокупностей на основе F-критерия Фишера-Снедекора: 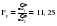 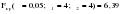 Так как 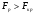 , то гипотеза H0 о равенстве дисперсий двух нормально распределенных совокупностей отвергается с вероятностью ошибки 5%, следовательно расхождение между дисперсиями существенно, во временном ряду числа зарегистрированных разбоев в РФ существует тенденция дисперсий, следовательно, во временном ряду существует тренд. , то гипотеза H0 о равенстве дисперсий двух нормально распределенных совокупностей отвергается с вероятностью ошибки 5%, следовательно расхождение между дисперсиями существенно, во временном ряду числа зарегистрированных разбоев в РФ существует тенденция дисперсий, следовательно, во временном ряду существует тренд. |