Анализ временных рядов и прогнозирование. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
 Скачать 2.56 Mb. Скачать 2.56 Mb.
|
Таблица 2.1Классификация временных рядов
Интервальные временные ряды представляются последовательностью значений уровней по показателю за определенный интервал времени (год, квартал, месяц и т.д.). Примером интервального ряда абсолютных величин является временной ряд, показывающий данные о выданных кредитах населению области 2009 г.:
Моментные ряды представляются в виде последовательности значений уровней по показателю, относящихся к конкретным моментам времени (на 1 января, на 1 июля и т. д.). Примером моментного ряда абсолютных величин может служить временной ряд, характеризующий данные об остатках задолженности предприятия по кредиту:
Из различного характера интервальных и моментных рядов вытекают некоторые особенности анализа уровней соответствующих рядов. Так, отдельные уровни моментного временного ряда абсолютных величин содержат элементы повторного счета, то есть в каждом последующем уровне содержится полностью или частично значение предыдущего уровня. Все это делает бессмысленным суммирование значений уровней моментного ряда. Значения же уровней абсолютных интервальных временных рядов, в отличие от уровней моментного ряда, не содержатся в предыдущих и последующих значениях уровней, их можно просуммировать, что позволяет получать ряды более укрупненных периодов, или ряды с нарастающими итогами, которые получаются путем последовательного суммирования смежных уровней. Эта особенность определяет способы расчета их средних уровней. Для интервальных рядов применяется средняя арифметическая простая и взвешенная. В моментных рядах с равностоящими уровнями – средняя хронологическая. Если интервалы времени в моментном ряду неравные, то предварительно вычисляется средняя за каждый период как полусумма уровней ряда на начало и конец периода. Из полученных результатов рассчитывается средняя взвешенная, где весами служит продолжительность каждого периода. По расстоянию между уровнями временные ряды подразделяются на ряды с равностоящими и не равностоящими уровнями во времени. Например, ранее приведенные данные об остатках задолженности предприятия по кредиту и данные о выданных кредитах населению области представляют собой временные ряды с равностоящими уровнями, то есть уровни представлены через равные, следующие друг за другом интервалы (моменты) времени. Если же во временных рядах прерывающиеся или неравномерные интервалы (моменты) времени, то такие ряды называются не равностоящими. Временные ряды подразделяются на стационарные и нестационарные. Случайные процессы, протекающие во времени приблизительно однородно и имеющие вид непрерывных случайных колебаний вокруг некоторого среднего значения, причем ни средняя амплитуда, ни характеристика этих колебаний не обнаруживают существенных изменений с течением времени в математической статистике называются стационарными. Всякий стационарный процесс можно рассматривать как процесс, неопределенно долго продолжающийся во времени. В связи с этим при проведении исследования в качестве начала отсчета можно выбрать любой момент времени. При этом на любом интервале времени должны быть получены одни и те же характеристики. В экономической практике в большинстве случаев приходится иметь дело со случайными процессами, имеющими вполне определенную тенденцию развития во времени. Такие процессы называются нестационарными, и временные ряды также называются нестационарными. Характеристики нестационарного случайного процесса меняются во времени, то есть зависят от начала отсчета. Особенностью экономического развития является тот факт, что случайные процессы в экономике как бы разбиваются на некоторую систематическую составляющую и случайные отклонения от нее. Применение методов теории случайных процессов для анализа экономических временных рядов в значительной мере связано с проблемой исследования случайной составляющей, ее сравнения с другими случайными величинами, обладающими известными свойствами, и вычисления статистических характеристик случайной компоненты. Это объясняется тем, что при краткосрочном и в определенной мере при среднесрочном прогнозировании результаты прогнозов тесно связаны со случайной составляющей, в то время как при долгосрочном прогнозировании основное значение имеет определение тенденции и взаимосвязи между факторами. Выбор вида временного ряда определяется целями анализа. Временные ряды могут быть изображены графически. Графическое изображение позволяет наглядно представить развитие явлений во времени и способствует проведению анализа уровней. Наиболее распространенным видом графического изображения для аналитических целей является линейная диаграмма, которая строится в прямоугольной системе координат. Наряду с линейной диаграммой для графического изображения временных рядов в целях популяризации широко используются столбиковые, секторные и другие виды диаграмм. Временные ряды охватывают отдельные обособленные периоды времени, в течение которых могут происходить изменения, вызывающие несопоставимость уровня ряда. Это делает временные ряды непригодными для анализа (несопоставимость уровней). К несопоставимости приводит изменение состава изучаемой совокупности, переход к другим единицам измерения, изменение методологии учета и расчета показателей, инфляционные процессы и т. п. Несопоставимыми временные ряды являются и в том случае, когда они составлены из неодинаковых по продолжительности периодов времени. Это относится, прежде всего, к рядам внутригодовой динамики с квартальными и месячными уровнями. При обнаружении несопоставимости уровней ряда должна применяться процедура смыкания рядов. Смыкание может быть произведено двумя способами. Первый способ заключается в том, что данные за предыдущие периоды умножаются на коэффициент перевода, равный отношению показателей на этот момент времени, когда произошло изменение условий формирования уровней ряда. Например, в современных условиях переоценка основных производственных фондов происходит ежегодно, и, следовательно, во временном ряду каждый год становится переходным, что постоянно требует расчета коэффициента перевода. Второй способ – уровень переходного периода принимается для 2-ой части ряда за 100%, и от этого уровня определяются соответствующие показатели (вперед или назад). При этом получается сопоставимый ряд относительных величин. Кроме того, анализ временных рядов должен также начинаться с выявления и устранения аномальных (нехарактерных) значений уровней ряда. Обычно аномальные значения можно обнаружить визуально, при помощи графического представления временных рядов, но, прежде чем «подправить» обнаруженные таким образом значения ряда, их необходимо подвергнуть дальнейшему количественному и качественному анализу. Нехарактерные уровни во временном ряду можно подразделить на три группы: – значения, отражающие объективное развитие процесса, но сильно отличающиеся от общей тенденции, так как они проявляют свои экстремальные воздействия крайне редко; – значения, возникающие вследствие изменений методики расчета; – значения, возникающие вследствие ошибок при измерении показателя, при записи и передаче информации, а также значения, связанные с различными катастрофическими явлениями, не влияющими на дальнейший ход развития явления, агрегировании и дезагрегировании показателей и т.д. Аномальные значения первой группы не всегда должны исключаться из временного ряда и могут даже оказаться полезными на этапе исследования причинно-следственного механизма развития явления. Наличие нехарактерных пиковых значений для одного и того же момента времени в различных временных рядах свидетельствует, как правило, о причинных связях между соответствующими показателями. Нехарактерные значения второй группы не должны исключаться из рассмотрения, а приниматься за «поворотные» (пороговые), начиная с которых должны быть пересчитаны по новой методике все предыдущие значения временного ряда. Аномальные значения третьей группы должны быть исключены из рассмотрения в любом случае, так как они искажают представление о характере развития явления и могут оказать существенное влияние на выводы, полученные в результате анализа ряда, содержащего такую искаженную информацию. Для выявления и замены аномальных значений третьей группы существует ряд аналитических методов, но большинство из них разрабатывалось для статистических совокупностей, содержащих независимые и случайные наблюдения, что не является справедливым для экономический временных рядов. Методика выявления аномальных наблюдений подробно приведена в п. 1.5. После приведения временных рядов к сопоставимому виду и выявления аномальных наблюдений, необходимо выявить закономерности динамики исследуемых явлений, так как это является главной целью при статистическом анализе социально-экономических явлений. Закономерности могут быть выявлены с помощью аналитических показателей, группировка которых представлена на рис. 2.1, то есть анализа абсолютной скорости и интенсивности развития социально-экономических явлений. Методология расчета этих показателей подробно дана в учебной литературе по общей теории статистики. В первую группу входят абсолютные показатели. Они характеризуют абсолютную скорость развития явления. Абсолютный прирост показывает величину абсолютных изменений уровня ряда в данном периоде по сравнению с предыдущем (цепной) или по сравнению с каким-то определенным периодом в прошлом (базисный). Абсолютное ускорение позволяет увидеть, насколько данная скорость (абсолютный прирост) больше или меньше предыдущей. Абсолютное значение одного процента прироста служит косвенной мерой базисного уровня и показывает, какая абсолютная величина скрывается за относительным показателем «один процент прироста». Вторую группу составляют относительные показатели, характеризующие интенсивность развития явлений. Если сравнение производится с постоянной базой (обычно это первый уровень ряда), то получают базисные темпы роста. Если сравнивается каждый последующий уровень с предыдущим, рассчитываются цепные темпы роста. Рис. 2.1. Аналитические показатели, характеризующие скорость и интенсивность изменения уровней временного ряда. Темп роста показывает, во сколько раз произошло изменение уровня ряда, поэтому он может быть равен нулю, если уровень ряда не изменился. Относительное ускорение есть темп прироста абсолютного прироста, а значит, он показывает на какую величину (в процентах) изменилась скорость изменения уровней ряда. Он вычисляется лишь в том случае, если абсолютный прирост, принятый за базу сравнения, является положительной величиной. Наконец третья группа включает обобщающие показатели, которые характеризуют среднюю величину скорости или интенсивности развития явления за продолжительный период (например, год или несколько лет и т.д.). Средний абсолютный прирост представляет собой обобщающий показатель абсолютной скорости изменения уровня ряда во времени. Этот показатель дает возможность установить, на сколько в среднем за единицу времени должен увеличиться (уменьшиться) уровень ряда, чтобы ряд от начального уровня за данное число периодов достиг конечного уровня. Сводной характеристикой интенсивности изменения уровней ряда служат средний темп роста и средний темп прироста. Средний темп роста показывает, во сколько раз в среднем за единицу времени изменился уровень временного ряда. Необходимость исчисления среднего темпа роста возникает вследствие колеблемости темпов роста от периода к периоду. Средний уровень ряда является обобщающей характеристикой его абсолютных уровней. Исчерпывающий анализ уровня ряда и его динамики требует параллельного использования всех перечисленных выше показателей. Анализ, основанный на использовании какого-либо одного из них, будет имеет односторонний характер и может привести к ошибочным выводам. Однако выявление закономерностей динамики социально-экономических явлений состоит не только в определении скорости и интенсивности развития, но имеет и другие цели:
2.2. Основные особенности статистического анализа одномерных временных рядов по компонентам ряда Задачей, решаемой при проведении любого статистического исследования, является определение объективных закономерностей развития социально-экономических явлений и процессов на основе анализа динамической информации. Статистические модели, построенные на основе временных рядов социально-экономических показателей, позволяют применять математико-статистические методы для описания закономерностей развития объектов экономики как в прошлом, так и в будущем. Используемые для целей и задач прогнозирования временные ряды экономических показателей обладают рядом особенностей. Временной ряд есть последовательность, в которой каждое значение содержит в себе прошлое для последующих состояний. Любая попытка предвидеть будущее без исследования временных рядов прошлого является малообоснованной, ненаучной и ошибочной. Поэтому для получения достаточно точных и надежных прогнозов, необходимо подробно изучить настоящее состояние явления или процесса. Всю процедуру статистического анализа одномерных временных рядов целесообразно разделить на пять стадий, которые представлены на рис. 2.2. Исследование скорости и интенсивности развития временных рядов часто не позволяет сразу определить основную тенденцию поступательного движения изучаемого явления. Это зависит от того, что уровни временного ряда со временем меняются, колеблются, но эта колеблемость не одинакова и может быть вызвана следующими причинами: влиянием общих факторов, определяющих главное направление, основную тенденцию развития явления; влиянием факторов общего характера, действующих периодически, сезонных колебаний и т.д.; влиянием специфических факторов, каждый из которых действует в разных направлениях, и их действие несущественно с точки зрения результатов развития явления, случайных колебаний. Рис. 2.2. Схема статистического анализа одномерных временных рядов Тип связи между компонентами временного ряда можно определить по нормальному распределению отклонений эмпирических значений уровней временного ряда от теоретических, полученных по уравнению тренда. В случае нормальности распределения абсолютных отклонений связь является аддитивной, а относительных – мультипликативной. Основные компоненты могут воздействовать на величину уровней временного ряда по-разному:
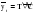 ; (2.1) ; (2.1)
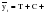 ; (2.2) ; (2.2)
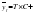 , (2.3) , (2.3)где: T – тенденция; С – сезонный компонент; – случайный компонент. Все компоненты временного ряда взаимосвязаны между собой и являются теоретическими понятиями. С этой точки зрения разделения временных рядов на компоненты – это теоретическая абстракция, так как данное разделение является чисто математической процедурой и осуществляется на базе статистических методов. Но, несмотря на условность такого расчленения фактических уровней рядов, такой прием может оказаться довольно полезным для решения разных проблем анализа и прогнозирования на базе временных рядов. По поводу расчленения временных рядов на компоненты известный русский ученый Четвериков Н.С. отмечал, что «расчленению подвергается динамика, а не само явление, участвующее не раздельно во всем сложном движении». Тип связи между компонентами можно также определить по динамике отклонений эмпирических значений уровней временного ряда от теоретических, полученных по уравнению тренда. Если абсолютные отклонения имеют тенденцию к росту, а относительные варьируют приблизительно на одинаковом уровне, то это свидетельствует о мультипликативной связи тренда и сезонного компонента. На практике выделить компоненты сложно, так как отдельные последующие значения временных рядов зависят от предыдущих. Поэтому неверно допускать, что факторы, влияющие на колебания уровней, независимы. Кроме того, статистическая совокупность, изучаемая в течение длительного периода, перестает быть такой же самой совокупностью, так как могут измениться основные факторы, влияющие на ее формирование. На первой стадии анализа для разложения рядов на составные компоненты и устранения влияния систематических компонент на изменение случайного компонента можно применить различные методы определения и установления отдельных неслучайных компонент временных рядов. В частности, при выявлении основной тенденции может быть использована схема анализа, представленная на рис. 2.3. Согласно данной схеме, прежде чем перейти к выделению основной тенденции развития явления, следует проверить гипотезу о том, существует ли она вообще. Отсутствие тенденции означает неизменность среднего уровня ряда во времени. Анализ основной тенденции во временных рядах выбор метода моделирования основной тенденции интерполяция экстраполяция метод скользящей средней тенденция автокорреляции Метод Лагранжа прогнозирование тенденции и развития метод конечных разностей метод наименьших квадратов метод плавного уровня проверка гипотезы о существовании тенденции тенденция средней тенденция дисперсии Рис. 2.3. Схема статистического анализа основной тенденции во временных рядах Экономическим явлениям свойственны элементы вероятностного характера. Наличие случайного в социально-экономических явлениях объясняется сложным переплетением параметров экономической системы, влиянием на них большого числа взаимосвязанных факторов, действующих в разных направлениях. Это ведет к вариации показателей уровней временного ряда. Ввиду концепции о наличии вероятностных элементов в динамике процессов, уровни временного ряда могут рассматриваться как сумма детерминированного и случайного компонентов. Детерминированный компонент выражается некоторой функцией и определяется уравнением основной тенденции или тренда. Проявление случайного компонента оценивается с некоторой вероятностью. Отклонения фактических уровней временного ряда от тренда рассматривается как стационарный случайный процесс. Выявление основной тенденции развития – это один из методов анализа и обобщения временных рядов. Он позволяет выразить особенности изменения явления во времени. Поэтому следует различать понятия:
Тренд – некоторая аналитическая функция, которая связывает единым «законом движения» все последовательные уровни временного ряда. Тренд описывает общую тенденцию на базе лишь одного фактора – фактора времени (t). Следовательно, не полностью описывает характер тенденции развития и не может рассматриваться как закон развития явления. Закон развития явления – выражает сущность, природу явления, не поддающуюся описанием тренда. При изучении временных рядов возникают следующие проблемы:
Использование особенностей временных рядов позволяет более точно строить по ним модель развития, отображающую процесс изменения явления во времени. При разложении рядов динамики на отдельные компоненты следует принимать во внимание, что компоненты исходного временного ряда, по существу не наблюдаемы и являются только теоретическими величинами, абстракциями. Но несмотря на это, такой подход к разбиению фактических уровней временных рядов может оказаться довольно полезным для решения проблем анализа и прогнозирования на базе временных рядов. Следует отметить, что уровни временного ряда не всегда являются составляющими всех трех компонентов одновременно. Единственным компонентом, который встречается во временных рядах является случайный компонент, который может быть представлен в сочетании с определенной тенденцией или с какими-то периодическими колебаниями. Чаще встречаются временные ряды, в которых можно установить тенденцию и случайный компонент, особенно при использовании годовых данных, где влияние сезонности не отражается. Аналитически данное положение можно выразить уравнением вида: 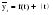 , (2.4) , (2.4)где: f(t) – некоторая функция времени, описывающая тенденцию исходного временного ряда, называемая трендом; (t) – случайная величина (случайный компонент). Функция f(t) определяет общую тенденцию развития изучаемого явления. Поэтому прежде чем приступать к моделированию и прогнозированию социально-экономических явлений и процессов необходимо проверить гипотезу о наличии тенденции в исходном временном ряду. |
