Анализ временных рядов и прогнозирование. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
 Скачать 2.56 Mb. Скачать 2.56 Mb.
|
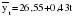 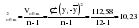 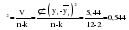 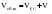 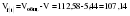 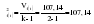 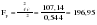 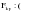 ; 1=k-1=1; 2=n-k=12-2=10); ; 1=k-1=1; 2=n-k=12-2=10); 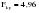 . .Следовательно, c вероятностью 95% можно утверждать, что уравнение линейного тренда подходит для описания тенденции исходного ряда объема платных услуг населению.
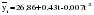 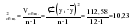 ; ; 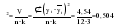 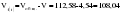 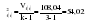 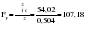 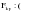 ; 1=k-1=2; 2=n-k=12-3=9); ; 1=k-1=2; 2=n-k=12-3=9); 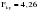 . .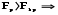 гипотеза отвергается. гипотеза отвергается.Следовательно, c вероятностью 95% можно утверждать, что уравнение параболы второго порядка подходит для описания тенденции исходного ряда динамики объема платных услуг населению одного из регионов РФ. Отдельно взятый критерий или метод при выборе формы тренда не обеспечивает правильность ее выбора. Необходим обязательно учет специфики объекта исследования, методов прогнозирования и оценки точности и надежности получаемых прогнозов. После того, как определена форма трендовой модели (уравнения), необходимо проанализировать наличие, характер и закон распределения отклонений эмпирических значений от теоретических, полученных по уравнению тренда. 2.5. Моделирование случайного компонента Исследование случайного компонента проводится с целью решения двух основных задач:
При правильном выборе формы тренда отклонения от него будут носить случайный характер, что означает, что изменение случайной величины t не связано с изменением t. Для этого определяются отклонения эмпирических значений от теоретических: t = yt – f(t) для каждого уровня исходного временного ряда. Проверяется гипотеза H0: о том, что значения случайной величины t случайны и величина t не зависит от времени. Методами проверки данной гипотезы являются следующие: коэффициент корреляции; критерий серий, основанный на медиане выборки; критерий «восходящих» и «нисходящих» cерий; критерий min и max. Наиболее простой способ сводится к расчету коэффициента корреляции между t (отклонениями от тренда) и фактором времени t, и проверке его значимости. Критерий серий, основанный на медиане выборки. Этапы реализации метода:
t > med – «+» t < med – «-» t = med – пропускается уровень или ставится «0». Таким образом получается ряд «+» и «-».
Выборка признается случайной, если одновременно выполняются неравенства ( = 0,05): 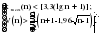 (2.37) (2.37)Если хотя бы одно неравенство нарушается, то гипотеза о случайности отклонений уровней временного ряда от тренда отвергается. Пример. Произведем оценку случайной компоненты в ряду динамики числа зарегистрированных разбоев (в тыс.) Таблица 2.14
Необходимо выявить случайную компоненту в данном ряду динамики с помощью критерия серий, основанного на медиане выборки. В качестве трендовой модели рассмотрим линейный тренд и параболу второго порядка.
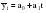 Рассчитаем параметры уравнения прямой, используя метод наименьших квадратов. Промежуточные вычисления отразим в таблице 2.15. 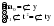 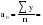 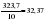 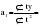  Таблица 2.15 Расчетная таблица для определения параметров линейного тренда, описывающего тенденцию изменения числа зарегистрированных разбоев в РФ за период 1999-2008 гг.
Таким образом, уравнение линейного тренда имеет вид: 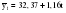 . .Рассчитаем отклонения 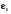 эмпирических значений числа зарегистрированных разбоев от выровненных по тренду (таблица 2.16, гр. 4). эмпирических значений числа зарегистрированных разбоев от выровненных по тренду (таблица 2.16, гр. 4).Проранжируем полученные отклонения в порядке убывания (таблица 2.16, гр. 5). Определим медиану отклонений 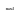 : :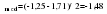 Cравним значения отклонений 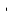 с с  : :
Получили ряд плюсов и минусов. Отразим результаты в таблице 2.16. Таблица 2.16 Расчетная таблица для определения параметров критерия серий, основанного на медиане выборки числа зарегистрированных разбоев в РФ за период 1999-2008 гг.
Выдвигается следующая гипотеза H0: если отклонения от тренда случайны, то и их чередование должно быть случайным. Для проверки выдвинутой гипотезы определим длину наибольшей серии: 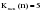 и число серий V(n)=3; n=10. Гипотеза не отвергается, если справедлива следующая система неравенств. 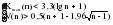 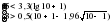 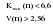 Оба неравенства выполняются, гипотеза о случайности отклонений уровней временного ряда от тренда в виде прямой 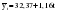 не отвергается. не отвергается.1. Произведем оценку случайности отклонений эмпирических значений числа зарегистрированных разбоев в РФ от теоретических, полученных по уравнению параболы второго порядка: 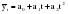 Для нахождения неизвестных параметров используем метод наименьших квадратов. Параметры данного уравнения определим из следующей системы: 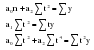 Промежуточные вычисления приведены в таблице 2.17. Таблица 2.17 Расчетная таблица для определения параметров параболы второго порядка, описывающей тенденцию изменения числа зарегистрированных разбоев в РФ за период 1999-2008 гг.
Подставив в данную систему вычисленные значения, получим следующие значения параметров уравнения параболы. 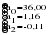 Полученное уравнение параболы второго порядка выглядит следующим образом: 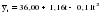 Рассчитаем отклонения 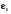 эмпирических значений признака от выровненных по тренду (таблица 2.18, гр. 4). эмпирических значений признака от выровненных по тренду (таблица 2.18, гр. 4).Проранжируем полученные отклонения в порядке убывания (графа 5). Определим медиану отклонений  : = : = 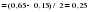 . .Сравним значения отклонений 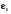 с с  : :
Получили ряд плюсов и минусов (графа 6). Отразим результаты в таблице. Таблица 2.18 Расчетная таблица для определения параметров критерия серий, основанного на медиане выборки
Выдвигается гипотеза H0: если отклонения от тренда случайны, то и их чередование должно быть случайным. Для проверки выдвинутой гипотезы определим:
Гипотеза не отвергается, если справедлива следующая система неравенств: 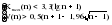 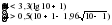 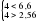 . .Оба неравенства выполняются, следовательно гипотеза о случайности отклонений уровней ряда динамики числа зарегистрированных разбоев от тренда в виде параболы 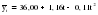 не отвергается. не отвергается.Пример. Произведем оценку случайности отклонений эмпирических значений объема платных услуг населению от теоретических, полученных на основе трендовых моделей, рассчитанных в таблице 2.10. Промежуточные расчеты приведены в таблице 2.19. |

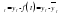 ).
).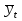
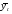
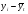
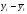
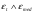
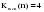 ;
;