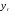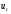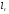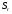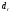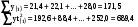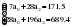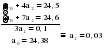Анализ временных рядов и прогнозирование. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
 Скачать 2.56 Mb. Скачать 2.56 Mb.
|
|
Метод Фостера-Стюарта основан на двух характеристиках S и d. 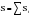 , ,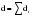 , ,где: 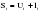 , ,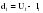 . (2.12) . (2.12)Суммирование производится по всем членам ряда. Значения Ut и lt определяются путем сравнения уровней исходного ряда динамики со всеми предыдущими. Если значение уровня ряда превышает по своей величине каждый из предыдущих уровней, то величине Ut присваивается значение 1, в остальных случаях она равна 0. Таким образом: 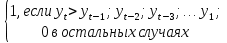 (2.13) (2.13)Наоборот, если значение уровня ряда меньше всех предыдущих, то lt присваивается значение 1. Таким образом: 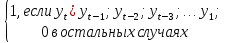 (2.14) (2.14)Показатели S и d асимптотически нормальные и имеют независимые распределения, но на них влияет порядок расположения уровней во времени. Показатель S применяется для обнаружения тенденции изменения в дисперсиях, d – для обнаружения тенденции в средней. После того, как для исследуемого ряда найдены фактические значения d и S, проверяется гипотеза о том, можно ли считать случайными разности (d – 0) и (S – ). Гипотезы проверяются на основе t-критерий Стьюдента, то есть: 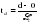 , (2.15) , (2.15)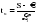 , (2.16) , (2.16)где: – математическое ожидание величины S, определенное для случайного расположения уровней во времени; 1 – средняя квадратическая ошибка величины S; 2 – средняя квадратическая ошибка величины d. Значения , 1, 2 табулированы. Если td > tкр (; = n – 1), то гипотеза об отсутствии тенденции в средней отвергается, следовательно в исходном временном ряду существует тренд. Если ts > tкр (; = n – 1), то гипотеза об отсутствии тенденции в дисперсиях отвергается, следовательно существует тенденция дисперсии и существует тренд. Пример. Проверим наличие тенденции во временном ряду числа зарегистрированных разбоев в РФ методом Фостера-Стюарта. Отразим в таблице 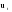 , ,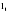 , ,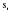 , ,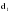 . .Таблица 2.5 Расчетная таблица для определения тенденции в ряду динамики числа зарегистрированных разбоев в РФ методом Фостера-Стюарта
Получили, что S=6, d=6 Выдвигаем две гипотезы:
Эти гипотезы проверяются с помощью t-критерия Стьюдента. По таблице значений средней 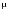 и стандартных ошибок и стандартных ошибок 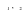 при n=10 находим при n=10 находим 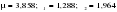 . .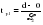 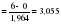 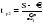 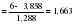 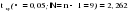 Так как 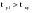 , то гипотеза об отсутствии тенденции в средней отвергается с вероятностью ошибки 5%, следовательно, средние существенно различаются между собой, во временном ряду числа зарегистрированных разбоев в РФ существует тенденция средней и, следовательно, во временном ряду существует тренд. , то гипотеза об отсутствии тенденции в средней отвергается с вероятностью ошибки 5%, следовательно, средние существенно различаются между собой, во временном ряду числа зарегистрированных разбоев в РФ существует тенденция средней и, следовательно, во временном ряду существует тренд.Так как 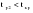 , то гипотеза об отсутствии тенденции в дисперсиях числа зарегистрированных разбоев в РФ не противоречит опытным данным, следовательно, дисперсии различаются незначительно, тенденция дисперсий во временном ряду отсутствует, тренда в данном ряду не существует. , то гипотеза об отсутствии тенденции в дисперсиях числа зарегистрированных разбоев в РФ не противоречит опытным данным, следовательно, дисперсии различаются незначительно, тенденция дисперсий во временном ряду отсутствует, тренда в данном ряду не существует.Фазочастотный критерий знаков разностей Валлиса и Мура. По данному критерию предполагается расчет разностей уровней временного ряда (yt+1 – yt). Нулевая гипотеза состоит в утверждении, что знаки этих разностей образуют случайную последовательность. Последовательность одинаковых знаков разностей называется фазой и рассчитывается число фаз h (без первой и последней фазы). Если знаки образуют случайную последовательность, то фактическое значение критерия запишется формулой (2.17). 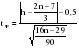 , (2.17) , (2.17)При больших выборах (n>30) поправка на непрерывность может быть опущена и формула расчета будет следующая: 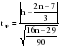 , (2.18) , (2.18)где: n – число уровней временного ряда, распределенных нормально; tф – фазочастотный критерий разностей; h – число фаз Если tф > 3, следовательно, данная последовательность случайна. Пример. Для иллюстрации данного метода рассмотрим данные строительной фирмы о производстве продукции по дням месяца (табл. 2.6). Таблица 2.6 Уровни и фазы временного ряда
В таблице 2.6 находим знаки отклонений (yt+1–yt) и проставляем нумерацию фаз. Получаем h=7, n=22. По таблице значений вероятности t (приложения 1) для фазочастотного критерия находим, что при вероятности 95%, то есть для 5%-ного уровня значимости t=1,96. Фактическое значение tф =2,55. Значит tф>t , то есть 2,55>1,96 нулевая гипотеза отвергается. Уровни ряда производства продукции строительной фирмы не образуют случайную последовательность, следовательно, имеют тенденцию развития. Критерий Кокса-Стюарта заключается в следующем, исходный временной ряд делится на три группы уровней. Численность первой и третьей групп должны быть равны между собой и составлять n/3 уровней каждая (при n, не делящемся на три, средняя треть уменьшается на одно и два значения). При этом осуществляется фиксация знаков отклонения каждого уровня третьей группы от соответствующего уровня первой группы. Из полученной суммы (S) положительных или отрицательных знаков (при возрастающем или убывающем тренде, соответственно) вычисляется ожидаемое значение n/6. Считается, что вычисленная разность распределена нормально со стандартным отклонением: 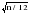 , то есть: , то есть: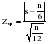 , (2.19) , (2.19)или при малых объемах (n<30) в формулу (2.19) вносится поправка Иейтса: 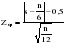 , (2.20) , (2.20)Для проверки расчетного значения Zф сравнивают его с табличным Z. При Zф >Z гипотеза о наличие (возрастающего или убывающего) тренда принимается. Пример. Воспользуемся данными предыдущего примера. Так как 22 не делится на 3, образуем обе трети, как если бы n было равно 24 (ni=24). Получаем уровни групп представленные в таблице 2.7. Таблица 2.7 Уровни групп
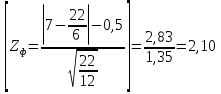 Мы получили семь отрицательных знаков из восьми. Проверка на убывающий тренд показала, что в зависимости от критерия (односторонний или двусторонний) критические значения равны: Z = 1,64 и Z = 1,96 для = 5%; Z = 2,33 и Z = 2,58 для = 1%. Значению Zф = 2,10 при двустороннем критерии соответствует вероятность Р 0,0357 (приложение 7). Убывающий тренд на 5%-ом уровне подтвержден. Таким образом, рассмотренные выше критерии основаны на определении знаков разностей последовательных уровней временных рядов или разностей определенных групп уровней ряда, то есть с их помощью предполагается определение наличия возрастающей или убывающей тенденции. Данные критерии дают удовлетворительные результаты, как правило, только для временных рядов не характеризующихся резкими колебаниями. При наличие ярко выражающихся колебаний в развитии социально-экономических явлений эти критерии могут давать противоречивые результаты. После того, как установлено наличие тенденции во временном ряду необходимо ее описать, то есть определить тип протекания процесса, имеющего место в данном явлении, направление роста и изменение, проходящие в нем. Можно выделить следующие типы процессов: I. По возрастанию или убыванию уровней ряда:
II. По наличию насыщения и стремлению к некоторой предельной величине:
III. По наличию экстремальных значений и перегибов:
Для выявления типа развития могут использоваться различные методы и критерии, в частности известные способы сглаживания: – сглаживание или механическое выравнивание отдельных уровней ряда динамики с использованием фактических значений соседних уровней; – выравнивание с применением кривой, приведенной между конкретными уровнями таким образом, чтобы она отображала тенденцию, присущую ряду, и одновременно освободила его от незначительных колебаний. Выбор метода выявления основной тенденции развития зависит от технических возможностей счета и от умения применять соответствующие методы, а также от задач, стоящих перед исследованием. Если надо дать общую картину развития, его грубую модель, основанную на механическом повторении одних и тех же действий по увеличению интервала времени, то можно ограничиться методом скользящей средней. Если же исследование требует подробного аналитического выражения движения во времени, то метод скользящей средней будет недостаточным. Надо использовать метод конечных разностей или метод наименьших квадратов. Все методы выявления основной тенденции развития определяются на основе изучения фактического развития динамики. Они не отрываются от наблюдаемого статистикой эмпирического материала. Методы выявления основной тенденции развития имеют разное логическое содержание и поэтому применяются ко временным рядам для разных целей. Основная их цель, как уже говорилось, заключается в том, чтобы вскрывать общие закономерности развития, затушеванные отдельными, иногда случайными обстоятельствами. Однако каждый из них имеет свои особенности. Метод скользящих средних используется в том случае, когда необходимо представить общую картину развития, основанную на механическом повторении одних и тех же действий по увеличению интервала времени. Метод скользящих средних дает оценку среднего уровня за некоторый период времени: чем больше интервал времени, к которому относится средняя, тем более плавным будет сглаживаемый уровень, но тем менее точно будет описана тенденция исходного ряда динамики. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней, начиная со второго, далее – начиная с третьего и т.д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя следующий. Отсюда название – скользящая средняя. Каждая скользящая средняя – это средний уровень за соответствующий период, который относится к середине выбранного периода. Определение скользящей средней по четному числу членов ряда осложняется тем, что средняя может быть отнесена только к середине между двумя датами, находящимися в середине интервала сглаживания. Если число членов скользящей средней обозначить через 2к, то срединным будет уровень, относящийся к «к+1/2» члену ряда, т.е. имеет место сдвиг периода, к которому относится уровень. Например, средняя, найденная для четырех членов, относится к середине между вторым и третьим периодами, следующая средняя – к середине между третьим и четвертым, и т.д. Для устранения этого используют процедуру центрирования, которая заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенной дате. Метод простой скользящей средней приемлем, если графическое изображение ряда динамики напоминает прямую линию. В этом случае не искажается динамика исследуемого явления. Покажем расчет 3-х и 4-членных скользящих средних на примере данных об объеме платных услуг населению одного из регионов РФ за период января-декабря 2009 г. (таблица 2.8). Таблица 2.8 Расчет 3-х и 4-членных скользящих средних объема платных услуг населению РФ
В случае, когда тенденция исходного ряда, характеризующего исследуемый процесс, не может быть описана линейным трендом, наиболее надежным является использование взвешенной скользящей средней. Взвешенная скользящая средняя отличается от простой скользящей средней тем, что уровни, входящие в интервал усреднения, суммируются с различными весами. Это связано с тем, что аппроксимация сглаживаемого ряда динамики в пределах интервала сглаживания осуществляется с использованием уровней, рассчитанных по полиному 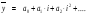 /i – порядковый номер уровня в интервале сглаживания/. Полином первого порядка – есть уравнение прямой, следовательно, метод простой скользящей средней является частным случаем метода взвешенной скользящей средней. Коэффициенты находятся методом наименьших квадратов. /i – порядковый номер уровня в интервале сглаживания/. Полином первого порядка – есть уравнение прямой, следовательно, метод простой скользящей средней является частным случаем метода взвешенной скользящей средней. Коэффициенты находятся методом наименьших квадратов.На первом этапе сглаживания определяются интервал сглаживания и порядок аппроксимирующего полинома. Принято считать, что при использовании полиномов высоких степеней и при меньших размерах интервалов сглаживание ряда динамики будет более гибким. Центральная ордината параболы, например, принимается за сглаженное значение соответствующего фактическим данным уровня. Поскольку отсчет времени в пределах интервала сглаживания производится от его середины, то сглаженное значение уровня равно параметру а подобранной параболы и является соответствующей скользящей средней. Поэтому для сглаживания нет необходимости прибегать к процедуре подбора системы парабол, так как величину а можно получить как взвешенную среднюю из «к» уровней. Например, если в интервал сглаживания входят пять последовательных уровней ряда со сдвигом во времени на один шаг, а выравнивание проводится по полиному второго порядка, то коэффициенты полинома находятся из условия: 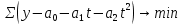 (2.21) (2.21)Учитывая, что для нечетных 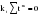 , получаем систему: , получаем систему: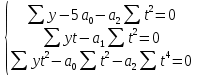 (2.22) (2.22)Для определения 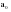 необходимо найти значения необходимо найти значения 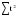 и и 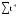 . .Так как интервал сглаживания равен к=5, то 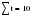 и и 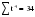 . .Нормальное уравнение, определяющее 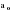 и и 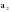 , в этом случае записывается следующим образом: , в этом случае записывается следующим образом: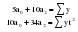 Решение этой системы относительно 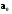 может быть представлено следующим образом: может быть представлено следующим образом: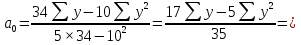 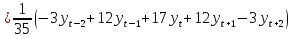 Аналогичным путем получают выражения и для других интервалов сглаживания по параболе второго и третьего порядка. 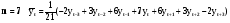 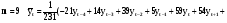 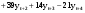 ) )Согласно приведенным формулам, веса симметричны относительно центрального уровня и их сумма с учетом общего множителя, вынесенного за скобки, равна единице. По данным рассмотренного выше примера об объеме платных услуг населению одного из регионов РФ за период январь – декабрь 2009 г. произведем расчет 7 – ми членных скользящих средних и проанализируем на их основе характер тенденции исходного временного ряда (таблица 2.9). В качестве аппроксимирующего полинома примем параболу второго порядка, параметры которой могут быть определены на основе решения следующей системы нормальных уравнений методом наименьших квадратов: 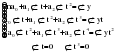 (2.23) (2.23)Отсчет времени в пределах интервала сглаживания произведем от его середины, то система уравнений упростится до следующего вида: 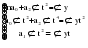 . (2.24) . (2.24)Промежуточные расчеты взвешенных скользящих средних более подробно могут быть представлены следующим образом: 2. 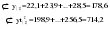 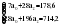 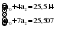 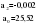 3. 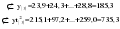 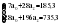 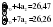 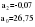 4. 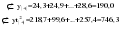 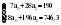 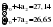 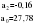  5. 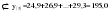 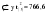 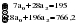 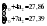 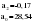 6. 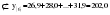 ; ;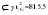 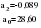 Анализ данных табл. 2.9 показал, что взвешенная скользящая средняя (гр. 18) на протяжении всего периода возрастает, т.е. за период с января по декабрь 2009 г. наблюдается рост объема платных услуг населения одного из регионов РФ. Таблица 2.9 Расчетная таблица для определения взвешенных скользящих средних объема платных услуг населению одного из регионов РФ за период январь-декабрь 2009 г. 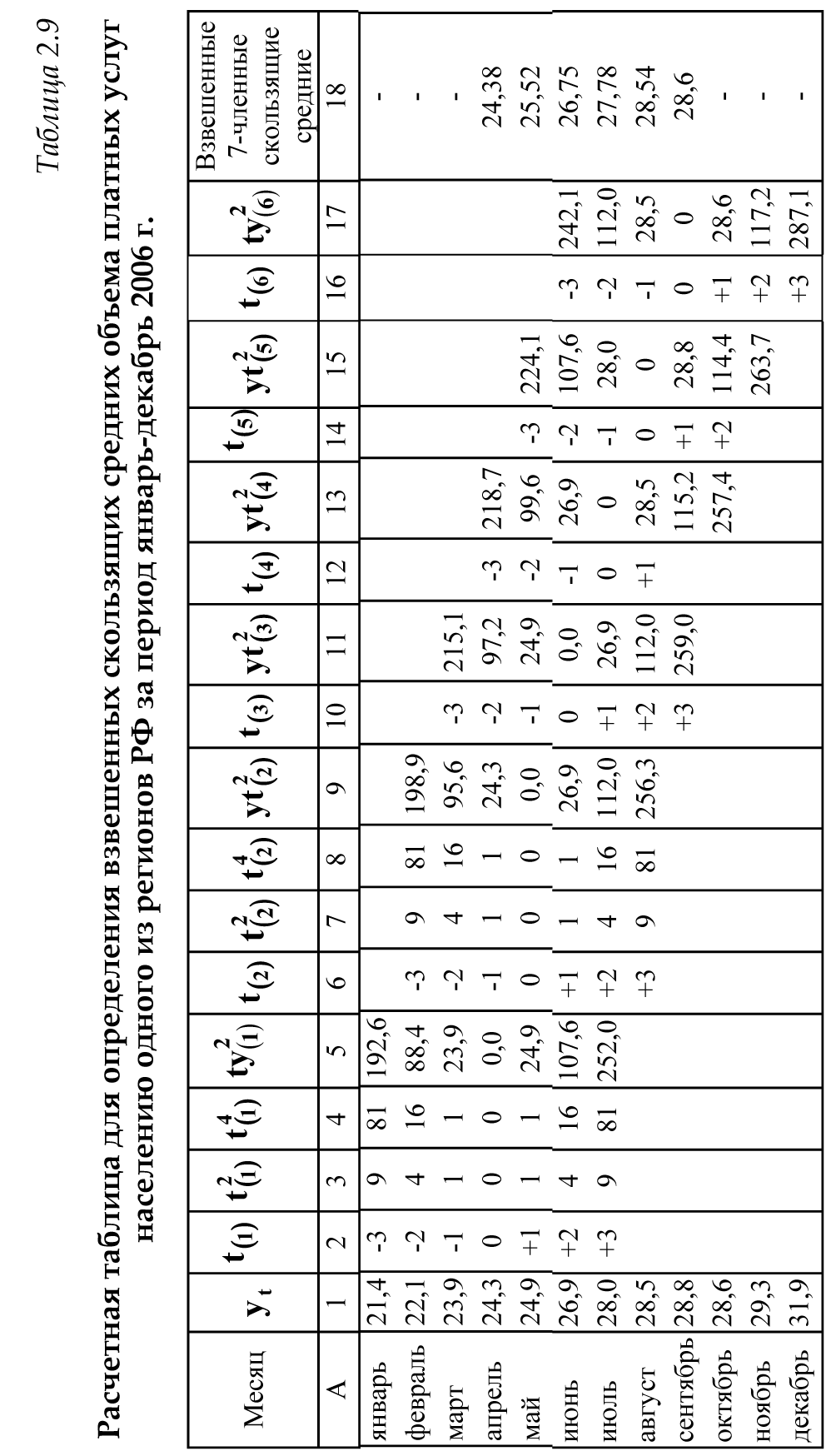 Метод плавного уровня по величине среднего абсолютного прироста придает изменению во времени характер изменения по прямой линии, а по величине среднего темпа роста – по показательной кривой. И тот и другой методы не покажут, как происходило развитие, так как их плавный уровень целиком зависит от начального и конечного уровней динамики. Метод Лагранжа является формальным методом, позволяющим установить математическую зависимость между уровнем временного ряда и временем, к которому он относится. Обобщением этой типизации и является моделирование (нахождение аналитической функции, выражающей развитие явления за рассматриваемый период времени). Метод аналитического выравнивания заключается в нахождении аналитической функции, выражающей развитие явления за рассматриваемый период времени. При этом решаются следующие задачи:
б) анализ схемы сбора фактических данных и определение параметров модели; в) определение методов преобразования исходных данных с целью сведения сложных уравнений к более простым; г) выявление степени близости теоретических и фактических данных. Найденная модель позволяет получить выровненные или, другими словами, теоретические значения уровней. Пример. Определим основную тенденцию ряда динамики объема платных услуг населению одного из регионов РФ за январь – декабрь 2009 г. Рассмотрим определение тенденции на основе полинома первой и второй степени, то есть прямой и параболы второго порядка, промежуточные расчеты параметров которых приведены в таблице 2.10. Таблица 2.10 Динамика объема платных услуг населению одного из регионов РФ за период январь-декабрь 2009 г. и определение параметров уравнения тренда методом наименьших квадратов 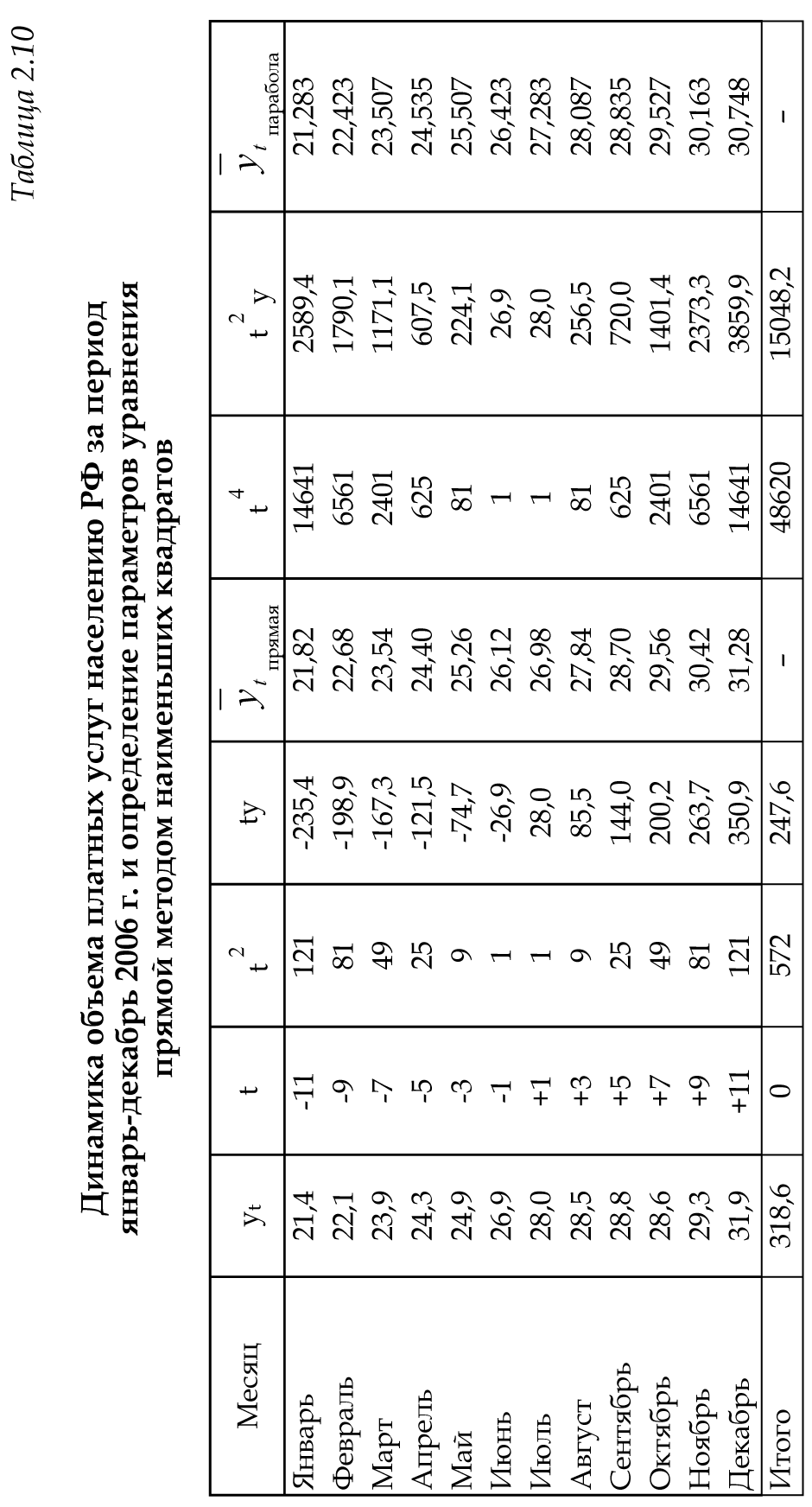 Для уравнения прямой параметры определяются путем решения следующей системы нормальных уравнений методом наименьших квадратов: 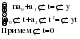 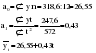 Для уравнения параболы второго порядка параметры могут быть определены на основе решения следующей системы нормальных уравнений методом наименьших квадратов: 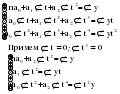 (2.25) (2.25)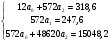 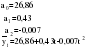 2.4. Выбор формы тренда Остановимся подробнее на проблеме выбора математической функции для описания основной тенденции развития, то есть выбора подобной реальной динамике формы уравнения. Для отображения основной тенденции развития явлений во времени или модели этого процесса применяются полиномы разной степени, экспоненты, логистические кривые и другие функции. Полиномы имеют следующий вид: полином первой степени 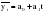 , ,полином второй степени 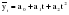 , (2.26) , (2.26)полином n-й степени 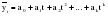 . .Наиболее простым путем решения проблемы выбора формы трендовой модели можно назвать графический, на базе общей конфигурации графика фактических уровней ряда. Однако при этом подходе риск ошибочного выбора кривой очень велик. Разные специалисты, исходя из одного и того же графика, могут прийти к разным заключениям по поводу формы уравнения. Правильность выбора уравнения в некоторой мере зависит от масштаба графика. Однако в несложных случаях подход графического выбора может дать вполне приемлемые результаты. Подбор класса выравнивающих кривых для временного ряда производится на основе качественного анализа представленного им процесса, а также если известны: 1, 2, 3…….i – первые, вторые, третьи и т.д. разности или абсолютные ускорения; Tp – темпы роста первых абсолютных приростов уровней; lgyi – первые абсолютные приросты логарифмов уровней; Тр – темпы роста. В этих случаях критерии выбора типа кривой следующие (табл. 2.11). Таблица 2.11 Критерии выбора класса выравнивающих кривых
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||