|
|
Анализ временных рядов и прогнозирование. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
1.5. Априорный анализ и его роль в статистическом
моделировании
Оценка эффективности и деловой активности субъектов экономического процесса и состояния социальной инфраструктуры общества во многом зависит от качества статистического анализа эмпирического материала, от того, насколько точно будут выявлены и научно обоснованны закономерности и тенденции развития.
Основные трудности, связанные с применением количественных математико-статистических методов, заключаются в том, что они достаточно нейтральны к исследуемым социально-экономическим процессам.
Поэтому основным этапом проведения статистического исследования на информационной базе, характеризующей реальные социально-экономические явления, является критическая оценка исходных данных с точки зрения их достоверности и научной обоснованности, которая в статистическом моделировании реализуется методами априорного анализа, включающего в себя:
выявление экономически обоснованных и существенных причинно-следственных связей между признаками и явлениями;
оценку однородности исследуемой совокупности;
анализ характера распределения совокупности по изучаемым признакам.
Понятия и категории, используемые при проведении анализа статистическими методами, должны быть точно определены.
Необходимо четко определить, к какому моменту или периоду времени относится исследуемое явление или процесс.
Одной из основополагающих предпосылок проведения научно-обоснованного статистического анализа, адекватно отражающего причинно-следственные связи и зависимости, тенденции развития реальных явлений и процессов в динамике, является однородность статистической совокупности.
Анализ однородности статистической совокупности целесообразно проводить в следующей последовательности:
определение степени однородности всей совокупности по одному или нескольким существенным признакам;
определение и анализ аномальных наблюдений;
выбор оптимального варианта выделения однородных совокупностей.
В статистической теории и практике разработаны различные подходы к оценке степени однородности.
Проблемой оценки однородности совокупности занимались такие известные ученые, как Ю. Аболенцев, Г. Кильдишев, В. Овсиенко и другие.
Наиболее сложным и дискуссионным является вопрос о способах и критериях выделения однородных групп объектов в пределах исходной совокупности.
Важной предпосылкой получения научно-обоснованных результатов статистического анализа и моделирования является проверка гипотезы о близости распределения эмпирических данных нормальному закону. Для нормального закона распределения характерно:
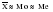 ; As = 0; Ex = 0 ; As = 0; Ex = 0
Одним из недостатков данного подхода к оценке характера распределения является наличие субъективности в анализе достаточности величины отклонения 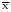 от Me и Mo от Me для подтверждения гипотезы. от Me и Mo от Me для подтверждения гипотезы.
Любая исследуемая совокупность, наряду со значениями признаков, сложившихся под влиянием факторов, непосредственно характерных для анализируемого объекта, может содержать и значения признаков, полученных под воздействием иных факторов, не характерных для изучаемого объекта.
Такие значения резко выделяются и, следовательно, использование методологии статистического анализа без изучения аномальных наблюдений приводит к серьезным ошибкам. Резко выделяющиеся из общей совокупности наблюдения требуют их изучения.
Причины появления в совокупности аномальных наблюдений можно условно подразделить следующим образом:
внешние, возникающие в результате технических ошибок;
внутренние, объективно существующие.
Аномальные наблюдения представляют интерес для исследователя, так как могут содержать, за счет влияния особых неучтенных факторов, особую информацию.
На практике, в зависимости от условий места и времени, влияние одних факторов в каждый конкретный исследуемый момент или промежуток времени значительнее, чем других.
Выбор того или иного метода выявления и анализа аномальных наблюдений определяется объемом совокупности, характером исследуемых процессов и задач (одномерные и многомерные).
При реализации одномерных задач как при анализе динамической, так и при анализе статической информации, наиболее широкое применение получил метод выявления аномальных наблюдений, основанный на определении q – статистики:
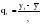 (1.1) (1.1)
где:
yt – отдельные уровни ряда;
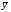 – средний уровень ряда; – средний уровень ряда;
σy– среднеквадратическое отклонение эмпирических значений уровней ряда от их среднего уровня.
Если для расчетного значения выполняется неравенство:
qt ≥ qкр (р) (1.2)
с заранее заданным уровнем вероятности, то данное наблюдение считается аномальным и, после логико-экономического анализа причин ошибок аномальности, подлежит замене скорректированным значением (в случае ошибки «I») и не подлежат корректировке (в случае ошибки «II»).
Корректировка осуществляется по схеме:
Рассчитывается новое значение уровня ряда:
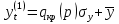 (1.3) (1.3)
2. 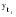 заменяется в ряду на заменяется в ряду на 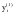 . .
Определяются новые характеристики ряда с 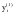 : : 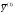 и и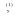 . .
Рассчитывается следующее значение:
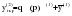 . (1.4) . (1.4)
Проверяется аномальность значения 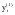 : :
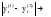 , (1.5) , (1.5)
где:
ε – заданный уровень точности определения 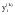 . .
Если данное условие выполняется, то значение 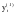 является скорректированным, не аномальным значением, занимает место является скорректированным, не аномальным значением, занимает место 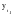 в ряду и анализу подвергается в ряду и анализу подвергается 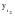 . .
Если условие не выполняется, то рекомендуется рассчитать 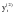 и проверить на аномальность. и проверить на аномальность.
Процесс корректировки носит итерационный характер.
В анализе временных рядов наибольшее распространение получил метод Ирвина, основанный на определении λ – статистики. При его использовании выявление аномальных наблюдений производится по формуле:
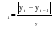 (1.6) (1.6)
Если расчетное значение превысит уровень критического (с заданным уровнем точности и числом наблюдений) (таблица 1.1), то расчетное значение признается аномальным.
Схема реализации данного метода аналогична предыдущей с той лишь разницей, что 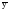 заменяется на yt-1(предыдущее значение уровня ряда). заменяется на yt-1(предыдущее значение уровня ряда).
Способ, основанный на расчете q – статистики применим для относительно стационарных рядов, так как при использовании для анализа динамических рядов, имеющих ярко выраженную тенденцию, он приведет к ошибкам.
Таблица 1.1
Табулированные значения λt
Число
наблюдений
|
λкр
|
0,95
|
0,99
|
2
3
10
20
30
50
100
|
2,8
2,2
1,5
1,3
1,3
1,1
1,0
|
3,7
2,9
2,0
1,8
1,7
1,6
1,5
|
Более корректным является использование статистики, в которой определяются отклонения от теоретических значений, полученных по уравнению тренда 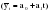 : :
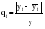 (1.7) (1.7)
В общем виде, схему градации статистических методов выявления аномальности в исходных данных можно представить следующим образом (рис. 1.1).
Основной задачей статистического исследования на этапе априорного анализа является выделение однородных групп (даже аномальных). В данном случае эффективно применять в анализе комбинационные группировки с развернутым сказуемым.
n≤20
n>20
Объем совокупности (n)
Обработка информации
Без использования ЭВМ
С использованием ЭВМ
Простейшие методы:
визуальный анализ;
графический метод.
математические методы;
статистические методы;
математико-статистические методы.
Рис. 1.1. Методы анализа аномальных наблюдений
Раздел II.
Моделирование динамики социально-экономических явлений и процессов
2.1. Временные ряды, их характеристики и задачи анализа.
Требования к исходной информации
Одна из важнейших задач статистики заключается в исследовании процесса изменения и развития изучаемых социально-экономических явлений во времени, решаемая с помощью построения временных рядов.
Временным рядом (динамическим рядом, английский термин «Time series») называется ряд расположенных в хронологической последовательности значений статистического показателя, характеризующего изменение социально-экономического явления во времени. В нем процесс экономического развития изображается в виде совокупности прерывов непрерывного, позволяющих детально проанализировать особенности развития при помощи характеристик, отображающих изменение параметров экономической системы во времени. Фактор времени здесь приобретает решающее значение.
Процесс изменения социально-экономических явлений во времени заключается в том, что происходит изменение воздействия на это развитие многих факторов социального, экономического, технологического и любого другого процесса, а фактор времени аккумулирует их влияние. Возьмем хотя бы экономические факторы. С течением времени они изменяются под влиянием внутренних причин экономического развития вообще, но с внешней стороны это развитие выглядит как развитие во времени. Всякий временной ряд включает два обязательных элемента: время (t) и конкретное значение показателя, или уровень ряда (yi).
Анализ временных рядов дает возможность проследить развитие явления, показать его основные тенденции. Выбор соответствующих приемов и способов анализа зависит от задач исследования и определяется характером исходных данных. Поэтому, приступая к анализу временных рядов, важно правильно их классифицировать (таблица 2.1).
|
|
|
 Скачать 2.56 Mb.
Скачать 2.56 Mb.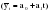 :
: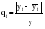 (1.7)
(1.7)
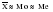 ; As = 0; Ex = 0
; As = 0; Ex = 0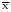 от Me и Mo от Me для подтверждения гипотезы.
от Me и Mo от Me для подтверждения гипотезы.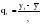 (1.1)
(1.1)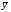 – средний уровень ряда;
– средний уровень ряда;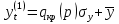 (1.3)
(1.3)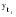 заменяется в ряду на
заменяется в ряду на 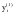 .
.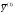 и
и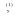 .
.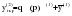 . (1.4)
. (1.4)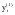 :
: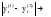 , (1.5)
, (1.5)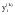 .
.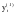 является скорректированным, не аномальным значением, занимает место
является скорректированным, не аномальным значением, занимает место 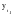 в ряду и анализу подвергается
в ряду и анализу подвергается 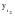 .
.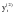 и проверить на аномальность.
и проверить на аномальность.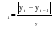 (1.6)
(1.6) заменяется на yt-1(предыдущее значение уровня ряда).
заменяется на yt-1(предыдущее значение уровня ряда).