Реферат по тех меху. Метод кинетостатики. Принцип Даламбера
 Скачать 44.38 Kb.
|
|
Министерство образования и науки РТ Государственное автономное профессиональное образовательное учреждение «Лениногорский нефтяной техникум» Реферат на тему: Метод кинетостатики. Принцип Даламбера. Выполнил студент группы АСУ-1-19 Мальковский М.В. Проверил преподаватель специальных дисциплин Галимова А.И. 2021 Содержание. Введение………………………………………………………………………………………...3 Метод кинетостатики…………………………………………………………………………..4 Сила инерции…………………………………………………………………………………...6 Определение принципа Даламбера……………………………………………………………8 Принцип Даламбера для материальной точки………………………………………………..9 Принцип Даламбера для механической системы……………………………………………10 Заключение…………………………………………………………………………………….11 Список используемой литературы…………………………………………………………...12 1. Введение. Метод кинетостатики – один из наиболее общих, эффективных и простых методов решения первой основной задачи динамики свободной и несвободной материальной точки и механической системы. В основе этого метода лежит принцип Германа–Эйлера–Даламбера. Метод кинетостатики. Запишем дифференциальное уравнение движения несвободной материальной точки в виде ma = F + R, где F и R - равнодействующие активных сил и реакций связей, действующих на несвободную материальную точку. Перенесем член ma в правую часть уравнения и введем в рассмотрение вектор  (1)равный произведению массы точки на величину ее ускорения, направленный противоположно вектору ускорения, и назовем введенный вектор даламберовой или просто силой инерции. Тогда основное уравнение динамики несвободной материальной точки примет вид  (2)Силы F, R, Ф образуют систему сходящихся сил, а полученное уравнение выражает условие равновесия данной системы сил, что и составляет принцип Даламбера для материальной точки: в каждый момент движения материальной точки активные силы, реакции связей и сила инерции образуют уравновешенную систему сил. Ускорение точки можно разложить на составляющие. Поэтому и сила инерции раскладывается на соответствующие составляющие, например, в естественной системе координат Ф = Фτ + Фn, где составляющие силы инерции определяются так: Фτ = -maτ; Фn = -man. Даламберову силу инерции, введенную по формуле (1), не следует смешивать с реальными физическими силами. Даламберова сила инерции не имеет источника своего возникновения - другого тела. Она вводится условно в ходе математических преобразований основного уравнения динамики, чтобы придать уравнениям динамики вид условия или уравнения равновесия. Следовательно, прикладывая силу инерции к движущейся материальной точке, мы можем говорить лишь об условном равновесии, приложенных к ней сил. Однако такое понимание динамического уравнения движения позволяет, используя уравнения равновесия статики, составлять динамические уравнения. Этот метод составления уравнений движения и называется методом кинетостатики. Например, спроектировав (2) на оси прямоугольной системы координат, можно получить три уравнения кинетостатики для материальной точки:  (3)которые представляют собой уравнения равновесия системы сходящихся сил, где к активным силам и реакциям связей, действующим на материальную точку, условно добавлена ее сила инерции. Так как принцип справедлив для любого мгновения времени, оси координат могут быть инерциальными или неинерциальными, неподвижными или подвижными. Важно лишь то, чтобы ускорение точки было определено в инерциальной системе координат или в абсолютном движении. Сила инерции. Система сил инерции твёрдого тела можно заменить одной силой, равной  и приложенной в центре О, и парой с моментом, равным  . Главный вектор системы сил, как известно, не зависит от центра приведения и может быть вычислен заранее. Т.к.  , то (2)Следовательно, главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению. Прикладывается главный вектор к точке приведения, которую можно назначить в любом месте, т.е. он не зависит от выбора этой точки. Если ускорение  разложить на касательное и нормальное, то вектор разложиться на составляющие  ,  С определением главного момента сил инерции возникает немало сложностей. Рассмотрим несколько частных случаев. 1. Поступательное движение. В этом случае тело никакого вращения вокруг центра масс С не имеет. Отсюда заключаем, что  , и равенство (1) даёт  .Следовательно, при поступательном движении силы инерции твёрдого тела приводят к одной равнодействующей, равной и проходящей через центр масс тела.2. Плоскопараллельное движение. Пусть тело имеет плоскость симметрии и движется параллельно ей. Вследствие симметрии главный вектор и результирующая пара сил инерции, так же как и центр масс С тела, лежат в плоскости симметрии. Тогда, помещая центр приведения в точке С, получим из равенства (1)  . С другой стороны 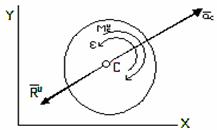 . Отсюда заключаем, что  Рис.1  (3)Таким образом, в рассмотренном случае движение системы сил инерции приводится к результирующей силе, равной [формула (2)] и приложенной в центре масс С тела (рис.1), и к лежащей в плоскости симметрии тела паре, момент которой определяется формулой (3). Знак минус в формуле показывает, что направление момента  противоположно направлению углового ускорения тела.3. Вращение вокруг оси, проходящей через центр масс тела. Пусть опять тело имеет плоскость симметрии, а ось вращения СZ перпендикулярна к этой плоскости и проходит через центр масс тела. Тогда данный случай будет частным случаем предыдущего. Но при этом  , а следовательно, и  .Таким образом, в рассмотренном случае система сил инерции приводится к данной паре, лежащей в плоскости, перпендикулярной к оси вращения тела, и имеющей момент  При решении задач по формулам (1) и (3) вычисляются модули соответствующих величин, а направление их указывают на чертеже. Определение принципа Даламбера. Принцип Даламбера звучит следующим образом: если к воздействующей на тело активной силе прикладывается дополнительная сила инерции, тело будет пребывать в равновесном состоянии. При этом суммарное значение всех действующих в системе сил, дополненное вектором инерции, получит нулевое значение. Согласно указанному принципу, в отношении каждой i-той точки системы, становится верным равенство: Fi+Ni+Ji=0, где: Fi -активно воздействующая на эту точку сила, Ni - реакция связи, наложенной на точку; Ji - сила инерции, определяемая формулой Ji=−miai (она направлена противоположно этому ускорению). Фактически, отдельно для каждой рассматриваемой материальной точки ma переносится справа налево (второй закон Ньютона): F=ma, F−ma=0. ma при этом называется силой инерции Даламбера. Такое понятие, как сила инерции, было введено еще Ньютоном. Согласно рассуждениям ученого, при условии движения точки под воздействием силы F=ma, тело (или система) – становится источником этой силы. При этом, согласно закону о равенстве действия и противодействия, ускоряемая точка будет влиять на ускоряющее ее тело с силой Ф Ф=−ma. Такой силе Ньютон дал название системы инерции точки. Силы F и Ф Ф будут равными и противоположными, но приложенными к разным телам, что исключает их сложение. Непосредственно на точку сила инерции воздействия не оказывает, поскольку для нее она представляет фиктивную силу. При этом точка оставалась бы в состоянии покоя, если бы, помимо силы F, на точку оказывала воздействие еще и сила. ЗАМЕЧАНИЕ 2: Принцип Даламбера позволяет применять при решении задач динамики более упрощенные методы статики, что объясняет его широкое применение в инженерной практике. На этом принципе основывается метод кинетостатики. Особенно он удобен в применении с целью установления реакций связей в ситуации, когда известен закон происходящего движения или он получен при решении соответствующих уравнений. Разновидностью принципа Даламбера выступает принцип Германа-Эйлера, фактически представлявшего собой форму данного принципа, но обнаруженную до появления публикации сочинения ученого в 1743 году. При этом принцип Эйлера не рассматривался его автором (в отличие от принципа Даламбера) в качестве основы для общего метода решения задач движения механических систем со связями. Принцип Даламбера считается более целесообразным в применении в случае необходимости определения неизвестных сил (для решения первой задачи динамики). Принцип Даламбера для материальной точки. Многообразие типов решаемых в механике задач нуждается в разработке эффективных методик составления уравнений движения для механических систем. Одним из подобных методов, позволяющих посредством уравнений описать движение произвольных систем, считается в теоретической механике принцип Даламбера. Опираясь на второй закон динамики, для несвободной материальной точки запишем формулу: ma¯=F¯+R¯, где R представляет реакцию связи. Принимая значение: Ф Ф¯=−ma¯, где Ф — сила инерции, получаем: F¯+R¯+Ф¯=0 Эта формула является выражением принципа Даламбера для материальной точки, согласно которому, для движущейся в любой момент времени точки геометрическая сумма воздействующих на нее активных сил и силы инерции получает нулевое значение. Этот принцип позволяет записывать уравнения статики для движущейся точки. Принцип Даламбера для механической системы. Для состоящей из n-точек механической системы, можно записать n-уравнений вида: Fi¯+Ri¯+Фi¯=0 При суммировании всех этих уравнений и введении следующих обозначений: ∑Fi=FE ∑Ri=R Фi=Ф, которые являются главными векторами внешних сил, реакции связей и сил инерции соответственно, получаем: ∑Fi+∑Ri+∑Фi=0, т. е. FE+R+Ф=0 Условием для равновесного состояния твердого тела является нулевое значение главных вектора и момента действующих сил. Учитывая это положение и теорему Вариньона о моменте равнодействующей в результате, запишем такое соотношение: ∑riFi+∑riRi+∑riФi=0 примем следующие обозначения: ∑riFi=MOF ∑riRi=MOR ∑riФi=MOФ главные моменты внешних сил, реакции связей и сил инерции соответственно. В итоге получаем: FE¯+R¯+Ф¯=0 M0F¯+M0R¯+M0Ф¯=0 Эти две формулы являются выражением принципа Даламбера для механической системы. В любой момент времени для движущейся механической системы геометрическая сумма главного вектора реакций связей, внешних сил, и сил инерции получает нулевое значение. Также нулевой будет и геометрическая сумма главных моментов от сил инерции, внешних сил и реакций связей. Полученные формулы являются дифференциальными уравнениями второго порядка из-за присутствия в каждом из них ускорения в силах инерции (второй производной закона движения точки). Принцип Даламбера позволяет решать методами статики задачи динамики. Для механической системы можно записывать уравнения движения в виде уравнений равновесия. Из таких уравнений можно определить неизвестные силы, в частности, реакции связей (первая задача динамики). Заключение. В заключении можно повторить определения из введения: Метод кинетостатики – один из наиболее общих, эффективных и простых методов решения первой основной задачи динамики свободной и несвободной материальной точки и механической системы. В основе этого метода лежит принцип Германа–Эйлера–Даламбера. А еще, можно сказать, все определения, приведенные в этом реферате, так или иначе связанны друг с другом. Список используемой литературы. Интернет-источники: 1.https://mydocx.ru/5-85668.html 2.https://docplayer.com/40146841-Metod-kinetostatiki-princip-germana-eylera-dalambera.html 3.https://spravochnick.ru/fizika/teoreticheskaya_mehanika/princip_dalambera_teoreticheskoy_mehaniki/#princip-dalambera-dlya-materialnoy-tochki |