Лекции Методы оптимальных решений. Методы оптимальных решений

• Название: Методы оптимальных решений
• Анкор: Лекции Методы оптимальных решений.doc
• Дата: 22.04.2017
• Размер: 466.5 Kb.
• Имя файла: Лекции Методы оптимальных решений.doc
• Тип: Решение; #5357
• страница: 5 из 9

5. МЕТОДЫ РЕШЕНИЯ

ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
5.1. Общая и основная задачи линейного программирования
К математическим задачам линейного программирования приводят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов (задача о раскрое, смесях и т.д.).

Во всех этих задачах требуется найти максимум или минимум линейной функции при условии, что ее переменные принимают неотрицательные значения и удовлетворяют некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные неравенства, так и линейные уравнения. Каждая из этиx задач является частным случаем общей задачи линейного программирования.
 Oбщей задачей линейного программирования называется задача, которая coстоит в определении максимального (минимального) значения функции:
(5.1)

при условии:

(5.2)
(5.3)
X_j  0 (j=1, 1; 1  n) (5.4)
где a_ij, b_i, с_j - заданные постоянные величины и k  m.
 Функция (5.1) называется целевой функцией (или линейной формой) задачи (5.1)-(5.4), а условия (5.2)-(5.4) - ограничениями данной задачи.
 Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (5.1) при выполнении условий (5.2) и (5.4), где k=m и 1=n.
 Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (5.1) при выполнении условий (5.3) и (5.4), где k=0 и 1=n.
 Совокупность чисел Х^ = (x₁, x₂, ..., x_n), удовлетворяющих ограничениям задачи (5.2)-(5.4), называется допустимым решением (или планом).
 План Х^ = (x₁, x₂, ..., x_n), при котором целевая функция задачи (5.1) принимает свое максимальное (минимальное) значение, называется оптимальным.

значение целевой функции (5.1) при плане X будем обозначать через F(X). Следовательно, Х^ - оптимальный план задачи, если для любого X выполняется неравенство F(X)  F(Х^) (соответственно F(X)  F(Х^)).
5.2. Геометрический метод решения

задач линейного программирования
Перепишем основную задачу линейного программирования в векторной форме: найти максимум функции
F=CX (5.5)
при условиях:

x₁P₁+x₂P₂+ ... +x_nP_n = P₀ (5.6)
Х 0 (5.7)
где C = (с₁, с₂, ..., с_n), Х = (х₁, х₂, ..., х_n); СХ - скалярное произведение; Р₁, Р₂, ..., Р_n и Р₀ - m-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных членах системы уравнений задачи.

 План X = (х₁, х₂, ..., х_n) называется опорным планом основной задачи линейного программирования, если система векторов P_j, входящих в разложение (5.6) с положительными коэффициентами x_j, линейно независима.
Непустое множество планов основной задачи линейного программирования образует выпуклый многогранник. Каждая вершина этого многогранника определяет опорный план. В одной из вершин многогранника решений (т.е. для одного из опорных планов) значение целевой функции является максимальным (при условии, что функция ограничена сверху на множестве планов). Если максимальное значение функция принимает более чем в одной вершине, то это же значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин.

Вершину многогранника решений, в которой целевая функция принимает максимальное значение, найти сравнительно просто, если задача, записанная в форме стандартной, содержит не более двух переменных или задача, записанная в форме основной, содержит не более двух свободных переменных. Haйдем решение задачи, состоящей в определении максимального значения функции:
F=c₁x₁ + с₂х₂ (5.8)
при условиях:

a_i1x₁+a_i2x₂  b_i (i=1, k) (5.9)
x_j  0 (i=1,2) (5.10)
Каждое из неравенств (5.9), (5.10) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми a_i1+a_i2=b_i (i=1, k), x₁=0 и x₂=0. В этом случае, если система неравенств (5.9), (5.10) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям.
 Так как множество точек пересечения данных полуплоскостей выпуклое, то областью допустимых решений (ОДР) задачи (5.8)-(5.10) является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.
Таким образом, исходная задача линейного программирования состоит в нахождении такой точки области допустимых решений, в которой целевая функция F принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин ОДР целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня c₁x₁+c₂x₂=h (где h - некоторая постоянная), проходящую через ОДР, и будем ее передвигать в направлении вектора C=(с₁; с₂) до тех пор, пока она не пройдет через последнюю ее общую точку с многоугольником ОДР. Координаты указанной точки и определяю оптимальный план данной задачи.

При нахождении решения задачи могут встретиться случаи, изображенные на рис. 5.1-5.4. Рис. 5.1 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке А. Из рис. 5.2 видно, что максимальное значение целевая функция принимает в любой точке отрезка АВ. На рис. 5.3 изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений, а на рис. 5.4 - случай, когда система ограничений задачи несовместна.

Oтметим, что нахождение минимального значения линейной функции при данной системе ограничений отличается от нахождения ее максимального значения при тex же ограничениях лишь тем, что линия уровня c₁x₁+c₂x₂=h передвигается не в направлении вектора С, а в противоположном направлении.










Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.
Тот факт, что оптимальное решение находится в одной из вершин многоугольника ОДР, позволяет сделать еще два важных вывода:
если оптимальным решением являются координаты вершины многоугольника ОДР, значит, сколько вершин имеет ОДР, столько существует целевых функций и столько оптимальных решений по этим функциям может иметь задача.
 поскольку, чем больше ограничений имеет задача, тем больше вершин, тo, следовательно, чем больше целевых функций и, следовательно, тем больше оптимальных решений по этим функциям.
Из рисунков можно сделать вывод, что вершина, координаты которой являются оптимальным решением, определяются углом наклона прямой, описывающей целевую функцию. Значит, каждая вершина будет соответствовать оптимальному решению для некоторой целевой функции. Итак, нахождение решения задачи линейного программирования (5.8)-(5.10) на основе ее геометрической интерпретации включает следующие этапы.
этапы нахождения решения задачи линейного программирования:
 Строят прямые, уравнения которых получаются в результате замены в ограничениях (5.9) и (5.10) знаков неравенств на знаки точных равенств.

 Находят полуплоскости, определяемые каждым из ограничений задачи.

 Находят многоугольник решений (ОДР).

 Строят вектор C=(с₁; с₂).

 Строят прямую c₁x₁+c₂x₂=h, проходящую через многоугольник решений.

 Передвигают прямую c₁x₁+c₂x₂=h в направлении вектора С, в результате чего-либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве планов.

 Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.
5.3. Графическое решение задачи распределения ресурсов
Пусть для двух видов продукции П₁и П₂ требуются трудовые, материальные и финансовые ресурсы. Наличие ресурсов каждого вида и их нормы расхода, необходимые для выпуска единицы продукции, приведены в табл. 5.1.
Таблица 5.1

Характеристика	Вид продукции		располаг.
	П1	П2	ресурс
Резервы:
трудовые	1	4	14
материальные	3	4	18
финансовые	6	2	27
выпуск	1	1	---
прибыль	4	8,5	---
план	х1	х2	---

составим математическую модель задачи.
x₁+4x₂  14

x₁+4x₂  18

(5.11) x₁+2x₂  27

x₁  0, x₂ 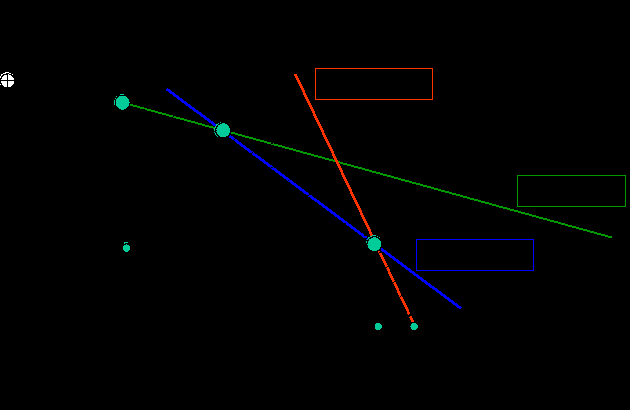


математическая модель представляет собой систему линейных неравенств. Значит ОДР нашей задачи выпуклый многоугольник. Для удобства построения неравенства можно записать в форме, аналогичной уравнениям в отрезках:
x₁/14+x₂/7/2  1

x₁/6+x₂/9/2  1

(5.12) x₁/9/2+x₂/27/2 1

x₁  0, x₂ 
Если мы хотим найти оптимальное решение, то должны принять целевую функцию. Допустим, мы хотим, чтобы решение было оптимальным в смысле максимизации суммарного выпуска. Тогда целевая функция:
F=x₁+x₂  max (5.13)
Эту зависимость представим в виде x₂= F-x₁. Из графика данного уравнения (Рис. 5.1) следует, что tg= 1, при этом  =135^о, а величина F равна отрезку, отсекаемому прямой функции цели на оси координат. Если прямую перемещать параллельно самой себе в направлении, указанном стрелками, то эта величина будет возрастать. Очевидно, что оптимальным решением будут координаты точки С (x^₁; x^₂). При этом F=F^.

На основании рассмотренного, можно сделать исключительно важный вывод: оптимальным решением являются координаты вершин ОДР. А из этого вывода следует метод решения задачи линейного программирования.
метод решения задачи линейного программирования:
 Найти вершины ОДР, как точки пересечения ограничений.

 Определить последовательно значения целевой функции в вершинах.

 Вершина, в которой целевая функция приобретает оптимальное значение, является оптимальной вершиной.

 Координаты оптимальной вершины являются оптимальными значениями искомых переменных.
Если направление целевой функции совпадает с направлением одной из сторон, то у задачи будет, по крайней мере, два решения. В таком случае говорят, что задача имеет альтернативные решения. А это значит, что одно и то же оптимальное значение целевой функции может быть получено при различных значениях переменных.
Тот факт, что оптимальное решение находится на вершине ОДР, дает еще два очень важных вывода:
 если оптимальным решением являются координаты вершин ОДР, значит, сколько вершин имеет ОДР, столько оптимальных решений может иметь задача.

 поскольку чем больше ограничений, тем больше вершин, то, следовательно, чем больше ограничений, тем больше оптимальных решений.
Как видно на Рис. 5.1, вершина, координаты которой являются оптимальным решением, определяется углом наклона прямой, описывающей целевую функцию. Значит, каждая вершина будет соответствовать оптимальному решению для некоторой целевой функции. Поясним это на рассмотренном ранее примере. Раньше мы находили оптимальное решение по максимизации суммарного выпуска F₁=x₁+x₂max. Найдем оптимальные решения еще для четырех целевых функций:
F₂=x₂max (максимизация выпуска продукции П₂)

F₃=x₁max (максимизация выпуска продукции П₁)

F₄=4x₁+8,5x₂max (максимизация прибыли)

F₅=(1+3+6)x₁ + (4+4+2)x₂ = 10х₁+10х₂ max (минимизация используемых ресурсов).
Для каждой целевой функции, так же как и для F₁, можно построить линию целевой функции и определить вершину, в которой целевая функция будет иметь оптимальное значение. Результаты решения задачи по пяти целевым функциям сведем в таблицу 5.2, из анализа которой можно сделать вывод: координаты каждой вершины могут быть оптимальным решением в некотором смысле.