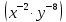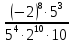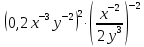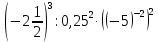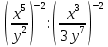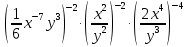Методические указания по математике для специальностей СПО. Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине
 Скачать 471.38 Kb. Скачать 471.38 Kb.
|
Методические рекомендации по выполнению практических работРаздел 1. Алгебра. Тема 1.1. Развитие понятия о числе. Практическая работа №1. Выполнение действий над натуральными, целыми, рациональными и действительными числами. Цель: повторить правила действий над числами. Натуральные числа - это числа, которые используются при счете: 1, 2, 3... и т.д. Ноль не является натуральным. Натуральные числа принято обозначать символом N. Два числа отличающиеся друг от друга только знаком, называются противоположными, например, +1 и -1, +5 и -5. Знак "+" обычно не пишут, но предполагают, что перед числом стоит "+". Такие числа называются положительными. Числа, перед которыми стоит знак "-", называются отрицательными. Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z. Рациональные числа - это конечные дроби и бесконечные периодические дроби . Например, Множество иррациональных чисел обозначается J. Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел. Действительные числа обозначаются символом R. Задания к практической работе. Вариант 1 Вычислить: а)3 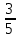 ∙ ∙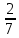 + 1 + 1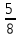 ∙ ∙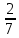 ; б) ( ; б) (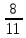 - -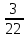 ) ∙ 44 ; в) ( 2 ) ∙ 44 ; в) ( 2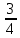 + 4 + 4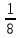 ) ∙ 1 ) ∙ 1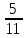 ; г) 6 ; г) 6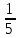 ∙ 4. ∙ 4.Упростить выражение и найти его значение при а = 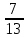 а) 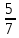 а + а + 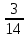 а . а .Докажите, что значение выражения 4,8 + 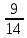 х - 0,5х - х - 0,5х - 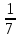 х не зависит от значения х. х не зависит от значения х. Найдите значение выражения: 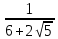 + + 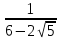 Расположите в порядке возрастания числа: 1,5; 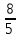 ; ; 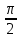 ; ; 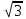 ; ; 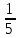 . .Вариант 2 1. Вычислить: а) 9 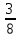 ∙ 2 ∙ 2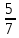 - 2 - 2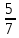 ∙ 7 ∙ 7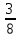 ; б) ( ; б) (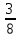 + + 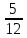 ) ∙ 24 ; в) 1 ) ∙ 24 ; в) 1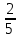 ∙ (1 ∙ (1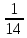 - - 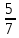 ) ; г)8 ) ; г)8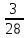 ∙ 5. ∙ 5.2. Упростить выражение и найти его значение при а = 4 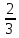 а) 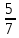 а + а + 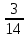 а . а .3 .Докажите, что значение выражения 4,8 + 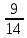 х - 0,5х - х - 0,5х - 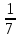 х не зависит от значения х. х не зависит от значения х. 4. Найдите значение выражения: 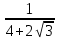 + + 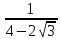 5.Расположите в порядке возрастания числа: 3,1; 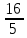 ; ; 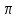 ; ; 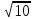 ; ; 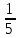 . .Критерии оценки: «5» - ставится за 5 верно решенных заданий; «4» - ставится за 4 верно решенных задания; «3» - ставится за 3 верно решенных задания; «2» - если решено менее 3 заданий. Литература. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. Тема 1.1. Развитие понятия о числе. Практическая работа №2 Решение задач на выполнение действий с приближенными числами Цель: закрепить полученные знания по теме в процессе решения задач. Абсолютной погрешностью приближения называется модуль разности между истинным значением величины и её приближённым значением. , где — истинное значение, — приближённое. Относительной погрешностью приближения называется отношение абсолютной погрешности к модулю приближённого значения величины. , где — истинное значение, — приближённое. Относительную погрешность обычно вызывают в процентах. Пример. При округлении числа до единиц получается число . Относительная погрешность равна Важнейшей задачей приближённых вычислений помимо нахождения приближённого значения величины является оценка абсолютной или относительной погрешности. Например, число 3, 14 является приближённым значением числа , при этом абсолютная погрешность не превосходит . Задания к практической части. 1. Записать числа в виде двойного неравенства.
2. Округлить с точностью до 0,01 следующие числа.
3. Найти границу относительной погрешности числа а.
Критерии оценки:
Литература: Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. Тема 1.2. Корни, степени и логарифмы Практическая работа №3 Вычисление и сравнение корней. Цель: закрепить полученные знания по теме в процессе решения задач. Вычисление и сравнение корней. Свойства корней степени n: если a 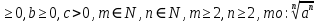 = a ; = a ; 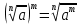 ; ; 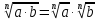 ; ; 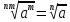 ; ; 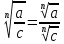 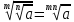 Пример: 1) Вычислите: 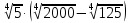 = = 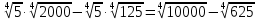 = = 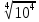 - - 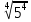 = 10 - 5 = 5 = 10 - 5 = 5Задания к практической части.
Критерии оценки: «5» - ставится за 5 верно решенных заданий; «4» - ставится за 4 верно решенных задания; «3» - ставится за 3 верно решенных задания; «2» - если решено менее 3 заданий. Литература. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. Тема 1.2. Корни, степени и логарифмы Практическая работа №4 Решение задач на свойства степени Цель: способствовать закреплению навыков работы со степенями с рациональными показателями. Свойства степени с рациональным показателем. 1. 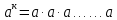 ( к раз) ( к раз) 2. 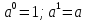 3. 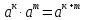 4. 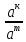 = = 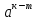 5. 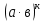 = =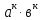 6. 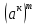 = =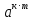 7. 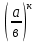 = = 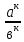 Примеры. 1. 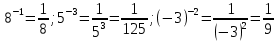 2. 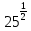 = = 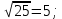 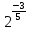 = = 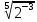 = = 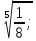 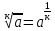 3. 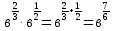 ; ;4. 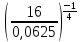 = = 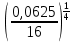 = = 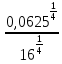 = = 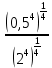 = = 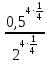 = = 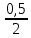 = 0.25 = 0.255. 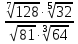 = = 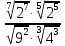 = = 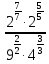 = = 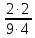 = = 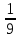 Задания к практической работе.
Критерии оценки: «5» - ставится за 5 верно решенных заданий; «4» - ставится за 4 верно решенных задания; «3» - ставится за 3 верно решенных задания; «2» - если решено менее 3 заданий. Литература. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

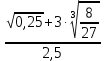
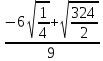
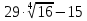
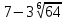
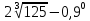
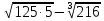
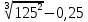
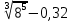
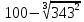
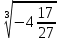
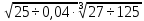
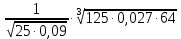
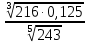
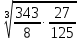
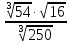
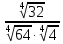
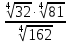
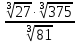
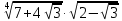
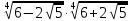
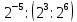
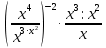
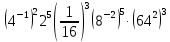
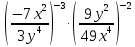
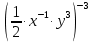 :
: