Методические указания по математике для специальностей СПО. Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине
 Скачать 471.38 Kb. Скачать 471.38 Kb.
|
ТЕМА5.2. Многогранники.Практическая работа № 23Построение сечений многогранников. Цель: закрепление знаний, отработка навыков построения сечений. Пояснения к работе: При построении сечений следует руководствоваться следующими правилами: 1) 2 точки, лежащие в одной плоскости, можно соединять прямой линией; 2) Стороны сечения, лежащие в параллельных плоскостях – параллельны. Задания к практической работе. (Постройте самостоятельно)
Критерии оценки: «5» ставится за 4 верно решенных заданий; «4» ставится за 3 верно решенных задания; «3» ставится за 2 верно решенных задания; «2» - если решено менее 2 заданий. Литература. Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил. ТЕМА 5.2. Многогранники.Практическая работа № 24Объем параллелепипеда. Объем призмы. Цель: закрепление знаний, отработка навыков решения задач, используя свойства призмы и пирамиды. Пояснения к работе. 1. Изучите п. 194, 195,196, 197, 199, 200 (с. 339 – 347 ). Геометрия 7-11 Погорелов 2. Ответьте на вопросы: а) Сформулируйте свойства объемов многогранников. б) Запишите в тетрадях формулы объемов прямой и наклонной призм. 3. Найдите объем и площадь полной поверхности куба, длина диагонали грани которого равна 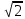 см. см.4. Запишите формулу объема пирамиды. 5. Объем пирамиды ABC равен V. Найдите объем призмы, в основании которой лежит треугольник АВС, а высота равна высоте пирамиды. 6. Боковые ребра треугольной пирамиды попарно перпендикулярны, а длины их равны а, в, с. Найдите объем пирамиды. 7. Как изменится объем куба, если длину его ребра увеличить в два раза? Задания к практической работе:
Критерии оценки: «5» - ставится за три верно решенные задачи; «4» - ставится за две верно решенные задачи; «3» - ставится за одну верно решенную задачу; «2» - менее одной задачи. Литература. Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил. Тема 5.3. Тела и поверхности вращения Практическая работа № 25 Объемы и поверхности тел вращения. Цель: контроль и закрепление знаний, умений, навыков студентов по теме объёмы и поверхности тел вращения. Задания к практической работе.
Критерии оценки: «5» ставится за 3 верно решенных задания; «4» ставится за 2 верно решенных задания; «3» ставится за 1 верно решенное задание; «2» – если решено менее 1 задания. Литература. Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил. Раздел 6. Начала математического анализа. Тема 6.1. Последовательности. Практическая работа № 26 Предел функции. Цель: способствовать закреплению навыков вычисления пределов. Функцию y=f(x) называют непрерывной в точке x=a, если выполняется тождество: Функцию y = f(x) называют непрерывной в точке x = a, если предел функции при x 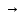 а равен значению функции в точке x = a. а равен значению функции в точке x = a. Функция непрерывна на отрезке [a, b], если она непрерывна в каждой точке отрезка. Пример 1. Вычислить: 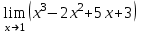 . .Решение. Выражение х3 – 2х2 + 5х + 3 определено в любой точке х, в частности, в точке х = 1. Следовательно, функция у = х3 – 2х2 + 5х + 3 непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1. Имеем: 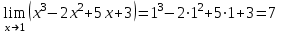 . .Ответ: 7. Для решения следующего примера нам потребуются правила вычисления предела функции в точке. Правило 1. 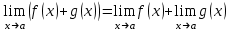 . .Правило 2. 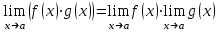 . .Правило 3. 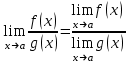 . .Пример 2. Вычислить 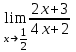 . .Выражение 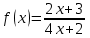 определено в любой точке х определено в любой точке х 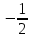 , в частности, в точке х = , в частности, в точке х = 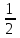 . Следовательно, функция у = f (x) непрерывна в точке х = . Следовательно, функция у = f (x) непрерывна в точке х = 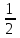 , значит предел функции при стремлении х к , значит предел функции при стремлении х к 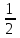 равен значению функции в точке х = равен значению функции в точке х = 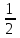 . Имеем: . Имеем: 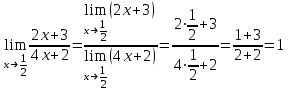 . .Ответ: 1. Задания к практической работе.
Критерии оценки: «5» - ставится за 5 верно выполненных заданий; «4» - ставится за 4 верно сделанных задания; «3» - ставится за 3 верно выполненных задания; «2» - если решено менее 3 заданий. Тема 6.2. Производная и её применение. Практическая работа № 27 Производная. Понятие о производной функции, ее геометрический и физический смысл. Цель: закрепление знаний, отработка навыков вычисления производных. Пояснения к работе. Определение. Производной функции у = f 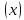 в точке х называется предел отношения приращения функции в точке х называется предел отношения приращения функции 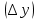 в этой точке к приращению аргумента в этой точке к приращению аргумента 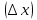 , когда , когда 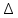 х стремится к 0. Обозначение: f х стремится к 0. Обозначение: f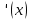 = =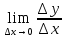 Производная функции у = f(х), в точке х0, выражает скорость изменения функции в этой точке. 2. Если функция задана законом прямолинейного движения S = S(t), то S' (t) –? Скорость движения в момент времени t - это производная по перемещению S' (t) = v(t) Что есть вторая производная от закона движения? Скорость изменения скорости этого движения, т.е. ускорение а(t) = v' (t) = S' ' (t). С физической точки зрения дифференцирование – определение скорости изменения переменной величины. Производная, таким образом, играет роль скорости изменения зависимой переменной y по отношению к изменению независимой переменной х. Выясняем формулы из физики, где используется производная. υ(t) = х'(t) – скорость. a(t) = υ'(t) – ускорение. I(t) = q'(t) – сила тока. с(t) = Q'(t) – теплоемкость. d(l) = m'(l) – линейная плотность. K(t) = l'(t) – коэффициент линейного расширения. ω(t) = φ'(t) – угловая скорость. e(t) = ω'(t) – угловое ускорение. Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности. N(t) = A'(t) – мощность. F(x)= A'(x) – Сила есть производная работы по перемещению. Е = Ф'(t) – ЭДС индукции F = р'(t) – 2 закон Ньютона.
Таблица производных
Задания к практической работе. Найдите производную функции.
Найти необходимые величины.
Критерии оценки: «5» ставится за 8-10 верно решенных заданий; «4» ставится за 7-6 верно решенных задания; «3» ставится за 5 верно решенных задания; «2» - если решено менее 5 заданий. Тема 6.2. Производная и её применение. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Провести сечение через сторону нижнего основания и противоположную ей вершину верхнего основания. Определить площадь сечения.
Провести сечение через сторону нижнего основания и противоположную ей вершину верхнего основания. Определить площадь сечения. Определить площадь диагонального сечения.
Определить площадь диагонального сечения. . Найдите объем и площадь полной поверхности параллелепипеда.
. Найдите объем и площадь полной поверхности параллелепипеда. Найдите объем параллелепипеда и площади его диагональных сечений, если площадь его боковой поверхности равна 220
Найдите объем параллелепипеда и площади его диагональных сечений, если площадь его боковой поверхности равна 220 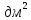 .
.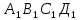 , в котором В
, в котором В 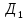 перпендикулярно
перпендикулярно 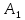 С. Найдите его объем, если В
С. Найдите его объем, если В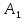 С = 8см АВ = 3 см
С = 8см АВ = 3 см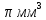 .
.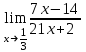
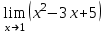
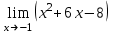
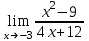
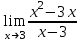
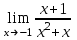
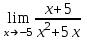
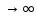
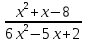
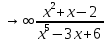
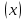
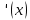
 f
f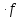
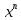
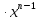
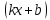
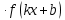
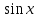
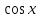
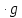
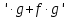
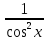
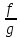
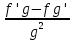
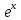
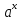
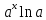
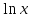
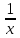
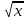
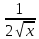
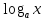
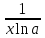
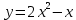 3.1
3.1 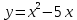 3.6
3.6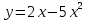 3.11
3.11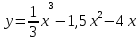 3.2
3.2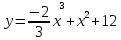 3.7
3.7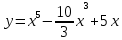 3.12
3.12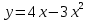 3.3
3.3 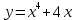 3.8
3.8 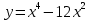 3.13
3.13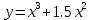 3.4
3.4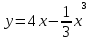 3.9
3.9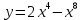 3.14
3.14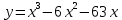 3.5
3.5 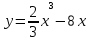 3.10
3.10 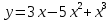 3.15
3.15