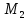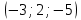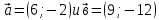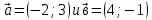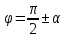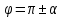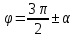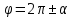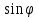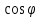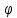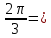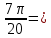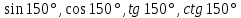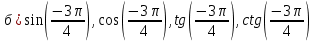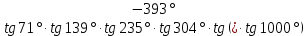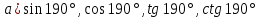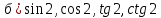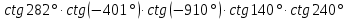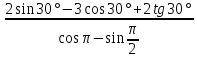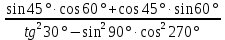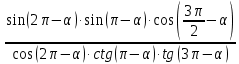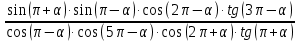Методические указания по математике для специальностей СПО. Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине
 Скачать 471.38 Kb. Скачать 471.38 Kb.
|
|
Тема 1.2. Корни, степени и логарифмы Практическая работа №5 Степени с рациональным показателем. Цель: способствовать закреплению навыков решения выражений содержащих степени с рациональным показателем. Свойства степени с рациональным показателем. 1. 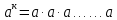 ( к раз) 2. ( к раз) 2. 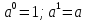 3. 3. 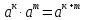 4. 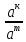 = = 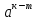 5. 5. 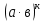 = =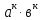 6. 6. 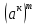 = =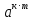 7. 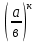 = = 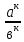 Примеры. 1. 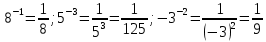 2. 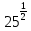 = = 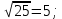 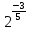 = = 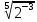 = = 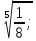 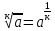 3. 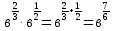 ; ;4. 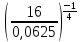 = = 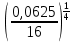 = = 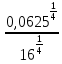 = = 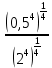 = = 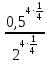 = = 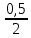 = 0.25 = 0.255. 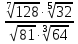 = = 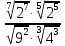 = = 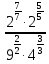 = = 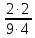 = = 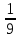 Задания к практической работе.
Критерии оценки: «5» - ставится за 9-10 верно решенных заданий; «4» - ставится за 7-8 верно решенных задания; «3» - ставится за 5-6 верно решенных задания; «2» - если решено менее 5 заданий. Литература. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. Тема 1.2. Корни, степени и логарифмы Практическая работа №6 Решение показательных уравнений и неравенств Цель: способствовать закреплению навыков решения показательных уравнений и неравенств. Определение: показательными называются уравнения и неравенства, содержащие переменную в показателе степени. Примеры. 1) 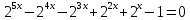 (разложение на множители) (разложение на множители)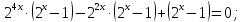 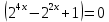 или или 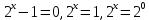 , х = 0 , х = 0 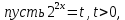 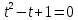 ; D = - 3 ; D = - 3 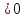 , корней нет. , корней нет. Ответ: 0 2) 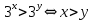 , т.к. основание а = 3 , т.к. основание а = 3 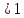 3) ( 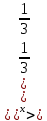 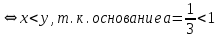 ; ;4) 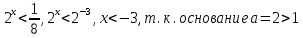 Задания к практической работе.
Критерии оценки: «5» - ставится за 9-10 верно решенных заданий; «4» - ставится за 7-8 верно решенных задания; «3» - ставится за 5-6 верно решенных задания; «2» - если решено менее 5 заданий. Литература. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. Тема 1.2. Корни, степени и логарифмы Практическая работа №7 Нахождение значений логарифмов. Цель: способствовать закреплению навыков вычисления логарифмов. Определение: Логарифмом положительного числа b по основанию a называется показатель степени, в которую надо возвести a, чтобы получить b. 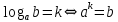 . .Свойства логарифмов. 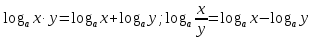 ; ; 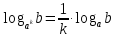 ; ; 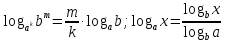 (a (a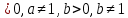 ). Основное логарифмическое тождество: ). Основное логарифмическое тождество: 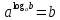 Примеры. 1) Упростите выражение: 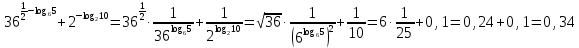 ; ;2) Найдите значение выражения: 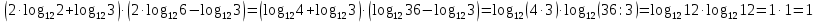 ; ;3) На сколько сумма чисел 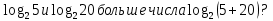 Решение: 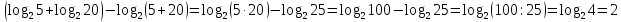 . . Задания к практической работе.
Критерии оценки: Оценка «5» ставится за 9-10 верно выполненных заданий; «4» - ставится за 7-8 верно выполненных заданий; «3» - за 5-6 верно выполненных задания; «2» - менее выполненных 5 заданий. Литература. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. Тема 1.2. Корни, степени и логарифмы Практическая работа № 8 Решение задач на свойства логарифмов. Цель: способствовать закреплению навыков вычисления логарифмов. Задания к практической части.
Критерии оценки: «5» - ставится за 9-10 верно выполненных заданий; «4» - ставится за 7-8 верно выполненных задания; «3» - за 5-6 верно выполненных задания; «2» - за менее 5 заданий. Литература. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. Тема 1.2. Корни, степени и логарифмы Практическая работа № 9 Решение логарифмических уравнений и неравенств. Цель: закрепление знаний, отработка навыков решения логарифмических уравнений и неравенств. Пояснения к работе: Определение: Логарифмом положительного числа b по основанию a () называется показатель степени, в которую надо возвести a, чтобы получить b. 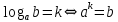 . .Свойства логарифмов. 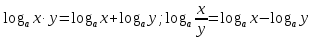 ; ; 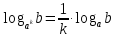 ; ; 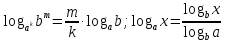 (a (a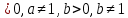 ). Основное логарифмическое тождество: ). Основное логарифмическое тождество: 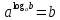 Примеры. 1) Решите уравнение: 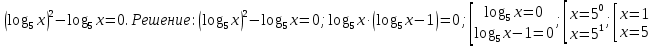 ответ: 1;5 ответ: 1;52) Решите неравенство: 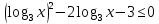 Решение: Обозначив Решение: Обозначив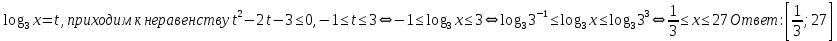 Задания к практической работе.
Критерии оценки: «5» - ставится за 9-10 верно выполненных заданий; «4» - ставится за 7-8 верно выполненных заданий; «3» - за 5-6 верно выполненных заданий; «2» - менее пяти заданий. Литература. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. Раздел 2. ГЕОМЕТРИЯ Тема 2.1. Прямые и плоскости в пространстве. Практическая работа № 10 Параллельность прямых и плоскостей Цель: закрепление знаний, отработка навыков применения параллельности прямых и плоскостей при решении задач. Пояснения к работе: Определение 1. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек Определение 2. Прямая и плоскость в пространстве называются параллельными, если они  . .Определение 3. Две плоскости называются параллельными, если они  . .Пример: Концы данного отрезка длиной 125 см отстоят от плоскости на 100 см и 56 см. Найти длину его проекции.
Задания к практической работе.
Критерии оценки: «5» ставится за 8 верно решенных заданий; «4» ставится за 6-7 верно решенных заданий; «3» ставится за 4-5 верно решенных задания; «2» - если решено менее 4 заданий. Литература. Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил. Тема 2.1. Прямые и плоскости в пространстве Практическая работа № 11 Перпендикулярность прямых и плоскостей Цель работы: закрепление знаний, отработка навыков применения перпендикулярности прямых и плоскостей при решении задач. Пояснения к работе: Определение 1. Две прямые в пространстве называются перпендикулярными 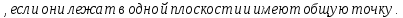 Определение 2. Прямая в пространстве называется перпендикулярной плоскости Определение 2. Прямая в пространстве называется перпендикулярной плоскости 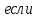 она перпендикулярна любой прямой она перпендикулярна любой прямой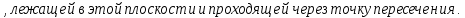 Определение 3. Две плоскости называются перпендикулярными, если третья плоскость, проведенная Определение 3. Две плоскости называются перпендикулярными, если третья плоскость, проведенная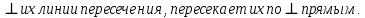 Пример: Из данной точки проведены к данной плоскости две наклонные, равные каждая 2 см; угол между ними равен 60 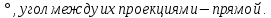 Найти расстояние данной точки от плоскости. Решение. Треугольник, в который входят обе наклонные - равносторонний, все углы равны по 60 Найти расстояние данной точки от плоскости. Решение. Треугольник, в который входят обе наклонные - равносторонний, все углы равны по 60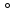 , все стороны равны по 2 см. Но если равны наклонные, то равны и их проекции. Тогда из треугольника, лежащего в плоскости, по теореме Пифагора находим его катеты: , все стороны равны по 2 см. Но если равны наклонные, то равны и их проекции. Тогда из треугольника, лежащего в плоскости, по теореме Пифагора находим его катеты: 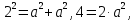 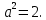 Из треугольника ( перпендикуляр – наклонная – проекция) находим перпендикуляр: Из треугольника ( перпендикуляр – наклонная – проекция) находим перпендикуляр: 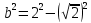 , , 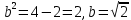 . .Задания к практической работе.
Критерии оценки: «5» ставится за 6 верно решенных заданий; «4» ставится за 5 верно решенных задания; «3» ставится за 3-4 верно решенных задания; «2» - если решено менее 3 заданий. Литература. Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил. Тема 2.2 Координаты и векторы. Практическая работа № 12 Тема: Действия над векторами. Цель: закрепление знаний, отработка навыков выполнения действий над векторами. Пояснения к работе: Основные формулы: 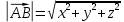 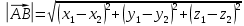 ; ; 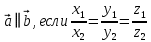 ; ; 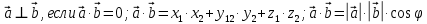 ; ; 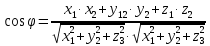 ; ; 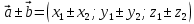 ; m ; m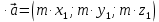 ; ;Пример: 1) Дано: 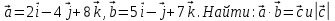 Решение: 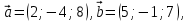 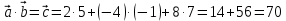 . .2) Коллинеарны ли векторы 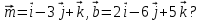 Ответ: Нет, т. к. Ответ: Нет, т. к. 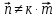 3) Найти угол между векторами 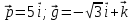 . Решение: . Решение: 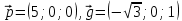 , , 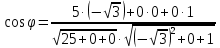 = = 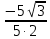 = - = - 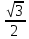 Задания к практической работе:
Критерии оценки: «5» ставится за 5 верно решенных заданий; «4» ставится за 4 верно решенных задания; «3» ставится за 3 верно решенных задания; «2» - если решено менее 3 заданий. Литература. Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил. Раздел 3 ОСНОВЫ ТРИГОНОМЕТРИИ Тема 3.1. Основные тригонометрические тождества Практическая работа № 13 Использование формул приведения для преобразования тригонометрических выражений. Цель работы: закрепление знаний, отработка навыков работы с формулами приведения. Таблица формул приведения.
Пример 1. Найдите значение 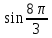 Решение. 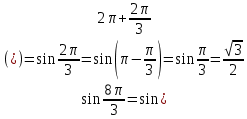 Пример 2. 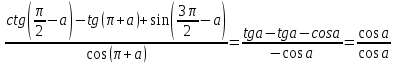 =1 =1Задания к практической работе.
Критерии оценки: «5» ставится за 4 верно решенных заданий; «4» ставится за 3 верно решенных задания; «3» ставится за 2 верно решенных задания; «2» - если решено менее 2 заданий. Литература. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

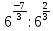
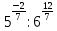
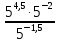
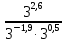
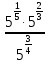
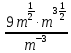
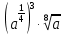
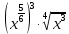
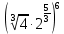
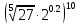
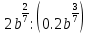
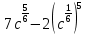
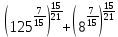
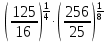
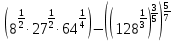
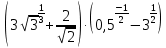
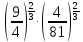
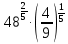
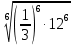
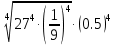
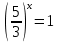
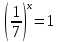
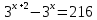
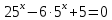
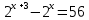
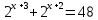
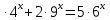
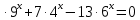
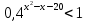
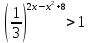
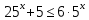
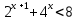
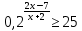
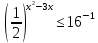
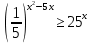
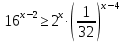
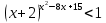
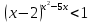
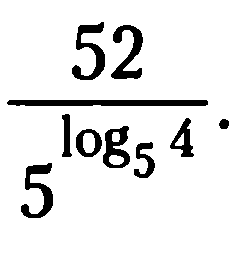
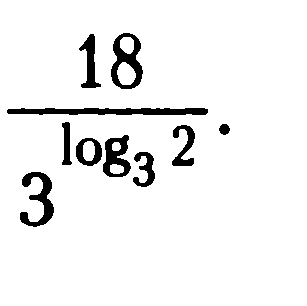
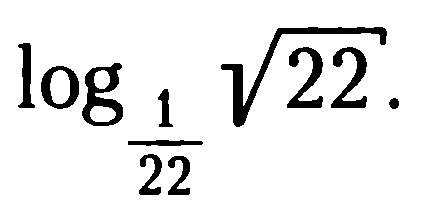
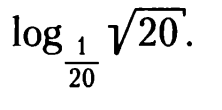

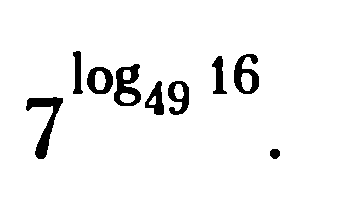
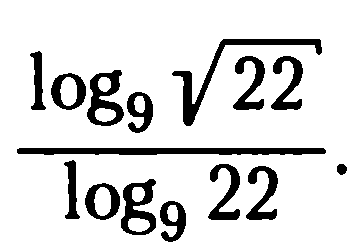
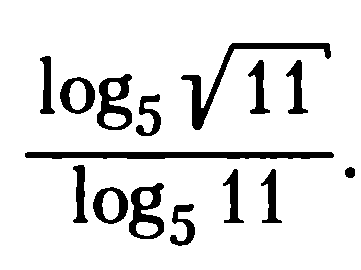
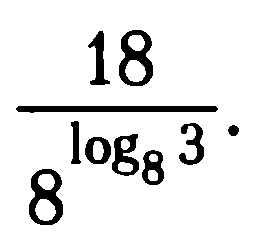
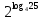
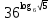
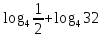
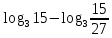
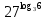
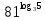
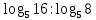
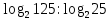
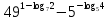
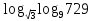
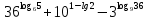
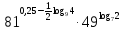
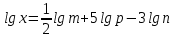
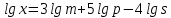
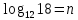
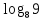
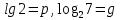
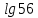
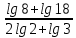
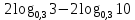
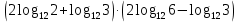
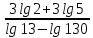
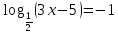
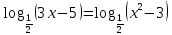
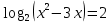
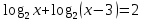
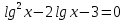
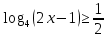
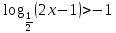
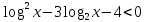
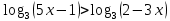
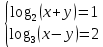
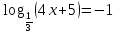
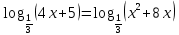
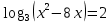
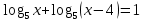
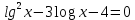
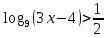
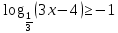
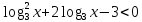
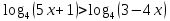

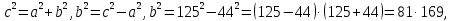 (второй катет равен 100 - 56 = 44 ).b =
(второй катет равен 100 - 56 = 44 ).b = 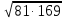 = 9
= 9 см. Ответ: 117 см
см. Ответ: 117 см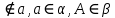
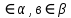
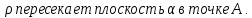
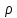 и параллельная плоскости
и параллельная плоскости 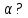
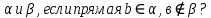
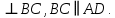 Будет ли прямая MN
Будет ли прямая MN 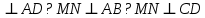 ?
?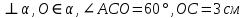 . Найти:
. Найти: 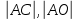
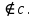 Провести через точку В плоскость
Провести через точку В плоскость 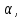 перпендикулярную прямой с.
перпендикулярную прямой с.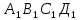 - куб. Доказать, что ВД
- куб. Доказать, что ВД 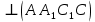 .
.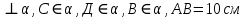 ,
, 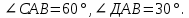 Найти:
Найти: 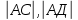
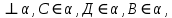 АВ = 20 см,
АВ = 20 см, 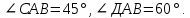 Найти:
Найти: 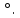 Найдите длину наклонной.
Найдите длину наклонной. а угол между их проекциями - прямой. Найдите расстояние от данной точки до плоскости.
а угол между их проекциями - прямой. Найдите расстояние от данной точки до плоскости.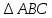 , А
, А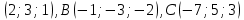
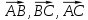
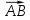
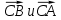
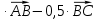
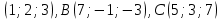
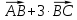
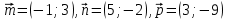
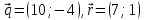
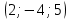 и В
и В 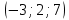
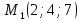 и
и