Методические указания по математике для специальностей СПО. Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине
 Скачать 471.38 Kb. Скачать 471.38 Kb.
|
Практическая работа № 18Решение простейших тригонометрических уравнений и неравенств различными способами. Цель: повторение изученного материала перед итоговой аттестацией. Пояснения к работе. 1. Рассмотрите п. 9 с.67 учебника « Алгебра и начала анализа 10 – 11», примеры 1 – 9, разобранные в этом пункте. 2. Вспомните формулы решения простейших тригонометрических уравнений. Задания к практической работе.
 Критерии оценки: Критерии оценки:«5» -ставится за все верно выполненные задания; «4» - за 1 и 2, 1 и 3, 1 и 4 верно выполненные задания; «3» - за 1 или за 2,3,4 верно выполненные задания; «2» - во всех остальных случаях. Литература. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. Раздел 4. Функции и графики. Тема 4.1. Свойства функции. Практическая работа № 19 Решение задач методом интервалов Цель: способствовать закреплению навыков решения задач методом интервалов. Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 5 шагов: Решить уравнение f (x) = 0. Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов. Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней. Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется. Выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имеет вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0. . Задания к практической работе.
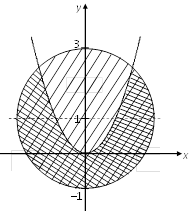
Критерии оценки: «5» - ставится за 5 верно решенных заданий; «4» - ставится за 4 верно решенных задания; «3» - ставится за 3 верно решенных задания; «2» - если решено менее 3 заданий. Литература. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. Тема 4.1. Свойства функции. Практическая работа № 20 Графическое решение систем неравенств нескольких переменных. Цель: способствовать закреплению навыков решения систем неравенств нескольких переменных. Системы, содержащие неравенства с двумя переменными, вида 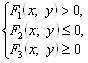 Называются системами неравенств с двумя переменными. Решением данных систем является пересечение решений всех неравенств, входящих в систему. Пример 1. Решить систему Решение.Построим в системе Оху соответствующие линии
Уравнение определяет параболу с вершиной в точке О(0; 0). Найдем решения каждого из неравенств, входящих в систему. Первому неравенству соответствует область внутри окружности и сама окружность (в справедливости этого убеждаемся, если подставим в неравенство координаты любой точки из этой области). Второму неравенству соответствует область, расположенная под параболой. Решение системы – пересечение двух указанных областей (на рисунке показано наложением двух штриховок). Задания к практической работе.
Критерии оценки: «5» - ставится за 5 верно выполненных заданий; «4» - ставится за 4 верно сделанных задания; «3» - ставится за 3 верно выполненных задания; «2» - если решено менее 3 заданий. Литература. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014. РАЗДЕЛ 5 ГЕОМЕТРИЯ ТЕМА5.1. Многогранники. Практическая работа № 21 Параллелепипед. Куб. Цель: закрепление знаний, отработка навыков решения задач, используя свойства пирамиды и куба. Пояснения к работе: 1. Изучите п. 172 - 175(с. 301 ), учебника Геометрия 7 – 1 Погорелова А. В.. 2. Сделайте краткий конспект ( чертежи, основные определения, формулы) 3. Рассмотрите решение задачи: № 22 стр.301 4. Запомните свойства параллелепипеда: 1. У параллелепипеда противолежащие грани равны и параллельны. 2) Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам. 3) В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений. 4) У куба все грани – равные между собой квадраты. Задания к практической работе.
Критерии оценки: «5» - ставится за три верно решенные задачи; «4» - ставится за две верно решенные задачи; «3» - ставится за одну верно решенную задачу; «2» - менее одной задачи. Литература. Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил. ТЕМА 5.2. Многогранники. Практическая работа № 22. Пирамида. Правильная пирамида. Усеченная пирамида. Тетраэдр. Цель: закрепление знаний, отработка навыков решения задач, используя свойства пирамиды. Пояснения к работе: 1. Изучите п. 176 (с. 305 ), 177, 178, 179 учебника Геометрия 7 – 11 Погорелова А. В.. 2. Сделайте краткий конспект ( чертежи, основные определения, формулы) 3. Рассмотрите решение задачи: № 69 стр.309 4. Запомните свойства пирамиды:1) Пирамида называется правильной , если ее основание есть правильный многоугольник и ее высота проходит через центр этого многоугольника. 2) В правильной пирамиде все боковые ребра равны между собой. 3) Все боковые грани правильной пирамиды – равные равнобедренные треугольники. Задания к практической работе.
Критерии оценки: «5» - ставится за три верно решенные задачи; «4» - ставится за две верно решенные задачи; «3» - ставится за одну верно решенную задачу; «2» - менее одной задачи. Литература. Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил. |

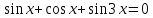 ;
;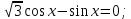
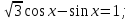
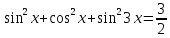
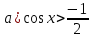 ;
; 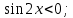
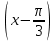
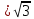 .
.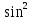 x –
x – 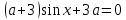 не имеет решений?
не имеет решений?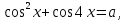
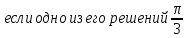 .
.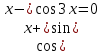 ;
; 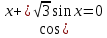 ;
;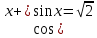 ;
;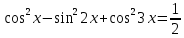
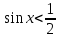 ;
;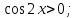
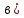 ctg
ctg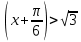
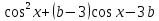 = 0 не имеет решений?
= 0 не имеет решений?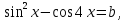 если одно из его решений
если одно из его решений 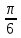 .
.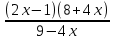 ≥ 0
≥ 0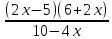 ≥ 0
≥ 0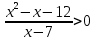
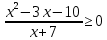
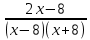
 0
0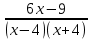
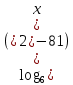
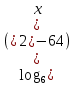
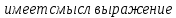
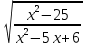 ?
?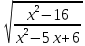 ?
?
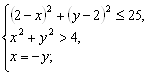
 . Найдите высоту пирамиды, если стороны основания равны 20, 21 и 29 см.
. Найдите высоту пирамиды, если стороны основания равны 20, 21 и 29 см.