Методические рекомендации
по суммативному оцениванию
Геометрия
8 класс
Методические рекомендации составлены в помощь учителю при планировании, организации и проведении суммативного оценивания за раздел по предмету «Геометрия» для обучающихся 8 классов. Методические рекомендации подготовлены на основе типовой учебной программы и учебного плана.
Задания для суммативного оценивания за раздел позволят учителю определить уровень достижения обучающимися целей обучения, запланированных на четверть.
Для проведения суммативного оценивания за раздел в методических рекомендациях предлагаются задания, критерии оценивания с дескрипторами и баллами. Также в сборнике описаны возможные уровни учебных достижений обучающихся (рубрики). Задания с дескрипторами и баллами носят рекомендательный характер.
Методические рекомендации предназначены для учителей, администрации школ, методистов отделов образования, школьных и региональных координаторов по критериальному оцениванию и других заинтересованных лиц.
При подготовке методических рекомендаций использованы ресурсы (рисунки, фотографии, тексты, видео- и аудиоматериалы и др.), находящиеся в открытом доступе на официальных интернет-сайтах.
Содержание
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ 4
Суммативное оценивание за раздел 4
«Многоугольники. Исследование четырехугольников» 4
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ 7
Суммативное оценивание за раздел 7
«Соотношения между сторонами и углами прямоугольного треугольника» 7
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ 10
Суммативное оценивание за разде «Площадь» 10
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ 13
Суммативное оценивание за раздел 13
«Прямоугольная система координат на плоскости» 13
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ Суммативное оценивание за раздел «Многоугольники. Исследование четырехугольников» |
Тема
|
Многоугольник. Выпуклый многоугольник
Параллелограмм, ромб, прямоугольник, квадрат, их свойства и признаки
Трапеция, виды и свойства. Средние линии трапеции и треугольника
Замечательные точки треугольника
|
Цель обучения
|
8.1.1.2 Выводить формулы суммы внутренних углов и суммы внешних углов многоугольника
8.1.1.4 Выводить и применять свойства параллелограмма
8.1.1.5 Выводить и применять признаки параллелограмма
8.1.1.12 Доказывать и применять свойство средней линии треугольника
8.1.3.1 Знать и применять свойства медиан, биссектрис, высот и серединных перпендикуляров к сторонам треугольника
|
Критерий оценивания
|
Обучающийся
Применяет формулы суммы внутренних углов и суммы внешних углов многоугольника
Применяет свойства и признаки параллелограмма при решени задач
Решает задачи, используя свойство средней линии треугольника
Применяет свойство медиан треугольника
|
Уровень мыслительных навыков
|
Применение
Навыки высокого порядка
|
Время выполнения
|
25 минут
|
Задания
1. а) Существует ли выпуклый четырехугольник, углы которого равны 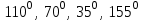 . Ответ обоснуйте. . Ответ обоснуйте.
b) Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 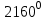 . .
2. В параллелограмме МKNZдиагонали пересекаются в точке О. Докажите, что четырехугольник ABCD, вершинами которого являются середины отрезков OM, OK, ONи OZ – параллелограмм.
3. Средняя линия треугольника отсекает от него трапецию с боковыми сторонами 5 м и 6 м и меньшим основанием 7 м. Найдите периметр треугольника.
4. В треугольнике АВС, АВ = АС. Медиана к боковой стороне делит высоту, проведённую к основанию, на отрезки, больший из которых равен 8. Найдите длину этой высоты.
|
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Применяет формулы суммы внутренних углов и суммы внешних углов многоугольника.
|
1
|
делает вывод о существовании многоугольника с заданной суммой углов;
|
1
|
обосновывает ответ;
|
1
|
применяет формулу суммы углов многоугольника;
|
1
|
вычисляет число сторон многоугольника;
|
1
|
Применяет свойства и признаки параллелограмма при решени задач.
|
2
|
выполняет рисунок по условию задачи;
|
1
|
применяет теорему о средней линии треугольника;
|
1
|
применяет свойство параллелограмма;
|
1
|
применяет признак параллелограмма;
|
1
|
Решает задачи, используя свойство средней линии треугольника.
|
3
|
определяет длины боковых сторон треугольника;
|
1
|
определяет длину основания треугольника;
|
1
|
находит периметр треугольника;
|
1
|
Применяет свойство медиан треугольника
|
4
|
выполняет рисунок по условию задачи;
|
1
|
применяет свойство равнобедренного треугольника;
|
1
|
применяет свойство медианы треугольника;
|
1
|
находит длину высоты.
|
1
|
Итого:
|
15
|
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Многоугольники. Исследование четырехугольников»
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Применяет формулы суммы внутренних углов и суммы внешних углов многоугольника
|
З атрудняется в применении формул суммы углов многоугольника атрудняется в применении формул суммы углов многоугольника
|
Д опускает ошибки при применении формулы суммы внутренних / внешних углов многоугольника / вычислительные ошибки опускает ошибки при применении формулы суммы внутренних / внешних углов многоугольника / вычислительные ошибки
|
В ычисляет градусные меры углов, применяя формулы суммы внутренних углов и суммы внешних углов многоугольника ычисляет градусные меры углов, применяя формулы суммы внутренних углов и суммы внешних углов многоугольника
|
Применяет свойства и признаки параллелограмма при решени задач
|
З атрудняется в применении свойств и признаков параллелограмма атрудняется в применении свойств и признаков параллелограмма
|
Д опускает ошибки при использовании свойств / признаков параллелограмма опускает ошибки при использовании свойств / признаков параллелограмма
|
Р ешает задачи, применяя свойства и признаки параллелограмма ешает задачи, применяя свойства и признаки параллелограмма
|
Решает задачи, используя свойство средней линии треугольника
|
З атрудняется в применении свойства средней линии треугольника атрудняется в применении свойства средней линии треугольника
|
И спользует свойство средней линии треугольника, допускает вычислительные ошибки спользует свойство средней линии треугольника, допускает вычислительные ошибки
|
 Применяет свойство средней линии треугольника при решении задач Применяет свойство средней линии треугольника при решении задач
|
Применяет свойство медиан треугольника
|
З атрудняется в применении свойства медиан треугольника атрудняется в применении свойства медиан треугольника
|
П рименяет свойство медиан треугольника, допускает вычислительные ошибки рименяет свойство медиан треугольника, допускает вычислительные ошибки
|
Р ешает задачи, применяя свойство медиан треугольника ешает задачи, применяя свойство медиан треугольника
| ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ Суммативное оценивание за раздел «Соотношения между сторонами и углами прямоугольного треугольника» |
Тема
|
Тригонометрические функции острого угла в прямоугольном треугольнике. Теорема Пифагора
Основные тригонометрические тождества
Решение прямоугольных треугольников
|
Цель обучения
|
8.1.3.2 Знать определения синуса, косинуса, тангенса и котангенса углов через отношения сторон в прямоугольном треугольнике
8.1.3.3 Доказывать и применять теорему Пифагора
8.1.3.24 Находить значения 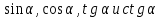 по данному значению одного из них по данному значению одного из них
8.1.3.8 Находить стороны и углы прямоугольного треугольника по двум заданным элементам
|
Критерий оценивания
|
Обучающийся
Определяет синус, косинус, тангенс и котангенс углов через отношения сторон в прямоугольном треугольнике
Решает задачи с помощью теоремы Пифагора
Находит значения тригонометрических функций по данному значению одной из них
Решает прямоугольный треугольник
|
Уровень мыслительных навыков
|
Применение
|
Время выполнения
|
25 минут
|
Задания
1. Дан прямоугольный треугольник МNР с прямым углом Р. Установите соответствия между отношениями сторон и тригонометрическими функциями острого угла:
а)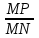 ; b) ; b) 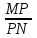 ; c) ; c) 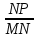 . .
1) синус угла М;
2) косинус угла М;
3) синус угла N;
4) косинус угла N;
5) тангенс угла М;
6) тангенс угла N;
7) котангенс угла М;
8) котангенс угла N.
2. Два туриста одновременно вышли из лагеря. Первый шел на север со скоростью 5 км/ч, второй шел на запад со скоростью 4 км/ч. Каким будет расстояние между ними через 4 часа.
3. Для острого угла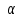 найдите найдите 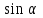 , ,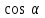 и и 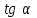 , если , если 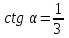 . .
4. Вертикальная башня высотой 40 м видна из точки К на поверхности земли под углом 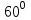 Найдите расстояния от точки К до основания башни и до самой высокой точки башни. Найдите расстояния от точки К до основания башни и до самой высокой точки башни.
|
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Определяет синус, косинус, тангенс и котангенс углов через отношения сторон в прямоугольном треугольнике
|
1
|
определяет соответствие для 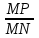 ; ;
|
1
|
определяет соответствие для 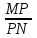 ; ;
|
1
|
определяет соответствие для 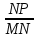 ; ;
|
1
|
Решает задачи с помощью теоремы Пифагора
|
2
|
определяет расстояние, пройденное каждым туристом;
|
1
|
применяет теорему Пифагора;
|
1
|
находит искомое расстояние;
|
1
|
Находит значения тригонометрических функций по данному значению одной из них
|
3
|
определяет значение 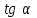 ; ;
|
1
|
применяет соотношение для нахождения 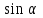 ; ;
|
1
|
находит 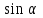 ; ;
|
1
|
применяет соотношение для нахождения 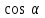 ; ;
|
1
|
находит 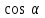 ; ;
|
1
|
Решает прямоугольный треугольник
|
4
|
выполняет рисунок по условию задачи;
|
1
|
применяет соотношение для нахождения расстояния от точки К до основания башни;
|
1
|
находит расстояние от точки К до основания башни;
|
1
|
применяет соотношение для нахождения расстояния от точки К до самой высокой точки башни;
|
1
|
находит расстояние от точки К до самой высокой точки башни.
|
1
|
Итого:
|
16
|
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Соотношения между сторонами и углами прямоугольного треугольника»
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Определяет синус, косинус, тангенс и котангенс углов через отношения сторон в прямоугольном треугольнике
|
Затрудняется в определении тригонометрических функций через отношения сторон в прямоугольном треугольнике

|
Допускает ошибки при определении синуса/ косинуса/ тангенса угла

|
 Определяет тригонометрические функции через отношения сторон в прямоугольном треугольнике Определяет тригонометрические функции через отношения сторон в прямоугольном треугольнике
|
Решает задачи с помощью теоремы Пифагора
|
З атрудняется в применении теоремы Пифагора атрудняется в применении теоремы Пифагора
|
П рименяет теорему Пифагора. Допускает вычислительные ошибки рименяет теорему Пифагора. Допускает вычислительные ошибки
|
П рименяет теорему Пифагора рименяет теорему Пифагора
|
Находит значения тригонометрических функций по данному значению одной из них
|
З атрудняется в нахождении значений тригонометрических функций по данному значению одной из них атрудняется в нахождении значений тригонометрических функций по данному значению одной из них
|
З аписывает соотношения для нахождения тригонометрических функций. Допускает вычислительные ошибки аписывает соотношения для нахождения тригонометрических функций. Допускает вычислительные ошибки
|
Н аходит значения тригонометрических функций по данному значению одной из них аходит значения тригонометрических функций по данному значению одной из них
|
Решает прямоугольный треугольника
|
Затрудняется в нахождении сторон и углов прямоугольного треугольника по двум заданным элементам

|
П рименяет верные соотношения для нахождения сторон и углов прямоугольного треугольника. Допускает вычислительные ошибки рименяет верные соотношения для нахождения сторон и углов прямоугольного треугольника. Допускает вычислительные ошибки
|
Н аходит стороны и углы прямоугольного треугольника по двум заданным элементам аходит стороны и углы прямоугольного треугольника по двум заданным элементам
| ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ Суммативное оценивание за разде «Площадь» |
Тема
|
Площадь фигуры и ее свойства
Площади четырёхугольников и треугольников
|
Цель обучения
|
8.1.3.10 Знать определения равновеликих и равносоставленных фигур
8.1.3.12 Выводить и применять формулы площади треугольника
8.1.3.13 Выводить и применять формулы площади трапеции
|
Критерий оценивания
|
Обучающийся
Применяет определения равновеликих и равносоставленных фигур
Применяет формулы площади треугольника
Применяет формулы площади трапеции
|
Уровень мыслительных навыков
|
Применение
|
Время выполнения
|
25 минут
|
Задания
1. Стороны прямоугольника равны 7 см и 18 см.
а) Найдите ширину прямоугольника, равновеликого данному, если его длина равна 14 см.
b) В каждом из этих прямоугольников провели диагональ. Будут ли они равносоставленными? Ответ обоснуйте.
[3]
2. В треугольнике МРК, 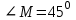 , а высота РН делит сторону МК на отрезки МН и НК соответственно равные 5 см и 8 см. Найдите площадь треугольника МРК. , а высота РН делит сторону МК на отрезки МН и НК соответственно равные 5 см и 8 см. Найдите площадь треугольника МРК.
[5]
3. В прямоугольной трапеции диагональ является биссектрисой острого угла. Найдите площадь трапеции, если боковые стороны равны 8 см и 10 см.
[7]
|
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Применяет определения равновеликих и равносоставленных фигур
|
1
|
применяет определение равновеликих фигур;
|
1
|
определяет сторону прямоугольника;
|
1
|
определяет равносоставленность прямоугольников и обосновывает свой ответ;
|
1
|
Применяет формулы площади треугольника
|
2
|
выполняет рисунок по условию задачи;
|
1
|
определяет вид треугольника МРН;
|
1
|
находит сторону МК треугольника МРК;
|
1
|
находит высоту треугольника МРК;
|
1
|
находит искомую площадь;
|
1
|
Применяет формулы площади трапеции
|
3
|
выполняет рисунок по условию задачи;
|
1
|
определяет вид треугольника, образованного диагональю, меньшим основанием и большей боковой стороной;
|
1
|
находит меньшее основание и равный ему отрезок большего основания;
|
1
|
применяет теорему Пифагора;
|
1
|
находит большее основание;
|
1
|
применяет формулу площади трапеции;
|
1
|
находит площадь трапеции.
|
1
|
Итого:
|
15
|
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Площади»
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Применяет определения равновеликих и равносоставленных фигур
|
З атрудняется в применении определения равновеликих и равносоставленных фигур атрудняется в применении определения равновеликих и равносоставленных фигур
|
П рименяет определение равновеликих фигур. Допускает ошибки в обосновании равносоставленности фигур рименяет определение равновеликих фигур. Допускает ошибки в обосновании равносоставленности фигур
|
Р ешает задачи, применяя определения равновеликих и равносоставленных фигур ешает задачи, применяя определения равновеликих и равносоставленных фигур
|
Применяет формулы площади треугольника
|
З атрудняется в применении формул площади треугольника атрудняется в применении формул площади треугольника
|
П рименяет формулы площади треугольника. Допускает вычислительные ошибки рименяет формулы площади треугольника. Допускает вычислительные ошибки
|
 Решает задачи на применение формул площади треугольника Решает задачи на применение формул площади треугольника
|
Применяет формулы площади трапеции
|
З атрудняется в применении формул площади трапеции атрудняется в применении формул площади трапеции
|
П рименяет формулы площади трапеции. Допускает вычислительные ошибки рименяет формулы площади трапеции. Допускает вычислительные ошибки
|
Р ешает задачи на применение формул площади трапеции ешает задачи на применение формул площади трапеции
|
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ Суммативное оценивание за раздел «Прямоугольная система координат на плоскости» |
Тема
|
Метод координат на плоскости
Решение текстовых задач
|
Цель обучения
|
8.1.3.14 Вычислять расстояние между двумя точками на плоскости по их координатам
8.1.3.15 Находить координаты середины отрезка
8.1.3.17 Знать уравнение окружности с центром в точке (a,b) и радиусом r: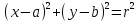
8.1.3.18 Строить окружность по заданному уравнению
8.1.3.20 Решать простейшие задачи в координатах
|
Критерий оценивания
|
Обучающийся
Применяет соотношения между координатами середины и координатами концов отрезка
Составляет уравнение окружности
Строит окружность по заданному уравнению
Решает простейшие задачи в координатах
|
Уровень мыслительных навыков
|
Применение
|
Время выполнения
|
25 минут
|
Задания
1. Точка Т – середина отрезка МР. Найдите координаты точки Р, если Т(-3;4) и М(-5;-7).
2.
a) АВ – диаметр окружности с центром О. Найдите координаты центра окружности, если А(7;-2) и В(-1;-4).
b) Запишите уравнение окружности, используя условия пункта а).
3. Выполнив построение, выясните взаимное расположение двух окружностей, заданных уравнениями 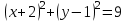 и и 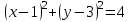
4. Точки А(-9;1), В(-1;5), С(8;2), D(-6;-5) – вершины прямоугольной трапеции с основаниями АВ и CD. Найдите длину средней линии и площадь трапеции.
|
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Применяет соотношения между координатами середины и координатами концов отрезка
|
1
|
выражает координаты конца отрезка через координаты середины и координаты другого конца отрезка;
|
1
|
находит координаты точки;
|
1
|
2а
|
выражает координаты середины отрезка через координаты его концов;
|
1
|
находит координаты центра окружности;
|
1
|
Составляет уравнение окружности
|
2b
|
определяет радиус окружности;
|
1
|
записывает уравнение окружности;
|
1
|
Строит окружность по заданному уравнению
|
3
|
строит первую окружность;
|
1
|
строит вторую окружность;
|
1
|
делает вывод о взаимном расположении двух окружностей;
|
1
|
Решает простейшие задачи в координатах
|
4
|
находит координаты середин боковых сторон или длины оснований трапеции;
|
1
|
находит среднюю линию;
|
1
|
находит длины боковых сторон;
|
1
|
определяет, какая из боковых сторон является высотой;
|
1
|
находит площадь трапеции.
|
1
|
Итого:
|
14
|
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
«Прямоугольная система координат на плоскости»
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Применяет соотношения между координатами середины и координатами концов отрезка
|
З атрудняется в применении соотношений между координатами середины и координатами концов отрезка атрудняется в применении соотношений между координатами середины и координатами концов отрезка
|
П рименяет соотношения между координатами середины и координатами концов отрезка. Допускает вычислительные ошибки рименяет соотношения между координатами середины и координатами концов отрезка. Допускает вычислительные ошибки
|
Р ешает задачи, применяя соотношения между координатами середины и координатами концов отрезка ешает задачи, применяя соотношения между координатами середины и координатами концов отрезка
|
Составляет уравнение окружности
|
З атрудняется в составлении уравнения окружности атрудняется в составлении уравнения окружности
|
Подставляет компоненты в уравнение окружности. Допускает ошибки со знаками / вычислительные ошибки

|
С оставляет уравнение окружности оставляет уравнение окружности
|
Строит окружность по заданному уравнению
|
З атрудняется в построении окружности по заданному уравнению атрудняется в построении окружности по заданному уравнению
|
О пределяет координаты центра и радиус окружности. Допускает погрешности в построении пределяет координаты центра и радиус окружности. Допускает погрешности в построении
|
В ыполняет построение окружности по заданному уравнению ыполняет построение окружности по заданному уравнению
|
Решает простейшие задачи в координатах
|
З атрудняется в решении простейших задач в координатах атрудняется в решении простейших задач в координатах
|
П рименяет соответствующие формулы. Допускает вычислительные ошибки рименяет соответствующие формулы. Допускает вычислительные ошибки
|
Р ешает простейшие задачи в координатах ешает простейшие задачи в координатах
| |
 Скачать 129.24 Kb.
Скачать 129.24 Kb.
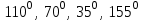 . Ответ обоснуйте.
. Ответ обоснуйте.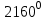 .
. атрудняется в применении формул суммы углов многоугольника
атрудняется в применении формул суммы углов многоугольника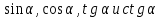 по данному значению одного из них
по данному значению одного из них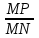 ; b)
; b) 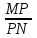 ; c)
; c) 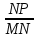 .
.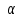 найдите
найдите 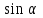 ,
,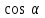 и
и 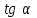 , если
, если 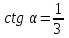 .
.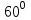 Найдите расстояния от точки К до основания башни и до самой высокой точки башни.
Найдите расстояния от точки К до основания башни и до самой высокой точки башни.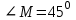 , а высота РН делит сторону МК на отрезки МН и НК соответственно равные 5 см и 8 см. Найдите площадь треугольника МРК.
, а высота РН делит сторону МК на отрезки МН и НК соответственно равные 5 см и 8 см. Найдите площадь треугольника МРК.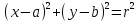
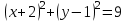 и
и