практика. Методические указания для выполнения практических работявляются частью программы подготовки специалистов среднего звена гбпоу ро Миллеровский техникум агропромышленных технологий и управления
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
Тема: Абсолютные и относительные величины в статистике. Название практического занятия: Расчет абсолютных и относительных показателей вариации Цель занятия: освоить методику расчета абсолютных и относительных показателей вариации Оснащение рабочего места: схемы, канцелярские принадлежности, калькулятор Время выполнения задания: 2 часа. I Контрольные вопросы. 1) В чем сущность средней величины, как статистического показателя? 2) Что представляет собой средняя величина? 3) Как исчисляется средняя арифметическая для интервального ряда? 4) Для каких целей применяется средняя геометрическая и где она применяется? II Методическое обеспечение. Относительные показатели планового задания (ОППЗ) характеризуют отношение планируемого уровня показателя к фактически достигнутому уровню того периода, по сравнению с которым намечается увеличение или уменьшение показателей. ОППЗ=УРОВЕНЬ ПОКАЗАТЕЛЯ, ЗАПЛАНИРОВАННЫЙ НА ПРЕДСТОЯШИЙ ПЕРИОД (i+l) УРОВЕНЬ ПОКАЗАТЕЛЯ, ДОСТИГНУТЫЙ В ПРЕДЫДУЩЕМ ПЕРИОДЕ (i) Относительные показатели выполнения плана (ОПВП) используется для контроля за ходом выполнения планов субъектов финансово- хозяйственной деятельности. Они показывают соотношение между фактическим и плановым уровнями показателя и обычно выражаются в процентах. ОПВП= уровень, фактически достигнутый в отчетном периоде *100% Уровень, запланированный на отчетный период Относительными величинами динамики (ОВД) – ТЕМПАМИ РОСТА – называется показатели, характеризующие изменение величины общественных явлений во времени. Этот вид относительных величин широко применяется в планировании, анализе и статистике. ОВД= ТЕКУЩИЙ ПОКАЗАТЕЛЬ ПРЕДШЕДСТВУЮЩИЙ ИЛИ БАЗИСНЫЙ ПОКАЗАТЕЛЬ Относительные величины динамики выражаются либо в коэффициентах, либо в процентах. При вычислении относительной величины динамики за базу (100%) может приниматься все время одна величина. Такие величины называются относительными величинами с постоянной базой. Они применяются в тех случаях, когда есть необходимость постоянного наблюдения за развитием изучаемых явлений по сравнению с периодом, имеющим почему- либо особо важное для подобного сравнения знания. В случае необходимости выяснения темпов развития, интересующего нас явления каждый показатель, сравнивается уже не с одной постоянной величиной, а со своей предыдущей, то есть за базу (100%) принимается показатель соседнего периода. Такие относительные величины динамики называется величинами, вычисленными цепным способом (каждый последующий период сопоставляется со своим предшествующим, и показатели динамики образуют как бы цепь). Относительные показатели структуры (ОПС) характеризует составные части совокупности. Относительная величина совокупности рассчитывается по формуле ОПС= уровень части совокупности_________________ *100% Суммарный уровень совокупности в целом Относительные величины структуры, обычно называемые удельными весами, рассчитываются делением определенной части целого на общий итог, принимаемый за 100%. У этой величины есть одна особенность- сумма относительных величин изучаемой совокупности всегда равна 100% или 1 (в зависимости от того, в чем она выражаются). Относительные величины структуры чаще всего выражается в процентах. Они применяются при изучении сложных явлений, распадающихся на ряд групп или частей, характеристики удельного веса (доли) каждой группы в общем итоге. Относительные показатели координации (ОПК) характеризуют соотношение отдельных частей совокупности с одной из них, принятой за базу сравнения. ОПК= Пn, Пб где Пn- показатель, характеризующий n-ю часть совокупности; Пб- показатель, характеризующий часть совокупности, выбранную в качестве базы сравнения. Относительными показателями интенсивности (ОПИ)называются показатели, определяющие степень распространенности данного явления в какой- либо среде. Они рассчитываются как отношение абсолютной величины данного явления к размеру среды, в которой оно развивается. ОПИ= Уровень, характеризующий явление А__________________ Уровень, характеризующий среду распространения явления А Относительные величины интенсивности вычисляются путем сопоставления разноименных абсолютных величин, находящихся в определенной связи друг с другом, и в отличие от других видов относительных величин являются обычно именованными числами и имеют размерность тех абсолютных величин, соотношение которых они выражают. Тем не менее в ряде случаев, когда полученные результаты расчетов слишком малы, их умножают для наглядности на 1000 или 10000, получая характеристики в промилле. Относительные показатели сравнения (ОПРс) получаются в результате деления одноименных абсолютных уровней, соответствующих одному и тому же периоду или моменту времени, но относящихся к различным объектам или территориям. ОПРс = Абсолютный показатель, характеризующий объект А Абсолютный показатель, характеризующий объект Б Обычно их исчисляют в процентах или кратных отношениях, показывающих, во сколько раз одна из сравниваемых величин больше (или меньше) другой. Это может быть, как отношение пространственного, так и отношение временного сравнения. III Порядок и последовательность выполнения задания. Задание 1. В январе отчетного года валовой доход фирмы, занимающейся производством и продажей сложной бытовой техники, составил 1500 тыс. руб., в феврале планируется товарооборот в 1800 тыс. руб. Определить относительную величину планового задания. Задание 2. Валовой доход фирмы, занимающейся производством и продажей сложной бытовой техники, в феврале отчетного года составил 2055,5 тыс. руб. при плане 1800 тыс. руб. Определить степень выполнения плана по валовому доходу фирмы в феврале текущего года. Задание 3. Рассчитайте цепные и базисные относительные величины динамики численности работников торгового предприятия за 2015-2018 гг. Таблица 2.1 - Динамика численности работников торгового предприятия за 2015-2018 гг.
Решение: Результаты расчетов занесем в таб. 2.2. Таблица 2.2 - Базисные и цепные относительные показатели динамики численности работников торгового предприятия
Анализ данных таблиц 2.2 показал, что за период с 2015 по 2018 г. наблюдался постепенный рост численности работников торгового предприятия. Задание 4. имеются следующие данные о розничном товарообороте предприятия за 2017-2018 гг., млн. руб.: Таблица 2.3. - Динамика розничного товарооборота предприятия по кварталам 2017-2018 гг.
Исчислить относительные величины структуры розничного товарооборота предприятия по кварталам за каждый год. Решение. Исчислим относительные величины структуры розничного товарооборота за 2017 и 2018 гг. d1=173.7 *100%=23.0% d1= 200.7 *100%=23.3% 753.3 862.6 и т.д. и т.д. Исчисленные относительные величины структуры товарооборота, представленные в табл.2.4. Таблица 2.4 - Структура розничного товарооборота предприятия по кварталам 2017-2018 гг.
Данные табл. 2.4. свидетельствуют о том, что в изучаемые годы удельный вес розничного товарооборота закономерно растет от 1 к 4 кварталу. Задание 5. Имеются следующие данные о численности экономически активного населения одного из городов области по состоянию на начало 2018 г., тыс. чел.: Численность экономически активного населения 125,1 в том числе: - занятых в экономике 96,4 - безработных 28,7 Исчислить, сколько безработных приходится на 1000 чел. занятого населения. Задание 6. Среднегодовая численность населения РФ в 2018 г. составила 145,2 млн. чел., число родившихся -1397 тыс. чел., число умерших- 2332,3 тыс. чел. Определить относительные величины интенсивности, характеризующие: а) рождаемость, б) смертность населения. Решение: а) коэффициент рождаемости = число родившихся * 1000. среднегодовая численность населения б) коэффициент смертности = число умерших *1000. Среднегодовая численность населения Задание 7. Численность населения в Российской Федерации в 2018 г. составило 145,2 млн. чел., в том числе: городское - 106,4 млн. чел.; сельского -3 8,7 млн. чел. Сравните численность городского и сельского населения страны, приняв за базу сравнения численность сельского населения. Форма отчета: завершить расчеты и оформить в тетрадь Методические указания по выполнению практической работы №5 учебная дисциплина ОП.12. Статистика специальность 38.02.01 Экономика и бухгалтерский учет (по отраслям) Тема: Средняя величина в статистике. Наименование занятия: Определение среднего уровня изучаемого явления и анализ полученных результатов Цель занятия: Определение среднего уровня изучаемого явления и анализ основание полученных результатов. Оснащение рабочего места: схемы, канцелярские принадлежности, калькулятор Время выполнения задания: 2 часа. I Контрольные вопросы. 1) В чем сущность средней величины, как статистического показатель? 2) Что представляет собой средняя величина? 3) Как исчисляется средняя арифметическая для интервального ряда? 4) Для каких целей применяется средняя геометрическая и где она применяется? II Методическое обеспечение. Средняя арифметическая простая: где x- индивидуальное значение признака. n- численность совокупности. Средняя арифметическая взвешенная: Средняя гармоническая простая: 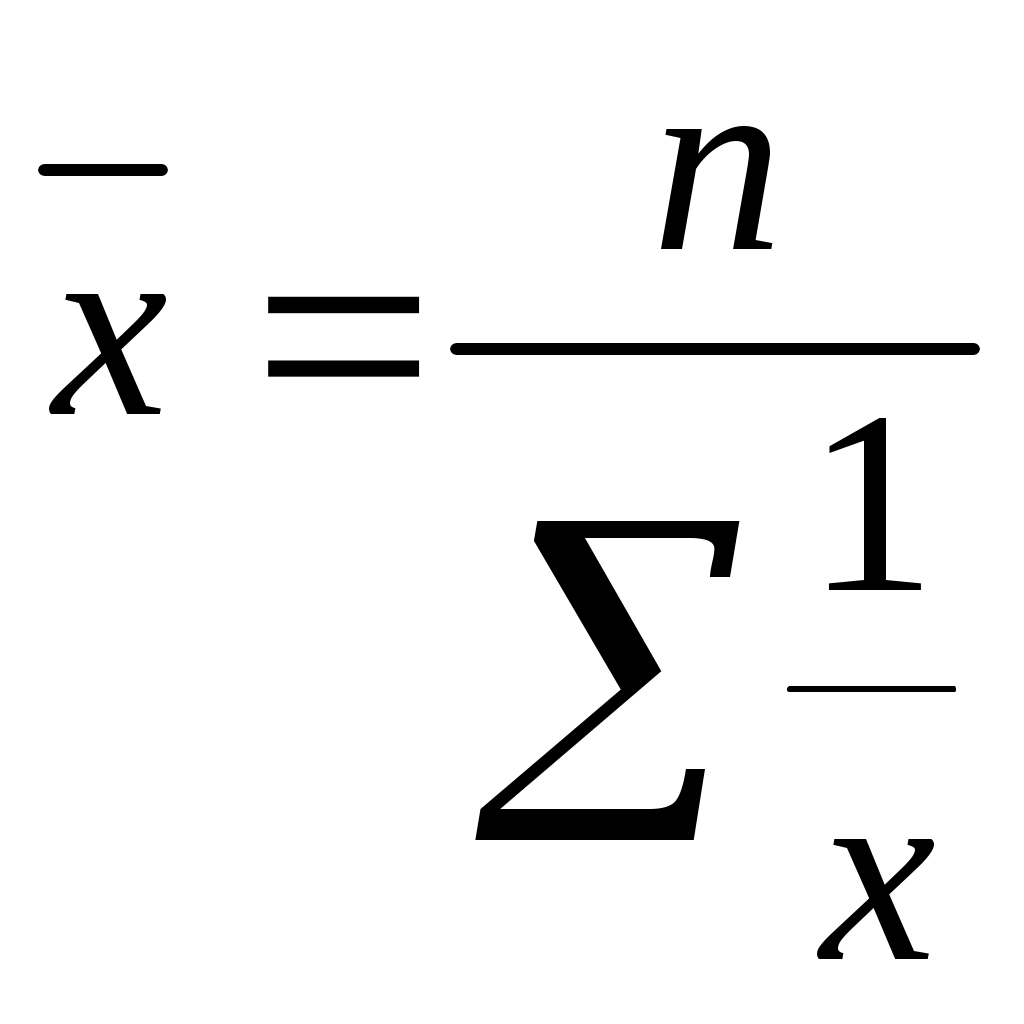 Средняя гармоническая взвешенная: 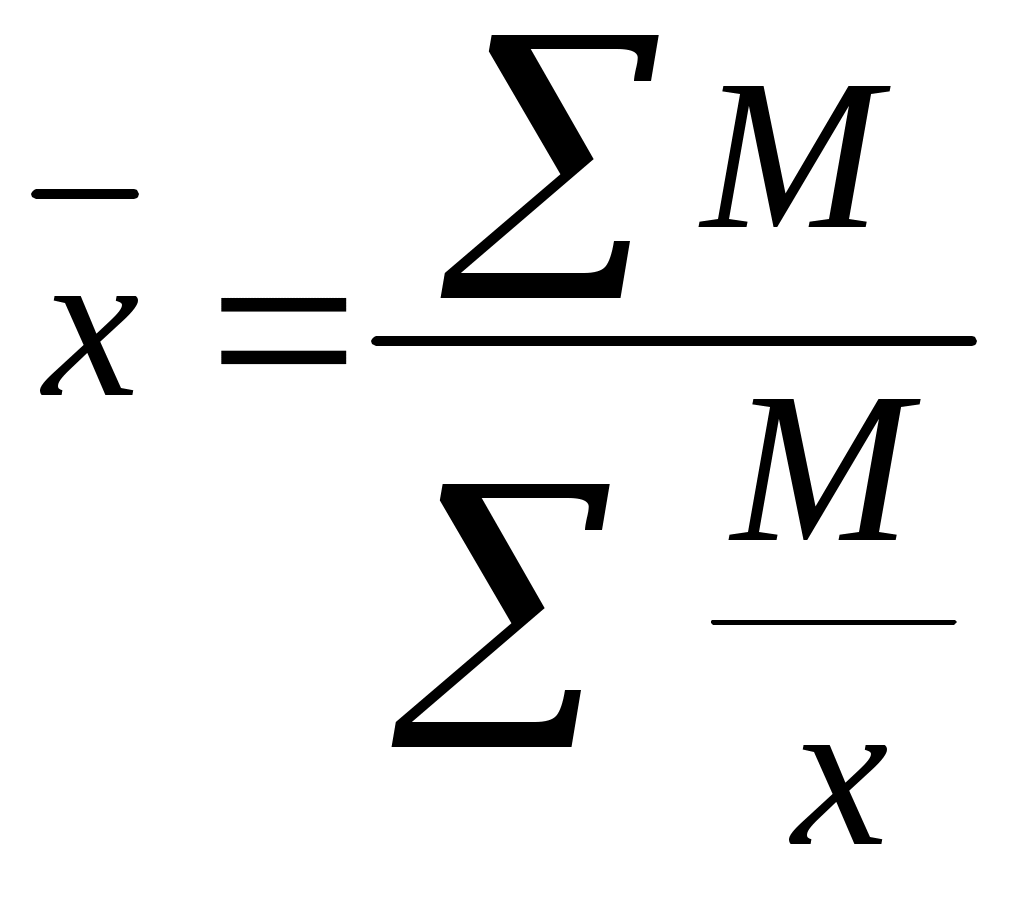 где М= x*f Средняя геометрическая простая: Средняя геометрическая взвешенная: П f- Продолжительность отрезков времени. Средняя квадратическая простая: Средняя квадратическая взвешенная: 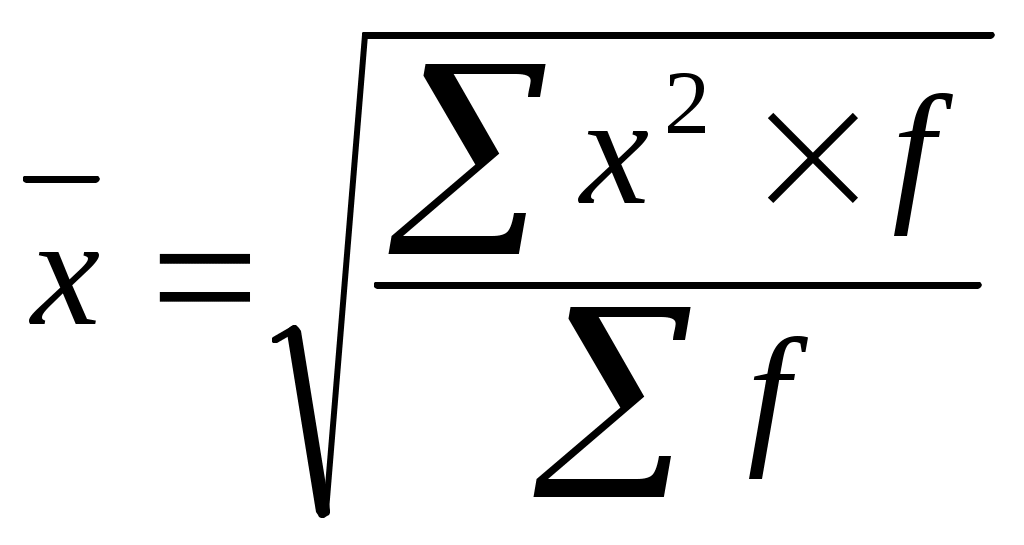 III Порядок и последовательность выполнения задания. Задание 1.
Рассчитать среднюю заработную плату рабочим в бригаде из 20 человек Задание 2
Определить средний товарооборот. Задание 3. Имеются данные урожайности по следующим регионам:
Определить среднюю урожайность яровой пшеницы используя среднюю гармоническую формулу IV. После выполнения задания студент обязан: Знать: - понятие о состоянии средних величинах. - виды средних величин. - методику их исчисления. - применение средних величин в статистической практике. Уметь: -исчислять средние величины статистических данных. V Задание на дом. Исчислить среднюю продукцию оборотных средств
Форма отчета: завершить расчеты и оформить в тетрадь Методические указания по выполнению практической работы №6 учебная дисциплина ОП.02. Статистика специальность 38.02.01 Экономика и бухгалтерский учет (по отраслям) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
