Механика. Механика - МУ и контрольные задания. Методические указания и контрольные задания для студентов заочной формы обучения Астрахань 2022 у дк 531. 8
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
|
РАЗДЕЛ 2. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ Введение В разделе «Сопротивление материалов» рассматриваются инженерные методы расчета отдельных элементов конструкций на прочность, жесткость и устойчивость. Конструкция считается прочной, если размеры каждого ее элемента подобраны так, что способны воспринимать заданную нагрузку, не разрушаясь, с учетом требуемого времени работы. Жесткость конструкции обеспечивается, если под действием заданной нагрузки деформации не превышают допускаемые пределы. Конструкция считается устойчивой, если она сохраняет первоначальную форму упругого равновесия при действии внешних нагрузок. Использование указанных методов расчета должно обеспечивать надежность работы конструкции и сочетаться с принципом экономичности ее изготовления и эксплуатации. В сопротивлении материалов рассматривают типичные элементы конструкций: брус (стержень, балка, вал), пластина, оболочка. Внешние нагрузки, действующие на элементы сооружений, подразделяют на сосредоточенные и распределенные, статические и динамические. Все реальные силы - это силы, распределенные по некоторой площади или объему. Однако распределенную нагрузку на небольшой площади, размеры которой очень малы по сравнению с размерами всего элемента, можно заменить сосредоточенной равнодействующей силой, что упростит расчет. Распределенные нагрузки имеют размерность единицы силы, отнесенной к единице длины или к единице поверхности или объема. Статическими нагрузками считают те, которые нагружают конструкции постепенно, и, будучи приложены к сооружению, они не меняются или меняются во времени незначительно. При действии статических нагрузок на конструкцию все ее части находятся в равновесии; ускорения, элементов конструкции отсутствуют или настолько малы, что ими можно пренебречь. Если же эти ускорения значительны, т. е. изменение скорости движения элементов машины происходит за сравнительно небольшой период времени, то мы имеем дело с приложением динамических нагрузок. Примерами таких нагрузок могут служить внезапно приложенные нагрузки, ударные и повторно-переменные. Действие таких нагрузок сопровождается возникновением колебаний конструкций или сооружений. Вследствие изменения скорости колеблющихся масс возникают силы инерции, пропорциональные (согласно второму закону Ньютона) колеблющимся массам и ускорениям. Методы расчета элементов конструкций излагаются на основе следующих упрощений и допущений: материал тела имеет сплошное (непрерывное) строение, т. е. не принимается во внимание дискретная атомарная структура вещества; принимается, что материал тела однороден, т. е. обладает во всех точках одинаковыми свойствами; материал тела изотропен, когда он обладает во всех направлениях одинаковыми свойствами; предполагается, что в теле до приложения нагрузки нет внутренних (начальных) усилий; что результат действия на тело системы сил равен сумме результатов действия тех же сил, прилагаемых к телу последовательно и в любом порядке. Для лучшего усвоения пройденного материала после изучения каждой темы необходимо ответить на вопросы для самопроверки, приведенные в методических указаниях. 1. Растяжение и сжатие В природе различают упругое, упругопластичное и вязкопластичное твердые тела. Упругое тело после снятия внешней нагрузки восстанавливает свои первоначальные размеры и форму. В этом случае деформация тела называется упругой. Упругопластичное тело восстанавливает свои первоначальные размеры и формы не полностью, т. е. имеет место остаточная деформация. В строительных сооружениях и машинах недопустимо появление остаточных деформаций. От действия внешних нагрузок в поперечных сечениях возникают внутренние силовые факторы, которые определяют, используя метод сечений. Твердое тело, находящееся под действием внешних нагрузок, мысленно рассекают на две части и рассматривают равновесие одной из частей. Действие отброшенной части на оставшуюся заменяют внутренними нагрузками, приложенными в рассматриваемом сечении. Составляя уравнения равновесия оставшейся части тела, нагруженного внешними и внутренними силовыми факторами, находят последние. Важнейшими понятиями являются напряжения и деформации. При расчетах на прочность тела, нагруженного растягивающими или сжимающими силами, определяют напряжения, деформации и удлинения. Внутренние силы взаимодействия, отнесенные к единице площади сечения, выделенного в окрестности какой-либо точки поперечного сечения тела, называют напряжением в этой точке. Таким образом напряжение в каждой точке сечения является мерой внутренних сил, которые возникают в материале в результате действия внешних нагрузок. Напряжение σ в поперечных сечениях тела определяются из соотношения 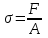 , ,где F - действующая в сечении сила; А - площадь поперечного сечения. Напряжения и деформации в пределах упругой области деформирования связаны между собой линейной зависимостью, называемой законом Гука. Аналитически эта связь может быть записана таким образом: 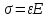 , ,где Е - модуль упругости первого рода; ε - относительная продольная деформация. Расчетные значения напряжения сравнивают с допускаемыми, которые определяются как отношение некоторых предельных значений напряжения σlim к некоторому числу s, называемому коэффициентом запаса прочности: 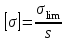 . .За предельные значения напряжений принимают предел прочности σв (для хрупких материалов) или предел текучести σТ (для пластичных материалов), которые определяются при испытаниях на растяжение стандартных образцов на разрывных машинах. При этом строят в координатах «напряжение - деформация» диаграмму растяжения, на которой напряжения и деформации вычисляют соответственно по отношению к первоначальной площади сечений и длине образца. Используя условную диаграмму растяжения, необходимо уметь определять механические характеристики материала: предел пропорциональности σпц; предел упругости σу; предел текучести σТ, предел прочности σв и остаточное удлинение Δlпри разрыве. Иногда для изучения значительных пластических деформаций необходимо знать истинную диаграмму растяжения, показывающую отношение растягивающей силы к истинной площади поперечного сечения образца с учетом уменьшения поперечных размеров сечения при растяжении. Необходимо усвоить, что закон Гука, связывающий напряжения и деформации через модуль упругости материала, справедлив только до предела пропорциональности. Продольные деформации при растяжении связаны с поперечными деформациями с помощью коэффициента Пуассона µ. При определении напряжений и деформаций в статически неопределимых системах необходимо учитывать, что возникающие при этом в стержнях силы зависят от жесткости стержня, т. е. от площади поперечных сечений и модулей упругости материала. В статически неопределимых системах необходимо также учитывать изменение температуры, так как это приводит к появлению внутренних сил. Вопросы для самопроверки 1. Какие тела называют упругими и упругопластичными? 2. В чем сущность метода сечений? 3. Что называют напряжением в данной точке сечения? 4. Какие напряжения называют нормальными? 5. Какие деформации являются упругими, а какие остаточными (пластическими)? 6. Как формулируется закон Гука? 7. Как определяют допустимые напряжения? 8. Что называют коэффициентом запаса прочности? 9. Каково условие прочности при растяжении? 10. Как строится диаграмма растяжения? 11. Почему диаграмма растяжения называется условной? 12. Что называют пределом прочности и пределом текучести материала? 13. Что называют относительным остаточным удлинением при разрыве? 14. Что называют истинной диаграммой растяжения? 15. Что называют коэффициентом Пуассона и чему он равен? 16. Какие системы называют статически неопределимыми? 17. Какие материалы называют хрупкими, а какие пластичными? 18. Как находят напряжения при изменении температуры? 2. Изгиб При изгибе брус, называемый балкой, подвергается воздействию поперечной силы или изгибающего момента. Изгиб называется чистым, если действует только изгибающий момент, и поперечным, если поперек стержня действует нормальная нагрузка, перпендикулярная оси стержня. Балки являются наиболее часто встречающимися элементами сооружений и машин, воспринимающими нагрузки от других элементов конструкций и передающими их тем частям, которые поддерживают балку (чаще всего опорам). В строительных сооружениях, машиностроительных конструкциях, приборах и т. д. чаще всего можно встретить следующие случаи закрепления концов балок: консольные - с одним защемленным концом (с жесткой заделкой), когда конец балки не может ни перемещаться, ни поворачиваться, двухопорные - с одной шарнирно-неподвижной опорой и с одной шарнирно-подвижной опорой и многоопорные балки. Если опорные реакции не могут быть найдены только из уравнений статики, такие балки называют статически неопределимыми. Для определения реакций в таких балках приходится составлять дополнительные уравнения - уравнения перемещений. При плоском поперечном изгибе все внешние нагрузки перпендикулярны оси балки. Определение внутренних силовых факторов, действующих в поперечных сечениях балки, следует начинать с определения опорных реакций. После этого используем метод сечений, для чего мысленно рассекаем балку на две части и рассматриваем равновесие одной из них. Взаимодействие ее с другой частью балки заменяем внутренними реакциями в виде изгибающего момента и поперечной силы. Поперечная сила в сечении равна алгебраической сумме проекций всех сил на ось, перпендикулярную оси балки, а изгибающий момент равен алгебраической сумме моментов всех сил, расположенных по одну сторону от сечения. Знаки действующих сил и моментов следует определять в соответствии с определенными правилами. Необходимо научиться правильно определять равнодействующую силу и изгибающий момент от равномерно распределенной по длине балки нагрузки. Следует иметь в виду, что при определении напряжений, возникающих при изгибе, принимают следующие допущения: сечения балки плоские до изгиба остаются плоскими и после изгиба (гипотеза плоских сечений); продольные соседние волокна не давят одно на другое; зависимость между напряжениями и деформациями линейная (закон Гука). При изучении изгиба следует обратить внимание на неравномерность распределения нормальных напряжений в поперечном сечении балки. На одной части сечения напряжения растягивающие, а на другой - сжимающие. В осевом сечении напряжения отсутствуют, и оно называется нейтральным слоем. Нормальные напряжения изменяются по высоте поперечного сечения пропорционально расстоянию от нейтральной оси. Следует уметь определять напряжения изгиба, которые зависят от действующего изгибающего момента М и момента сопротивления сечения при изгибе W. Условие прочности при изгибе 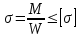 . .Значение величины Wзависит от размеров и формы поперечного сечения. Наличие поперечной силы, действующей на балку, связано с возникновением касательных напряжений в поперечных сечениях, а по закону парности касательных напряжений - в продольных сечениях. Касательные напряжения определяют по формуле Журавского. Поперечная сила сдвигает рассматриваемое сечение относительно смежного. Изгибающий момент, складывающийся из элементарных нормальных усилий, возникающих в поперечном сечении балки, поворачивает сечение относительно смежного, чем и обусловлено искривление оси балки, т. е. ее изгиб. Когда балка испытывает чистый изгиб, то по всей длине балки или на отдельном ее участке в каждом сечении действует постоянный изгибающий момент, а поперечная сила в любом сечении данного участка равна нулю. При этом в поперечных сечениях балки возникают только нормальные напряжения. Для того чтобы глубже разобраться в физических явлениях изгиба и в методике решения задач при расчете на прочность и жесткость, необходимо хорошо усвоить геометрические характеристики плоских сечений, а именно: статические моменты сечений, моменты инерции сечений как простой, так и сложной формы; научиться определять центры тяжести фигур сечений; главные моменты инерции сечений и главные оси инерции; центробежный момент инерции; изменение моментов инерции при повороте осей; усвоить теоремы о переносе осей. При изучении этого раздела следует научиться правильно строить эпюры изгибающих моментов и поперечных сил, определять опасные сечения и действующие в них напряжения. Помимо определения напряжений следует научиться определять перемещения точек нейтральной оси балки (прогибы балки) при изгибе. Для этого используется дифференциальное уравнение изогнутой оси балки (упругой линии), записанное в общем виде. Для определения прогибов проводится интегрирование уравнения упругой линии. При этом следует правильно определять постоянные интегрирования, исходя из условий опирания балки (граничных условий). Зная их, можно определить угол поворота и прогиб любого сечения балки. Изучение сложного сопротивления обычно начинают с косого изгиба. Явление косого изгиба особенно опасно для сечений со значительно отличающимися друг от друга главными моментами инерции: балки с таким сечением хорошо работают на изгиб в плоскости наибольшей жесткости, но даже при небольших углах наклона плоскости внешних сил к плоскости наибольшей жесткости в балках возникают значительные дополнительные напряжения и деформации. При определении напряжений в случае внецентренного растяжения или сжатия необходимо знать положение главных центральных осей сечения; именно от этих осей отсчитывают расстояния точки приложения силы и точки, в которой определяют напряжения. Приложенная эксцентрично сжимающая сила может вызвать в поперечном сечении стержня растягивающие напряжения. В связи с этим внецентренное сжатие является особенно опасным для стержней из хрупких материалов (кирпича, бетона), которые слабо сопротивляются растягивающим усилиям. В заключение следует изучить случай комбинированного нагружения, когда тело испытывает одновременно несколько видов деформаций: например, изгиб совместно с кручением, растяжение-сжатие совместно с изгибом и т. д. При этом следует иметь в виду, что изгибающие моменты, действующие в различных плоскостях, могут складываться как векторы. Вопросы для самопроверки 1. Какой изгиб называют чистым, а какой - поперечным? 2. Какие балки называют статически определимыми? 3. Как определить изгибающий момент и поперечную силу в каком-либо сечении балки? 4. Как формулируются правила знаков при определении величин изгибающих моментов и поперечных сил? 5. Какие допущения принимаются при изгибе? 6. Какая зависимость имеется между моментом и перерезывающей силой? 7. Как определить максимальный изгибающий момент? 8. Как распределены нормальные напряжения в поперечных сечениях балки? 9. Чему равны напряжения изгиба? 10. Что называется нейтральным слоем и где он расположен? 11. Что называется моментом инерции при изгибе? 12. В каких плоскостях возникают касательные напряжения при изгибе? 13. По какой формуле определяют величину касательных напряжений? 14. Как определить координаты центра тяжести плоской фигуры? 15. Чему равна сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей? 16. Какие оси называют главными? 17. Для каких фигур можно без вычислений определить положение главных центральных осей? 18. Относительно каких центральных осей осевые моменты инерции имеют наибольшее и наименьшее значения? 19. Что называют моментом сопротивления при изгибе? 20. Как выгоднее нагрузить балку прямоугольного сечения? 21. Как запишется дифференциальное уравнение изогнутой оси балки в общем виде? 22. Как найти постоянные интегрирования и что они обозначают? 23. Как найти наибольшее значение прогиба? 24. Какой случай изгиба называют косым изгибом? 25. В каких точках поперечного сечения, возникают наибольшие напряжения при косом изгибе? 26. Как находят положение нейтральной линии при косом изгибе? 27. Как пройдет нейтральная линия, если плоскость действия сил совпадает с диагональной плоскостью балки прямоугольного поперечного сечения? 28. Как определяют деформации при косом изгибе? 29. Чему равно напряжение в центре тяжести поперечного сечения при внецентренном растяжении или сжатии? 30. Как находят напряжения в произвольной точке поперечного сечения при внецентренном растяжении или сжатии? 31. Чему равно напряжение в центре тяжести поперечного сечения при внецентренном растяжении или сжатии? 32. Какое положение занимает нейтральная линия, когда продольная сила приложена в вершине ядра сечения? 33. Какие напряжения возникают в поперечном сечении стержня при изгибе с кручением? 34. Как находят опасные сечения стержня при изгибе с кручением? 35. В каких точках круглого поперечного сечения возникают наибольшие напряжения при изгибе с кручением? 36. Как находится числовое значение расчетного момента при изгибе с кручением стержня круглого поперечного сечения? 3. Сдвиг и кручение Сдвигом называют такой вид напряженного состояния, когда на гранях элемента действуют только касательные напряжения. Деформации, возникающие при сдвиге, называют угловыми деформациями или углом сдвига. Опыты показывают, что между напряжениями и деформациями при сдвиге существует линейная зависимость, аналогичная закону Гука при растяжении. Закон Гука при сдвиге имеет вид 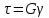 , ,где γ- угол сдвига; G - модуль упругости второго рода, или модуль сдвига. Следует обратить внимание на то, что модуль продольной упругости Е и модуль упругости при сдвиге Gдля одного и того же материала связаны через коэффициент Пуассона µ зависимостью 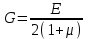 . .При расчетах на срез обычно принимают, что касательные напряжения распределены равномерно в поперечном сечении стержня и условие прочности на срез имеет вид 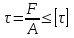 . .Допускаемые напряжения [τ] на сдвиг (срез) составляют некоторую часть от допускаемых напряжений на растяжение. Рассчитывают на срез соединения заклепочные, болтовые, сварные, шпоночные и некоторые другие типы соединений. При проведении прочностных расчетов на сдвиг (срез) необходимо научиться правильно определять площади среза для односрезных и многосрезных заклепок, а также для углового сварного шва, в котором срез происходит по биссекторной плоскости прямого угла поперечного сечения шва. Если в поперечном сечении стержня действует крутящий момент Т, то стержень испытывает кручение. Необходимо, используя метод сечений, научиться строить эпюры крутящих моментов по длине стержня и определять возникающие при этом касательные напряжения, определяемые из соотношения 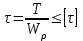 , ,где Wρ- полярный момент сопротивления сечения кручению. В поперечном сечении бруса касательные напряжения распределены неравномерно. Так для стержня с круглым поперечным сечением касательные напряжения изменяются по линейному закону - от нуля на центральной оси до максимального значения у поверхности. Так как сечения, расположенные у оси стержня, нагружены незначительно, то с целью экономии материала при кручении целесообразно использовать пустотелые профили. Крутящий момент в сечении скручиваемого стержня (вала) численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения. Если на брус круглого поперечного сечения действуют одновременно крутящий и изгибающий моменты, то расчет на прочность таких брусьев (валов) производится с использованием третьей или четвертой гипотез прочности. Вопросы для самопроверки 1. Что называется абсолютным и относительным сдвигом? 2. Что называется законом парности касательных напряжений при сдвиге? 3. Как формулируется закон Гука при сдвиге? 4. Как связаны между собой модуль продольной упругости Е и модуль сдвига G? 5. Как производится расчет на прочность при сдвиге (срезе)? 6. Как распределены напряжения в поперечном сечении при сдвиге? 7. Как рассчитывают на срез заклепочные и сварные соединения? 8. Что называют кручением? 9. Какие напряжения возникают в поперечном сечении круглого стержня при кручении? 10. Как определить величину напряжений при кручении? 11. Как определить допустимые напряжения при кручении? 12. Как определить полярный момент инерции и полярный момент сопротивления сечения при кручении? Какова их размерность? 13. Как определить угол закручивания стержня? 14. Как записать условие прочности при кручении? 15. В чем заключается расчет вала на жесткость? 16. Как рассчитывают валы на сложное сопротивление (изгиб совместно с кручением)? 4. Напряженное и деформированное состояние в точке Совокупность нормальных и касательных напряжений, действующих по различным площадкам, проходящим через рассматриваемую точку, называют напряженным состоянием в точке. Необходимо уяснить характер изменения нормальных и касательных напряжений в наклонных сечениях в зависимости от угла наклона при линейном (одноосном) и плоском (двухосном) напряженном состоянии и понятия о главных напряжениях. Пространственный (трехосный) случай напряженного состояния - общий случай напряженного состояния, при котором относительные деформации определяют на основании обобщенного закона Гука. В теории упругости доказывается, что при пространственном напряженном состоянии через каждую точку всегда можно провести три площадки, по которым касательные напряжения равны нулю. Такие площадки называют главными, а нормальные напряжения, действующие под ним, - главными напряжениями σ1, σ2, σ3. Все три главные площадки взаимно перпендикулярны. Сумма нормальных напряжений, действующих по любым трем взаимно перпендикулярным площадкам, проходящим через рассматриваемую точку, есть величина постоянная. Принято следующее обозначение соотношений между главными напряжениями: σ1>σ2>σ3. При таком напряженном состоянии сумма нормальных напряжений по двум взаимно перпендикулярным площадкам есть величина постоянная и равная сумме главных напряжений. Касательные напряжения по двум взаимно перпендикулярным площадкам равны по величине и противоположны по знаку. Это свойство обычно называют «законом парности касательных напряжений». Наибольшие касательные напряжения равны полуразности главных напряжений и действуют по площадкам, наклоненным к главным площадкам на угол 45° и перпендикулярным плоскости чертежа. Предельное напряженное состояние в общем случае зависит от соотношения между тремя главными напряжениями. Поэтому в случае сложного напряженного состояния следует найти эквивалентное напряжение, при котором возникает опасность разрушения, и сравнить его с допустимым, полученным при опыте на растяжение - сжатие. Таким образом задача теорий (гипотез) прочности состоит в оценке возможности разрушения материала при сложном напряженном состоянии на основании характеристик материала, полученных при простом растяжении - сжатии. При рассмотрении гипотез предельных состояний (гипотез прочности) надо иметь в виду, что они основываются на предпосылке, что два каких-либо напряженных состояния считаются равноопасными, если они при увеличении главных напряжений в одно и то же число раз одновременно становятся предельными. В этом случае коэффициент запаса прочности для обоих напряженных состояний в указанных условиях будет одинаковым. Гипотез прочности существует несколько, так как одни дают удовлетворительные результаты для хрупких материалов, а другие - для пластичных. Первая гипотеза прочности - гипотеза наибольших нормальных напряжений, вторая гипотеза прочности - гипотеза наибольших линейных деформаций, третья - гипотеза наибольших касательных напряжений и четвертая - энергетическая гипотеза прочности. Вопросы для самопроверки 1. Что называют напряженным состоянием в точке? 2. Какие виды напряженного состояния встречаются? 3. Какие площадки называют главными? 4. Какие напряжения называют главными? 5. Чему равна сумма нормальных напряжений по двум взаимно перпендикулярным площадкам? 6. Сущность закона парности касательных напряжений. 7. Чему равны наибольшие касательные напряжения и где они действуют? 8. Что называется обобщенным законом Гука? 9. В чем задача теорий прочности? 10. Какие теории прочности существуют? 11. Как в случае плоского напряженного состояния найти эквивалентные напряжения по третьей и четвертой теориям прочности? 12. Почему существуют несколько теорий прочности? 13. Чему равна удельная работа деформаций при объемном напряженном состоянии? 5. Устойчивость сжатых тонкостенных конструкций При изучении этого раздела следует обратить внимание на такие понятия, как устойчивость стержня (системы), потеря устойчивости, значение критической силы, критические напряжения. При потере устойчивости значение критических напряжений может быть меньше предела текучести материала. Критическая сила определяется по формуле Эйлера для стержней большой гибкости и по формуле Ясинского для стержней малой и средней гибкости. Она зависит от жесткости стержня, его длины и условий закрепления концов стержня, учитываемых коэффициентом приведения длины µ. Допускаемые напряжения на устойчивость составляют некоторую часть от допускаемых напряжений при расчетах на прочность 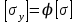 , ,где φ - коэффициент уменьшения допускаемого напряжения для сжатых стержней (его значения приведены в справочниках). Коэффициент φ зависит от гибкости и материала стержня: его использование позволяет производить расчеты на продольный изгиб так же, как для случая простого сжатия. При подборе размеров поперечного сечения стержня используется метод последовательных приближений. При проведении расчетов необходимо уметь определять коэффициент запаса устойчивости. Вопросы для самопроверки 1. Какая система называется устойчивой? 2. В чем заключается явление потери устойчивости сжатого стержня? 3. Что называют критической силой? 4. По какой формуле следует определять критическую силу для стержней большой гибкости? 5. Для каких стержней применима формула Ясинского? 6. Какие параметры влияют на величину критической силы? 7. Что называется гибкостью стержня? 8. Для каких значений гибкости стержня применима формула Эйлера? 9. Как учитывается влияние способа закрепления концов стержня? 10. Что такое коэффициент φ и от чего зависит его числовое значение? 11. Как производится проверка стержней на устойчивость? 12. Как проводится выбор типа сечения для обеспечения устойчивости сжатого стержня? 6. Концентрация напряжений в элементах конструкций Равномерное распределение напряжений нарушается там, где в детали имеются разного рода концентраторы напряжений в виде отверстий, выточек, резкого перехода от сечений одних размеров и форм к другим, какие-либо внутренние или внешние повреждения, неоднородность строения материала и т. п. В этих местах напряжения могут резко изменяться. Эта особенность в распределении напряжения называется концентрацией, а сами напряжения - местными или локальными (ввиду ограниченности области их действия). При статическом нагружении основным показателем местных напряжений является теоретический коэффициент концентрации, выведенный для таких концентраторов, как отверстие, выточка, галтель и т. д., а также свойства самого материала, что наиболее важно при переменных напряжениях. Поэтому вводится понятие эффективного коэффициента концентрации напряжений; который определяют по графикам или таблицам, приводимым в справочной литературе. К контактным относятся напряжения, возникающие в зоне контакта двух тел. Различают точечный и линейный контакты. При этом контактные напряжения распределены по площади контакта неравномерно, а наибольшие напряжения определяют по формуле Герца. Контактные напряжения определяют при расчетах, например, зубчатых и фрикционных передач. Вопросы для самопроверки 1. Что такое концентратор напряжения? 2. Какие напряжения называют местными и как их определяют? 3. Что называют теоретическим коэффициентом концентрации напряжений? 4. Что называют эффективным коэффициентом концентрации напряжений? 5. Какие напряжения называют контактными и как определить их величину? 7. Понятие об усталости материала Элементы машин и конструкций часто работают при периодически изменяющихся (циклических) нагрузках. Разрушение конструкций происходит из-за образования и развития микротрещин. Следует обратить внимание на построение кривой усталости для материалов при действии переменных напряжений, уметь определять предел выносливости, усвоить методы повышения сопротивления усталости при проектировании деталей машин и конструкций и определение запаса прочности при циклическом нагружении элементов конструкций. Вопросы для самопроверки 1. Что называют пределом выносливости материала? 2. Как предел выносливости связан с пределом прочности? 3. Как строится кривая усталости материала? 4. Что называют коэффициентом асимметрии цикла? 5. Что влияет на предел выносливости? 6. Какие мероприятия проводятся для повышения сопротивления усталости проектируемых деталей? 7. В чем заключается расчет деталей на сопротивление усталости? |
