Метод. указания по практическим занятиям Прим ЭВМ в ТР ИЗО-2018. Методические указания к практическим занятиям по дисциплине Применение электронновычислительных машин в тепловых расчетах Практическое занятие
 Скачать 323.57 Kb. Скачать 323.57 Kb.
|
|
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №2 «Численное решение одномерных задач нестационарной теплопроводности методом конечных разностей по явной и неявной схемам» Цель работы: приобретение навыков расчета одномерных задач нестационарной теплопроводности методом конечных разностей по явной и неявной схемам. На практике часто можно встречаются случаи, когда изменение температуры происходит только по одной координате (направлению) и по времени. Например, охлаждение или нагревание плоской неограниченной пластины; стержня, заизолированного с боковой поверхности и др. Одним из наиболее простых методов решения таких одномерных задач нестационарной теплопроводности является метод конечных разностей, реализуемый по, так называемой, явной или неявной схеме. Постановка задачи Найти температурное поле в теплоизолированном с боковой поверхности ограниченном стержне длиной L (см.рис.4), разделенным на 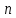 частей, при следующих краевых условиях: частей, при следующих краевых условиях:- начальные условия: в начальный момент времени температура тела являлась функцией координат и задана во внутренних точках-узлах (i=1,2,…,n-1), то есть при 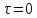 , ,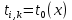 ; ;- граничные условия: на левой и правой границах стержня задана и постоянна во времени температура, то есть при 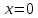 , , 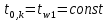 ; ;при 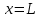 , , 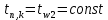 . .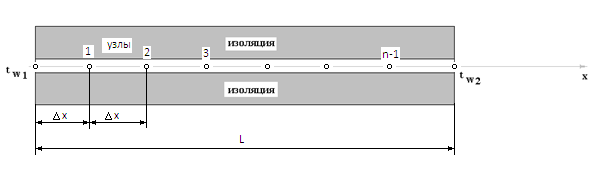 Рис.4. Теплоизолированный с боковой поверхности стержень Примечание: шаг по времени рассчитать по формуле: 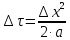 , где , где 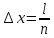 – шаг по координате. – шаг по координате.Числовые значения исходных данных взять из таблицы вариантов (табл.2). Таблица 2
Изложение численного метода Дифференциальное уравнение нестационарной теплопроводности в случае одномерной задачи имеет вид 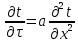 . (1) . (1)Для численного решения этого уравнения воспользуемся методом конечных разностей или методом сеток. В соответствии с этим методом на пространственно-временную область АВСD одномерной задачи (см.рис.5) наносится сеточная область с шагом сетки по оси х - 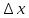 и по времени τ - и по времени τ - 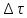 . . Рис.5. Пространственно-временная область одномерной задачи теплопроводности Затем уравнение (1) заменяют конечно-разностной аппроксимацией (приближением). Конечно-разностное уравнение (1) может быть сделано по различным схемам. Для уравнения теплопроводности различают два типа разностных схем: явную и неявную. Явную схему мы получим, если возьмем разностное представление производной по времени в (1) «вперед» 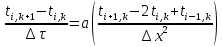 (2) (2)(Здесь выражение для второй производной по координате представлено конечно-разностной аппроксимацией 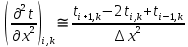 аналогично тому, что показано в практическом занятии №1). аналогично тому, что показано в практическом занятии №1).Отсюда 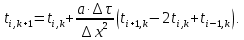 (3) (3)В частности, при 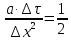 (4) (4)формула (3) приобретает особенно простой вид 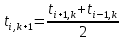 , (5) , (5)то есть температура в данном узле для момента времени k+1 равна среднеарифметическому значений температур в соседних узлах для момента времени k. Из формул (3) и (5) видно, что температура для последующего момента времениk+1 явным образом выражается через температуры для предыдущего момента времениk, поэтому схема и называется явной. Таким образом, начиная с какого-то начального момента времени k, можно последовательно вычислить все температуры для моментов k+1, k+2, k+3,…,k+n. Исследования показали, что данная схема будет устойчивой, то есть ошибки неточного задания краевых условий и неизбежные промежуточные округления при расчетах не будут возрастать при увеличении шага по времени 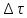 , если выполняется условие , если выполняется условие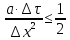 , (6) , (6)откуда 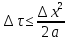 . (7) . (7)Последнее условие весьма обременительно. Как показывают практические расчеты, при достаточно малых шагах по координате 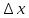 и конкретных значениях коэффициента температуропроводности а величина и конкретных значениях коэффициента температуропроводности а величина 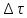 оказывается очень малой и приходится делать большое число шагов по времени τ. Все это повышает трудоемкость решения. оказывается очень малой и приходится делать большое число шагов по времени τ. Все это повышает трудоемкость решения.Таким образом, условие (7) ограничивает использование явной схемы метода конечных разностей для расчета одномерного нестационарного температурного поля. Рассмотрим теперь метод конечных разностей, реализуемый по неявной схеме, когда температуры для последующего момента времени выражаются через одну известную температуру предыдущего момента времени. Неявные разностные уравнения решаются сложнее, чем явные, но они абсолютно устойчивы при любом шаге по времени. Это позволяет выбирать шаг ∆τ значительно большим, чем в явных схемах, и соответственно уменьшать общее время счета всей задачи. Итак, если взять приближенное значение производной по времени «назад» (см.рис.5), то получим следующее конечно-разностное соотношение: 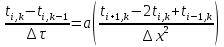 . (8) . (8)Это уравнение решается труднее, поскольку в него входят три неизвестные температуры: 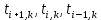 . Поэтому в данном случае нужно решать сразу всю систему разностных уравнений типа (8) - систему линейных алгебраических уравнений (СЛАУ) для всех точек-узлов i,k сетки. . Поэтому в данном случае нужно решать сразу всю систему разностных уравнений типа (8) - систему линейных алгебраических уравнений (СЛАУ) для всех точек-узлов i,k сетки. Методы решения СЛАУ хорошо известны. В данной работе предлагается воспользоваться онлайн-калькулятором сети Интернет, которых на просторах всемирной паутины большое количество (например, matrixcalc.org). Чтобы использовать онлайн-калькулятор нужно записать для каждой внутренней точки-узла (i=1, 2, 3 …n-1) уравнение (8) и преобразовать его так, чтобы иметь возможность вносить коэффициенты в ячейки системы уравнений (см. пример выполнения отчета - Приложении 3). Также для нашего случая можно применить другой численный метод решения одномерной нестационарной задачи теплопроводности - метод прогонки. Изложим метод прогонки на примере. Уравнение (8) можно также записать через моменты времени k+1 и k 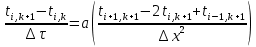 . (9) . (9)По условию нашей задачи начальные и граничные условия будут следующие: в момент времени k=0 температура тела являлась функцией координат и задана во внутренних точках-узлах (i=1,2,…,n-1) 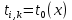 , (10) , (10)а на левой и правой границе температура поддерживается постоянной (ГУ-1 рода) 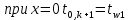 , (11) , (11)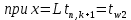 . (12) . (12)Уравнение (9) для удобства дальнейших выводов запишем в виде 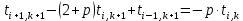 , (13) , (13)где 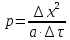 . . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
