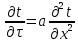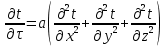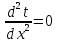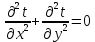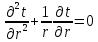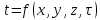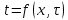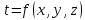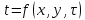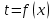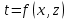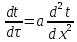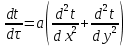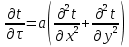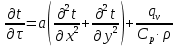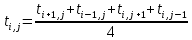Метод. указания по практическим занятиям Прим ЭВМ в ТР ИЗО-2018. Методические указания к практическим занятиям по дисциплине Применение электронновычислительных машин в тепловых расчетах Практическое занятие

• Название: Методические указания к практическим занятиям по дисциплине Применение электронновычислительных машин в тепловых расчетах Практическое занятие
• Дата: 16.09.2022
• Размер: 323.57 Kb.
• Имя файла: Метод. указания по практическим занятиям Прим ЭВМ в ТР ИЗО-2018 .docx
• Тип: Методические указания; #680692
• страница: 2 из 6

КОНТРОЛЬНЫЕ ВОПРОСЫ – ТЕСТ по практическому занятию №1
Укажите в правом столбце правильный ответ!

1)

При стационарной теплопроводности….
температура в любой точке тела не зависит и не меняется с течением времени
коэффициент теплопроводности не меняется у тела с течением времени
температура в любой точке тела меняется с течением времени

2)

Метод конечных разностей принадлежит к …
Аналитическим методам решения задач теплопроводности
Точным аналитическим методам решения задач теплопроводности
Численным методам решения задач теплопроводности
Приближенным аналитическим методам решения задач теплопроводности

3)

Основная идея метода конечных разностей заключается в том, чтобы
Заменить дифференциальное уравнение теплопроводности на дифференциальное уравнение с обыкновенными производными
Заменить уравнение Лапласа на дифференциальное уравнение с обыкновенными производными
Преобразовать систему алгебраических уравнений в конечные разности
Перевести дифференциальное уравнение в частных производных в алгебраические уравнения с заменой дифференциалов на конечные разности.

4)

Понятие «итерация» - это по-другому?
Аппроксимация
Приближение к верному решению, новый пересчет
Замена одного другим
Сходимость данного метода

5)

Температурное поле двухмерной области без внутренних источников теплоты описывается уравнением…

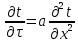
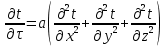
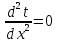
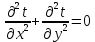
6)

Одномерное плоское стационарное температурное поле описывается уравнением

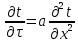
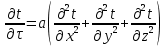
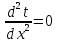
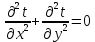
7)

Одномерное цилиндрическое температурное поле описывается уравнением

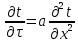
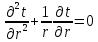
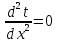
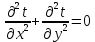
8)

Укажите математическое выражение 3-мерного стационарного температурного поля

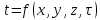
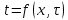
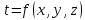
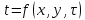
9)

Укажите математическое выражение одномерного нестационарного температурного поля

10)

Метод сеток – это, по-другому, метод конечных разностей?
Да
Нет

11)

Укажите математическое выражение 1-мерного стационарного температурного поля

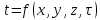
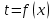
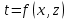
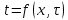
12)

Как называется коэффициент «а» в дифференциальном уравнении ?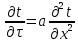
Это коэффициент теплоотдачи
Это коэффициент теплопроводности
Это коэффициент температуропроводности

13)

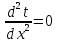Это уравнение в обыкновенных производных?
Да
Нет

14)

Уравнение 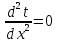можно уже интегрировать?
Да
Нет

15)

Продолжите предложение: «Процесс итераций считается законченным тогда, когда
достигнуто нулевое приближение
в пределах заранее заданной точности система значений искомой функции № (n+1) совпадает с системой № n.
расчет температуры в некоторых узлах уже приводит к повторению значений по температуре

16)

Можно ли не учитывать в методе итераций граничные условия на поверхности тела?
Да
Нет

17)

Можно ли процесс итераций считать завершенным, если во всех узлах области погрешность в определении температуры становится меньше, чем заранее заданное значение погрешности вычислений?
Да
Нет

18)

Метод Гаусса – это метод решения системы линейных алгебраических уравнений?
Да
Нет

19)

Какое из приведенных уравнений записано неверно?

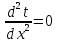
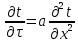
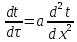
20)

Какое из приведенных уравнений записано неверно?

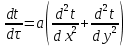
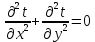
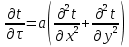
21)

Какое из дифференциальных уравнений учитывает наличие в теле внутренних источников теплоты?

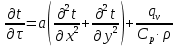
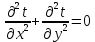
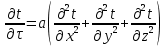
22)

Математическая постановка двумерной задачи стационарной теплопроводности включает в себя
Дифференциальное уравнение теплопроводности Граничные условия на поверхности тела
Дифференциальное уравнение теплопроводности Начальное условие Граничные условия на поверхности тела
Начальные условия Граничные условия на поверхности тела Геометрические условия

23)

Укажите, верно ли утверждение, что расчет по методу итераций для двумерной области обязательно нужно начинать с крайнего левого узла?
Нет. Расчет можно начинать с любого узла сеточной области
Да. Нужно начинать с левого крайнего, т.к. там уже заданы точно две граничные температуры

24)

Вставьте пропущенное слово: «При расчете двумерной области стационарной теплопроводности для уточнения значений температур в узлах сетки необходимо находить среднеарифметическое значение…соседних узлов?»
двух
трех
четырех
восьми

25)

Укажите решение данного уравнения по методу конечных разностей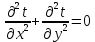

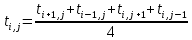
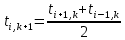
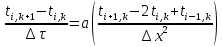
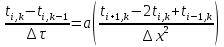
26)

Как определяется погрешность расчета после трех итераций?
Нужно результаты третьей итерации сравнить с результатами второй итерации
Нужно результаты третьей итерации сравнить с результатами первой итерации
Нужно результаты третьей итерации сравнить с первоначально заданными значениями в узлах сетки

27)

Что понимается под двумерной задачей теплопроводности?
Изменение температурного поля идет по двум направлениям, например x и y.
Изменение температурного поля идет по координате и времени
Под двумерной задачей понимается задача теплопроводности с двумя граничными условиями

28)

Можно ли применить метод конечных разностей для решения двумерной задачи стационарной теплопроводности без использования метода итераций?
Да, необходимо для всех узлов сеточной области составить конечно-разностные уравнения связи и решить ее методами СЛАУ.
Нет, только метод итераций позволяет определить значения температур в этом случае

29)

Количество итераций влияет на точность конечного результата?
Да, увеличение числа итераций улучшает точность расчетов
Нет, увеличение числа итераций может привести к ухудшению точности вычислений, вследствие накопления ошибок при округлении

30)

Если в теле присутствуют внутренние источники теплоты, то задача теплопроводности становится нелинейной?
Нет
Да