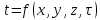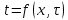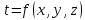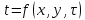Метод. указания по практическим занятиям Прим ЭВМ в ТР ИЗО-2018. Методические указания к практическим занятиям по дисциплине Применение электронновычислительных машин в тепловых расчетах Практическое занятие
 Скачать 323.57 Kb. Скачать 323.57 Kb.
|
|
Отчет по практическому занятию №1 «Применение метода конечных разностей в двумерных задачах стационарной теплопроводности» Цель работы - приобретение навыков расчета двумерных задач стационарной теплопроводности методом конечных разностей (методом сеток) и методом итераций. Постановка задачи Найти температурное поле в углу печи (здания) (рис.3), если на поверхностях DС и DЕ задана температура tw2, на поверхностях АВ и АF – температура tw1. На поверхностях ВС и FE имеют место линейные законы распределения температуры. Расчет на ЭВМ производить с точностью δt. Дать графическое представление результатов ручного расчета и расчета на ЭВМ в виде двумерного температурного поля с изображением на нем трех изотерм (t17, t26, t35). Сделать выводы по проделанной работе. Ответить на контрольные вопросы – тест по практическому занятию. 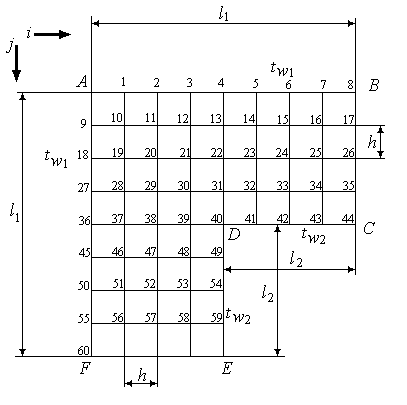 Рис.1. Сеточная область угла здания Числовые значения температуры и размеров области из табл.1. Таблица 1
Расчет температурного поля методом итераций (ручной счет двух итераций) с необходимыми пояснениями. Рассчитаем сначала температуры на боковых поверхностях ВС и FE, где по условию заданы линейные законы распределения температур. Так как сторона ВС разделена на 4 части, то для определения температуры в узле 17, нужно 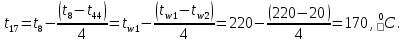 В середине стороны ВС, т.е. в узле 26, температуру можно найти 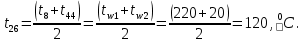 В узле 35 температура определится так 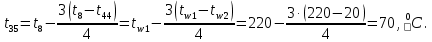 На стороне FE, вследствие симметрии, температуры будут равны 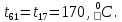 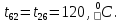 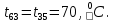 1 ИТЕРАЦИЯ Согласно уравнению (5) температура в любом внутреннем узле области находится как среднеарифметическое значение четырех соседних узлов. Для начала расчетов примем значения температуры во внутренней области как среднее между tw1 и tw2 , т.е. 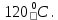 Расчет начнем с 10 внутреннего узла, т.к. там точно заданы две граничные температуры. Расчет начнем с 10 внутреннего узла, т.к. там точно заданы две граничные температуры.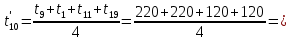 170 170  Температуру в 11 внутреннем узле будем искать, используя уже найденную (уточненную) температуру в 10 узле. 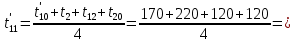 157,5 157,5  Аналогичным образом проведем расчет других внутренних узлов 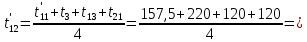 154,4 154,4  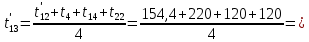 153,6 153,6  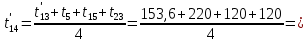 153,4 153,4 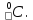 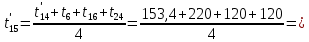 153,35 153,35 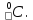 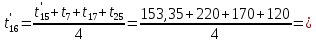 165,8 165,8 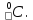 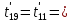 157,5 157,5 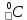 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.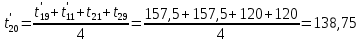 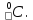 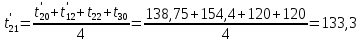 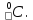 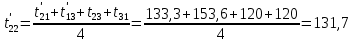 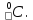 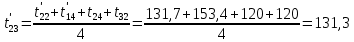 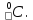 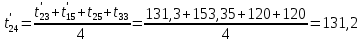 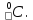 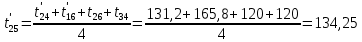 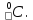 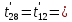 154,4 154,4 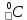 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.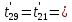 133,3 133,3 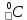 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.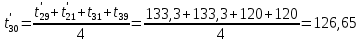 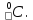 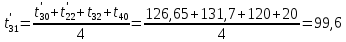 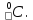 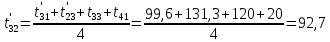  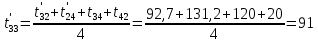  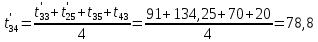 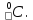 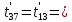 153,6 153,6 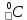 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.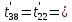 131,7 131,7 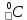 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.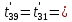 99,6 99,6 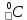 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.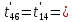 153,4 153,4 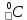 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.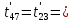 131,3 131,3 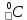 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.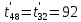 ,7 ,7 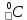 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.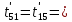 153,35 153,35 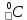 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.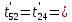 131,2 131,2 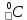 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.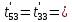 91 91 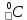 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.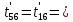 165,8 165,8 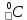 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.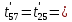 134,25 134,25 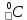 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.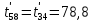 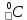 - вследствие геометрической симметрии тела и граничных условий. - вследствие геометрической симметрии тела и граничных условий.2 ИТЕРАЦИЯ При повторном вычислении будем использовать значения температуры во внутренних узлах из первой итерации. 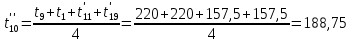 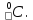 Аналогичным образом рассчитаем температуры и в других внутренних узлах 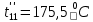 ; ; 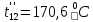 ; ; 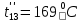 ; ; 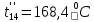 ; ; 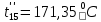 ; ; 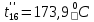 ; ; 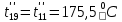 ; ; 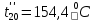 ; ; 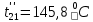 ; ; 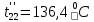 ; ; 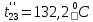 ; ; 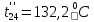 ; ; 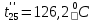 ; ; 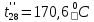 ; ; 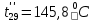 ; ; 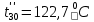 ; ; 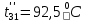 ; ; 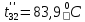 ; ; 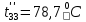 ; ; 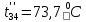 ; ; 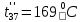 ; ; 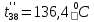 ; ; 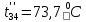 ; ; 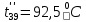 ; ; 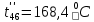 ; ; 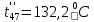 ; ; 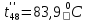 ; ; 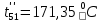 ; ; 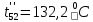 ; ; 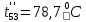 ; ; 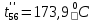 ; ; 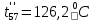 ; ; 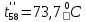 . .Расчет температурного поля на ЭВМ. 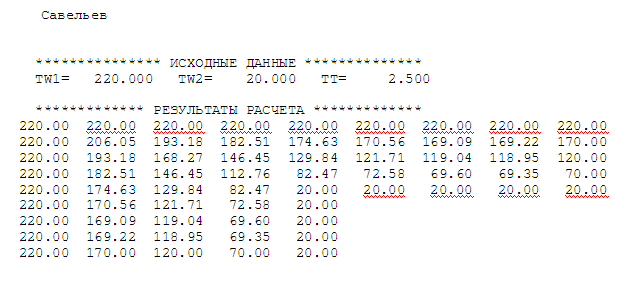 Графическое представление результатов расчета. По результатам расчета получили следующее температурное поле (рис.2а, 2б), в котором изобразили три изотермы ( 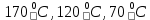 ). ).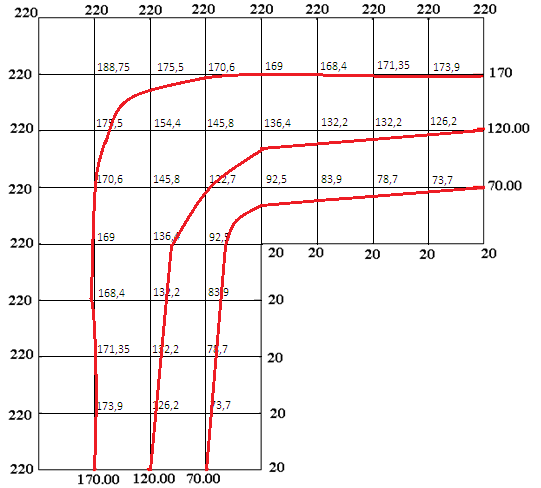 Рис.2а. Результаты ручного расчета после двух итераций 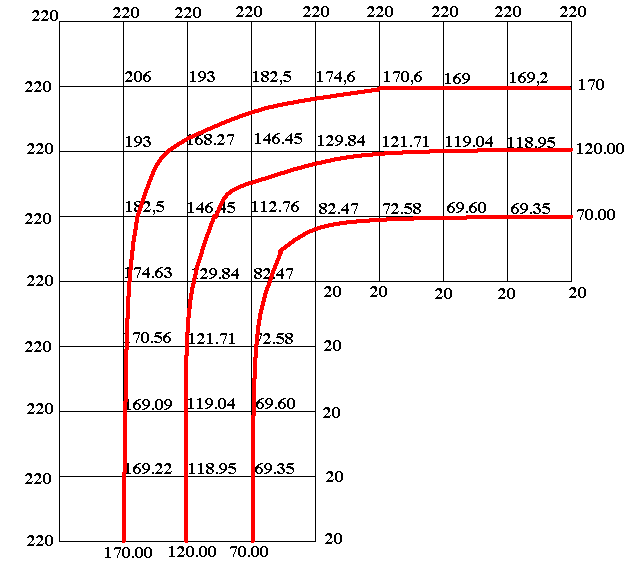 Рис.2б. Результаты расчета на ЭВМ до заданной точности Выводы по проделанной работе и полученным результатам расчета: - освоен алгоритм расчета двумерного стационарного температурного поля методом конечных разностей и методом итераций; - проведено сравнение результатов расчета после двух итераций и расчета на ЭВМ до заданной точности, которое позволило определить погрешность в определении истинных значений температуры в исследуемой области; - представлено наглядное изображение температурного поля с отмеченными на нем тремя изотермами; - даны ответы на контрольные вопросы – тест по практическому занятию. Ответы на контрольные вопросы – тест по практическому занятию 8)
18)
28)
Приложение 3 Отчет по практическому занятию №2 «Численное решение одномерных задач нестационарной теплопроводности методом конечных разностей по явной и неявной схемам» Цель работы: приобретение навыков расчета одномерных задач нестационарной теплопроводности методом конечных разностей по явной и неявной схемам. Постановка задачи Найти температурное поле в теплоизолированном с боковой поверхности ограниченном стержне длиной L (см.рис.4), разделенным на 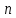 частей, при следующих краевых условиях: частей, при следующих краевых условиях:- начальные условия: в начальный момент времени температура тела являлась функцией координат и задана во внутренних точках-узлах (i=1,2,…,n-1), то есть при 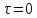 , ,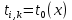 ; ;- граничные условия: на левой и правой границах стержня задана и постоянна во времени температура, то есть при 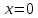 , , 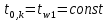 ; ;при 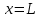 , , 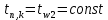 . .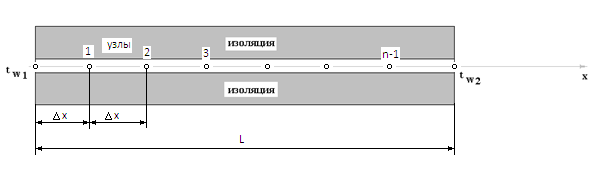 Рис.1. Теплоизолированный с боковой поверхности стержень Примечание: шаг по времени рассчитать по формуле: 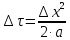 , где , где 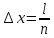 – шаг по координате. – шаг по координате.Числовые значения исходных данных взять из таблицы вариантов (табл.2). Таблица 2
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||