Метод. указания по практическим занятиям Прим ЭВМ в ТР ИЗО-2018. Методические указания к практическим занятиям по дисциплине Применение электронновычислительных машин в тепловых расчетах Практическое занятие
 Скачать 323.57 Kb.
|
|
Расчет температурного поля для трех моментов времени с необходимыми пояснениями по явной схеме. Согласно формуле (5) температура в узле для момента времени k+1 равна среднеарифметическому из значений температур в соседних узлах для момента времени k. Значит, в узле 1 для следующего (после начального) момента времени (к=1) температура определится как 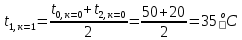 .Рассчитывая аналогично для других внутренних узлов, получим распределение температуры в стержне для момента времени k=1, учитывая, что условия на границе тела заданы и не изменяются. Далее используя распределение температур для момента времени k=1, определим также по формуле (5) распределение температур для момента времени k=2 и k=3. Результаты расчетов представлены на рис.2. 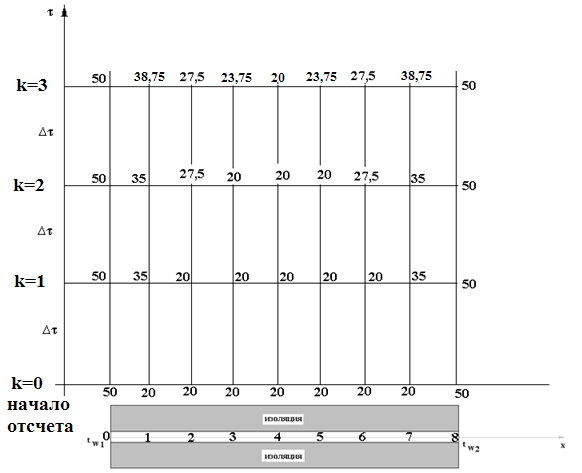 Рис.2. Результаты расчетов для трех шагов по времени Результаты расчета температурного поля на ЭВМ Для внесения необходимых данных в программу для расчета температур стержня определим следующие величины: - примем разбивку стержня на восемь частей (согласно своего варианта), то есть 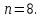 - коэффициент температуропроводности 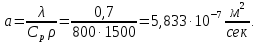 - шаг по координате 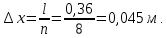 - максимальный шаг по времени определим по формуле (7) 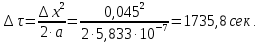 Необходимо выбрать шаг по времени меньше полученного, поэтому примем 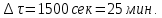 - количество шагов по времени выберем 10. (Количество шагов по времени в отчете достаточно указать всего три). 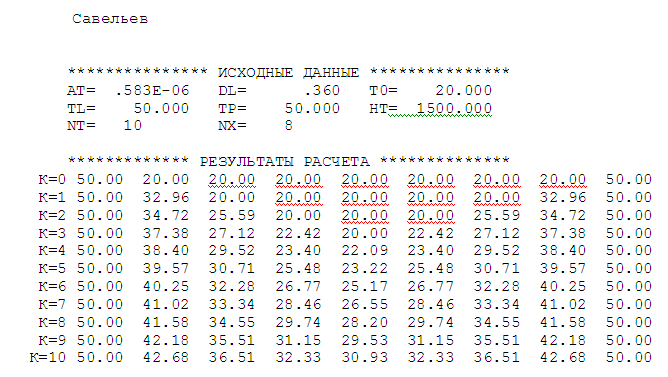 Построим график распределения температур в стержне для следующих моментов времени (к=1, к=3, к=5, к=7, к=9) 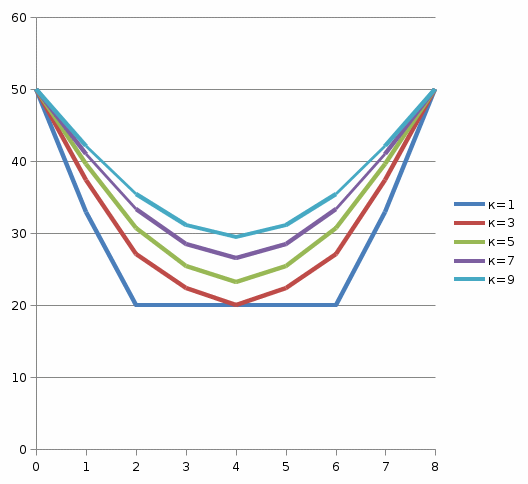 Рис.3. Распределение температур стержня в различные моменты времени Сравнивая результаты расчетов, приходим к выводу, что значения температур в узлах совпали. Расчет температурного поля для одного шага по времени методом прогонки Теперь решим ту же самую задачу другим методом – методом прогонки. Далее в качестве примера взяты следующие исходные данные:
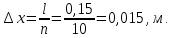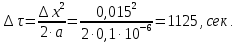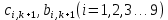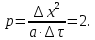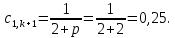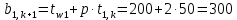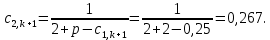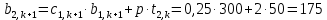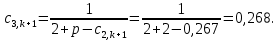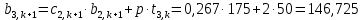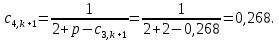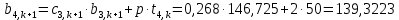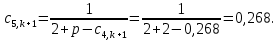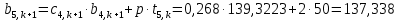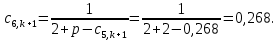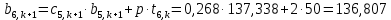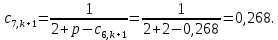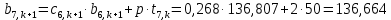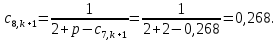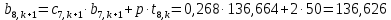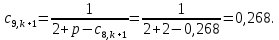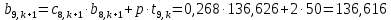Найдем сначала шаг по координате  Тогда шаг по времени будет  Пользуясь системами (А) и (В), производя «прогонку» слева-направо в прямом направлении, последовательно найдем все коэффициенты  , предварительно определив постоянную p.   .  .  .  .  .  .  .  .  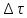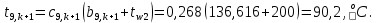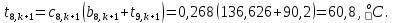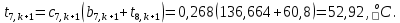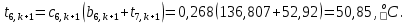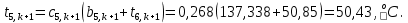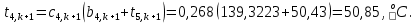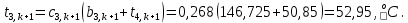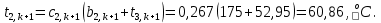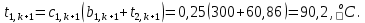.Теперь по формуле (9) определим температуры для следующего момента времени (через шаг  ), начиная расчет от правого внутреннего узла         Расчет температурного поля для одного шага по времени с помощью онлайн-калькулятора в сети Интернет Для того чтобы воспользоваться онлайн-калькулятором в сети Интернет, необходимо записать девять уравнений вида (8) для всех внутренних узлов. 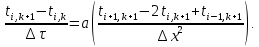 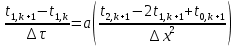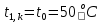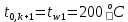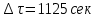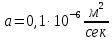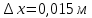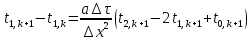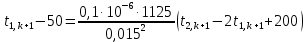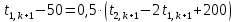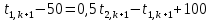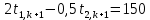Тогда для первого внутреннего узла (i=1) это уравнение примет вид  .Зная, что  ;  ;  ;  ;  , то после преобразований получим ; ; ; ; .Проводя аналогичные преобразования для всех последующих узлов, получим систему из 9 алгебраических линейных уравнений 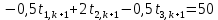 ; ;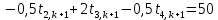 ; ;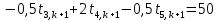 ; ;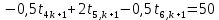 ; 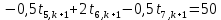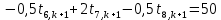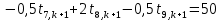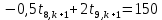.Воспользуемся онлайн-калькулятором (http://matrixcalc.org/slu.html), внесем туда свою систему коэффициентов  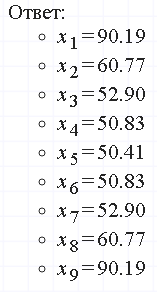 Сравнивая результаты расчетов, приходим к выводу, что значения температур в узлах совпали. Далее нужно ответить на контрольные вопросы – тест согласно своего варианта. |
