|
|
Метод. указания по практическим занятиям Прим ЭВМ в ТР ИЗО-2018. Методические указания к практическим занятиям по дисциплине Применение электронновычислительных машин в тепловых расчетах Практическое занятие
Идея метода прогонки заключается в следующем: представим связь между двумя температурами соседних узлов 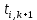 и и 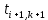 в виде в виде
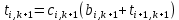 , (14) , (14)
где 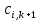 и и 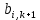 некоторые коэффициенты, подлежащие определению. Если они будут известны, то делая «прогонку» в направлении справа-налево, начиная с правого граничного условия некоторые коэффициенты, подлежащие определению. Если они будут известны, то делая «прогонку» в направлении справа-налево, начиная с правого граничного условия 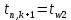 , можно по (14) последовательно найти все температуры в (k+1)-м слое по времени. Из (14), заменяя i на i-1, имеем , можно по (14) последовательно найти все температуры в (k+1)-м слое по времени. Из (14), заменяя i на i-1, имеем
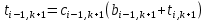 , (15) , (15)
Подставляя (15) в формулу (13), получим
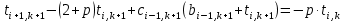 . (16) . (16)
Отсюда
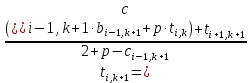 . (17) . (17)
Сравнивая (14) с (17), приходим к следующим соотношениям:
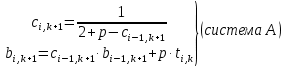 . (18) . (18)
Причем, система А предназначена для узлов (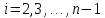 ). ).
Для узла i=1 из (13) найдем
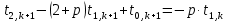 . (19) . (19)
Или, используя граничное условие (11), из (19) получим
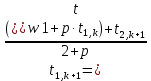 . (20) . (20)
С другой стороны, из (14) для узла i=1 найдем
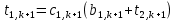 . (21) . (21)
Сравнивая (20) и (21), получим
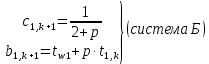 . (22) . (22)
Пользуясь формулами систем (А) и (Б), производя «прогонку» слева-направо в прямом направлении, последовательно определяют все коэффициенты 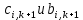 для всех внутренних точек-узлов для всех внутренних точек-узлов 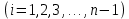 . .
Затем, используя «обратный ход», то есть прогонку справа-налево, начиная с 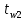 , как уже было указано, по (14) найдем все температуры в (k+1) слое, если известно распределение температур в k-м слое. Таким образом, указан переход от k-го слоя по времени к (k+1) слою. , как уже было указано, по (14) найдем все температуры в (k+1) слое, если известно распределение температур в k-м слое. Таким образом, указан переход от k-го слоя по времени к (k+1) слою.
Следовательно, отталкиваясь от известного начального (нулевого) слоя или начального распределения температур тела, можно найти решение 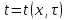 во всех точках сетки i,k. во всех точках сетки i,k.
Содержание отчета
Расчет температурного поля для трех шагов по времени с необходимыми пояснениями по явной схеме в пространственно-временной области.
Расчет температурного поля для трех шагов по времени с необходимыми пояснениями по программе на ЭВМ.
Сравнение результатов расчета п.1 и п.2.
Графическое представление результатов расчета по результатам п.2.
Расчет температурного поля для одного шага по времени с необходимыми пояснениями по неявной схеме, используя метод прогонки.
Расчет температурного поля для одного шага по времени с необходимыми пояснениями по неявной схеме, используя онлайн-калькулятор сети Интернет.
Сравнение результатов расчета п.4 и п.5.
Ответы на контрольные вопросы – тест по практическому занятию.
КОНТРОЛЬНЫЕ ВОПРОСЫ – ТЕСТ по практическому занятию №2
Укажите в правом столбце правильный ответ!
1)
choice
|
0
|
#3#
|
При нестационарной теплопроводности….
|
Температура в любой точке тела не зависит и не меняется с течением времени
|
0
|
Коэффициент теплопроводности не меняется у тела с течением времени
|
0
|
Температура в любой точке тела меняется с течением времени
|
1
|
2)
choice
|
0
|
#3#
|
Температурное поле одномерной области без внутренних источников теплоты описывается уравнением…
|
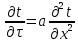
|
1
|
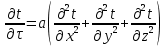
|
0
|
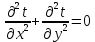
|
0
|
3)
choice
|
0
|
#3#
|
Одномерное плоское нестационарное температурное поле без внутренних источников теплоты описывается уравнением
|
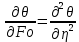
|
1
|
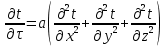
|
0
|
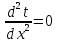
|
0
|
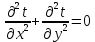
|
0
|
4)
choice
|
0
|
#3#
|
Одномерное цилиндрическое нестационарное температурное поле описывается уравнением
|
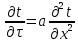
|
0
|
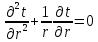
|
0
|
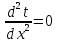
|
0
|
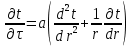
|
1
|
5)
choice
|
0
|
#3#
|
Укажите математическое выражение 3-мерного нестационарного температурного поля
|
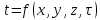
|
1
|
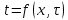
|
0
|
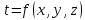
|
0
|
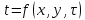
|
0
|
6)
choice
|
0
|
#3#
|
Укажите математическое выражение двухмерного нестационарного температурного поля
|
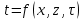
|
1
|
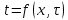
|
0
|
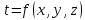
|
0
|
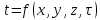
|
0
|
7)
choice
|
0
|
#3#
|
Укажите математическое выражение 1-мерного нестационарного температурного поля
|
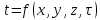
|
0
|
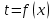
|
0
|
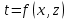
|
0
|
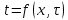
|
1
|
8)
choice
|
0
|
#3#
|
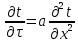 - это уравнение в обыкновенных производных? - это уравнение в обыкновенных производных?
|
Нет
|
1
|
Да
|
0
|
9)
choice
|
0
|
#3#
|
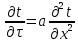 -можно ли это уравнение интегрировать? -можно ли это уравнение интегрировать?
|
Нет
|
1
|
Да
|
0
|
10)
choice
|
0
|
#3#
|
Какое из приведенных уравнений записано неверно?
|
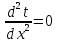
|
0
|
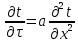
|
0
|
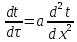
|
1
|
11)
choice
|
0
|
#3#
|
Какое из приведенных уравнений записано неверно?
|
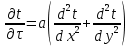
|
1
|
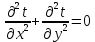
|
0
|
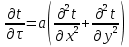
|
0
|
12)
choice
|
0
|
#3#
|
Математическая постановка одномерной задачи нестационарной теплопроводности включает в себя
|
Дифференциальное уравнение теплопроводности
Граничные условия на поверхности тела
|
0
|
Дифференциальное уравнение теплопроводности
Начальное условие
Граничные условия на поверхности тела
|
1
|
Начальные условия
Граничные условия на поверхности тела
Геометрические условия
|
0
|
13)
choice
|
0
|
#3#
|
Какое уравнение является заменой уравнения 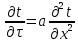 согласно метода конечных разностей по явной схеме согласно метода конечных разностей по явной схеме
|
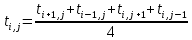
|
0
|
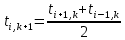
|
0
|
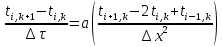
|
1
|
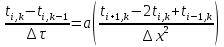
|
0
|
14)
choice
|
0
|
#3#
|
Какое уравнение является заменой уравнения 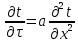 согласно метода конечных разностей по неявной схеме согласно метода конечных разностей по неявной схеме
|
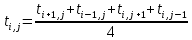
|
0
|
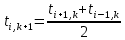
|
|
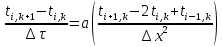
|
|
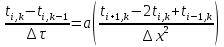
|
1
|
15)
choice
|
0
|
#3#
|
Если индекс «i» отвечает за шаг по координате, а индекс «k» за шаг по времени, то как понимать выражение 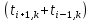 ? ?
|
Это сумма температур двух соседних узлов в настоящий и последующий момент времени
|
0
|
Это сумма температур двух соседних узлов в настоящий момент времени
|
1
|
Это сумма температур одного и того же узла, но в различные моменты времени
|
0
|
16)
choice
|
0
|
#3#
|
Если индекс «i» отвечает за шаг по координате, а индекс «k» за шаг по времени, то как понимать выражение 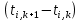 ? ?
|
Это разность температур двух соседних узлов в настоящий и последующий момент времени
|
0
|
Это разность температур одного и того же узла через один шаг по времени
|
1
|
Это разность температур двух соседних узлов через один шаг по времени
|
0
|
17)
choice
|
0
|
#3#
|
Если индекс «i» отвечает за шаг по координате, а индекс «k» за шаг по времени, то как понимать выражение 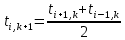 ? ?
|
Температура в данном узле – это среднеарифметическое между температурами в двух соседних узлах предыдущего момента времени
|
1
|
Температура в узле предыдущего момента времени определяется как сумма температур двух соседних узлов последующего момента времени
|
0
|
Температура в данном узле момента времени «k+1» - это есть сумма температур соседних узлов в момент времени «k».
|
0
|
18)
choice
|
0
|
#3#
|
Ограничивается ли шаг по времени 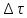 в явной схеме метода конечных разностей? в явной схеме метода конечных разностей?
|
Нет, шаг по времени можно выбрать любой, если расчет проводить сразу для всех узлов сетки, решая полученную систему линейных алгебраических уравнений
|
0
|
Да, шаг по времени ограничен, если принять условие 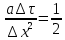 , которое приводит к существенному упрощению расчета температуры в узле сетки. , которое приводит к существенному упрощению расчета температуры в узле сетки.
|
1
|
19)
choice
|
0
|
#3#
|
Шаг по времени в явной схеме, при расчете температуры в узле по формуле 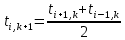 , должен ли быть обязательно равен выражению , должен ли быть обязательно равен выражению 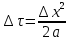 ? ?
|
Да, для явной схемы он определяется только по этому выражению
|
0
|
Нет, об может быть выбран и меньше полученного значения 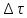
|
1
|
Нет, для явной схемы шаг по времени может быть выбран любым
|
0
|
20)
choice
|
0
|
#3#
|
Ограничивается ли шаг по времени 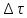 в неявной схеме метода конечных разностей? в неявной схеме метода конечных разностей?
|
Нет, шаг по времени можно выбрать любой, так как расчет проводится сразу для всех узлов сетки
|
1
|
Да, шаг по времени ограничен, если принять условие 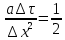 , которое приводит к существенному упрощению расчета температуры в узле сетки. , которое приводит к существенному упрощению расчета температуры в узле сетки.
|
0
|
21)
choice
|
0
|
#3#
|
Почему одна из схем в методе конечных разностей называется «явной»?
|
Так как при замене дифференциального уравнения теплопроводности на уравнение в конечных разностях в полученном алгебраическом уравнении всего одна неизвестная, которую можно сразу определить
|
1
|
Так как полученное решение оказывается очень простым для последующих расчетов
|
0
|
Так как зависимость между температурой в последующий момент времени явным образом связана с температурой в предыдущий момент времени
|
0
|
22)
choice
|
0
|
#3#
|
Почему одна из схем в методе конечных разностей называется «неявной»?
|
Так как зависимость между температурой в последующий момент времени неявным образом связана с температурой в предыдущий момент времени
|
0
|
Так как при нахождении решения дифференциального уравнения нужно задействовать метод разделения переменных Фурье
|
0
|
Так как при замене дифференциального уравнения теплопроводности на уравнение в конечных разностях в полученном алгебраическом уравнении два или три неизвестных, которые сразу определить невозможно
|
1
|
23)
choice
|
0
|
#3#
|
Как определяется шаг по координате в случае одномерной нестационарной задачи теплопроводности?
|
Шаг по координате – это отношение длины тела на количество шагов по времени
|
0
|
Шаг по координате – это отношение длины тела на количество разбиваемых частей
|
1
|
24)
choice
|
0
|
#3#
|
Укажите «плюсы» и «минусы» явной схемы.
|
«плюсы» - простота, легкий расчет;
«минусы» - зависит от шага по времени, который может быть относительно малым, вследствие чего количество расчетов многократно может возрасти. Если же шаг по времени выбрать более чем 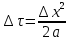 , то расчет вообще получится неверным. , то расчет вообще получится неверным.
|
1
|
«Плюсы» - нет зависимости от шага по времени, т.е. шаг по времени выбирается любой, и расчет получается достаточно точным;
«минусы» - схема расчета достаточно сложна, приходится применять дополнительные знания по решению системы алгебраических уравнений
|
0
|
25)
choice
|
0
|
#3#
|
Укажите «плюсы» и «минусы» неявной схемы.
|
«плюсы» - простота, легкий расчет;
«минусы» - зависит от шага по времени, который может быть относительно малым, вследствие чего количество расчетов многократно может возрасти. Если же шаг по времени выбрать более чем 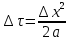 , то расчет вообще получится неверным. , то расчет вообще получится неверным.
|
0
|
«Плюсы» - нет зависимости от шага по времени, т.е. шаг по времени выбирается любой, и расчет получается достаточно точным;
«минусы» - схема расчета достаточно сложна, приходится применять дополнительные знания по решению системы алгебраических уравнений
|
1
|
26)
choice
|
0
|
#3#
|
Какая из схем является устойчивой, т.е. ошибки при неточном задании краевых условий и округления не будут влиять на конечный результат?
|
Явная схема
|
0
|
Неявная схема
|
1
|
27)
choice
|
0
|
#3#
|
Как определить коэффициент температуропроводности?
|
Это есть отношение коэффициента теплопроводности на произведение изобарной теплоемкости на плотность вещества
|
1
|
Это есть отношение изобарной теплоемкости на коэффициент теплопроводности
|
0
|
28)
choice
|
0
|
#3#
|
При замене дифференциального уравнения теплопроводности на уравнение в конечных разностях согласно неявной схеме сколько узлов связаны полученной алгебраической зависимостью?
|
Два соседних узла
|
0
|
Три соседних узла
|
1
|
Четыре соседних узла
|
0
|
29)
choice
|
0
|
#3#
|
Согласно метода прогонки между собой связываются… через коэффициенты «а» и «в»
|
Два соседних узла
|
1
|
Три соседних узла
|
0
|
Четыре соседних узла
|
0
|
30)
choice
|
0
|
#3#
|
В чем суть метода прогонки?
|
Определение коэффициентов связи «а» и «в» слева-направо и затем определение температур в узлах, используя эти коэффициенты, справо-налево.
|
1
|
Необходимо записать систему алгебраических линейных уравнений таким образом, чтобы потом, используя онлайн-калькулятор сети Интернет, решить полученную систему
|
0
|
Приложение 1

Образец титульного листа отчета
Приложение 2 |
|
|
 Скачать 323.57 Kb.
Скачать 323.57 Kb.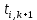 и
и 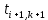 в виде
в виде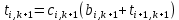 , (14)
, (14)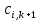 и
и 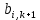 некоторые коэффициенты, подлежащие определению. Если они будут известны, то делая «прогонку» в направлении справа-налево, начиная с правого граничного условия
некоторые коэффициенты, подлежащие определению. Если они будут известны, то делая «прогонку» в направлении справа-налево, начиная с правого граничного условия 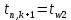 , можно по (14) последовательно найти все температуры в (k+1)-м слое по времени. Из (14), заменяя i на i-1, имеем
, можно по (14) последовательно найти все температуры в (k+1)-м слое по времени. Из (14), заменяя i на i-1, имеем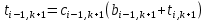 , (15)
, (15)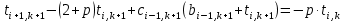 . (16)
. (16)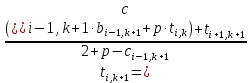 . (17)
. (17)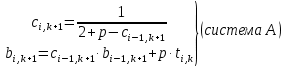 . (18)
. (18)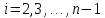 ).
).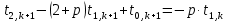 . (19)
. (19)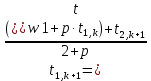 . (20)
. (20)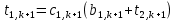 . (21)
. (21)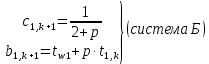 . (22)
. (22)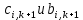 для всех внутренних точек-узлов
для всех внутренних точек-узлов 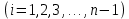 .
.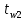 , как уже было указано, по (14) найдем все температуры в (k+1) слое, если известно распределение температур в k-м слое. Таким образом, указан переход от k-го слоя по времени к (k+1) слою.
, как уже было указано, по (14) найдем все температуры в (k+1) слое, если известно распределение температур в k-м слое. Таким образом, указан переход от k-го слоя по времени к (k+1) слою.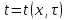 во всех точках сетки i,k.
во всех точках сетки i,k.

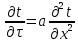
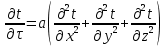
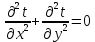
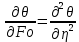
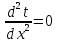
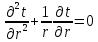
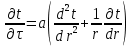
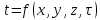
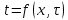
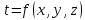
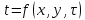
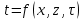
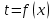
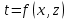
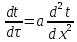
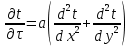
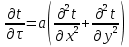
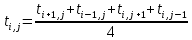
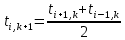
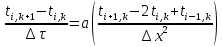
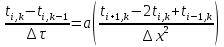
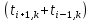 ?
?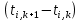 ?
?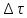 в явной схеме метода конечных разностей?
в явной схеме метода конечных разностей?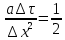 , которое приводит к существенному упрощению расчета температуры в узле сетки.
, которое приводит к существенному упрощению расчета температуры в узле сетки.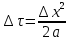 ?
?