Пособие для первого курса Колоколов 2014. Методические указания к решению задач для студентов iго курса дневного отделения Москва 2014 удк колоколов А. А
 Скачать 1.77 Mb.
|
|
Министерство образования и науки Российской Федерации Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Московский государственный технологический университет «Станкин» Кафедра «Физика» А.А. Колоколов «Механика и молекулярная физика» Методические указания к решению задач для студентов I-го курса дневного отделения Москва 2014 УДК Колоколов А.А. А.А.Колоколов. – М.: ГОУ ВПО МГТУ «СТАНКИН», 2014. – __с. Методические указания предназначены для студентов первого курса… УДК © Колоколов А.А. © ГОУ ВПО МГТУ «Станкин», 2014 1. Динамика материальной точки В классической нерелятивистской механике, где скорость движения тел считается много меньше скорости света в вакууме  , основным законом динамики является II-ой закон Ньютона. Согласно этому закону в инерциальной системе отсчета первая производная импульса  тела по времени  равна полной силе  , действующей на это тело,
Здесь  , m – инертная масса тела,  - мгновенная скорость тела,  - радиус-вектор тела, определяющий его положение в выбранной инерциальной системе отсчета.При определении мгновенной скорости тело рассматривается как материальная точка, т.е. линейные размеры тела считаются малыми по сравнению с характерными расстояниями решаемой задачи и не учитывается вращательное движение тела. Если масса тела m при движении сохраняется постоянной, уравнение (1.0.1) упрощается и принимает вид
где  - мгновенное ускорение тела. Это обыкновенное дифференциальное уравнение второго порядка по времени. Для однозначного определения решения уравнения (1.0.2), т.е. нахождения функции , необходимо в некоторый момент времени  задать два начальных условия:
В этом случае при заданной силе все последующие состояния тела  ,  для  находятся однозначно.Определение движения тела по заданным начальным условиям и известной силе называется прямой задачей динамики. В обратной задаче требуется найти силу, которая обеспечивает необходимые характеристики движения тела (это задача управления движением тела). Задача № 1 Два тела с массами m1 и m2 связаны между собой нерастяжимой и невесомой (m=0) нитью, перекинутой через невесомый блок (рис.1.1). Коэффициент трения скольжения между телом 1 и горизонтальной поверхностью μ=0,2. Ускорение свободного падения g=9,8м/с2. Блок считается невесомым. Трением в блоке можно пренебречь. Определить ускорения тел a1 и a2, если в начальный момент времени t=0 они были неподвижны. Рассмотреть два случая: 1)m1=10кг, m2=5кг; 2) m1=10кг, m2=1кг. 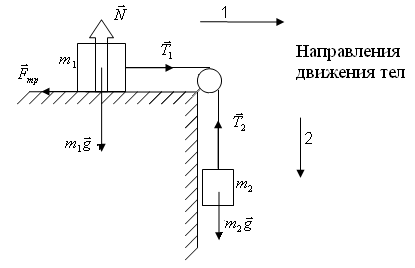 Рис.1.1 Решение Это прямая задача динамики, где по заданным действующим силам необходимо рассчитать движение тел в системе с кинематическими связями. Решение задачи выполняется с помощью следующего алгоритма. 1. Укажем все силы, которые согласно условиям задачи действуют на тела системы с отличной от нуля массой (движение невесомых тел определяется связями): силы тяжести  и  , силы натяжения  и  , сила реакции опоры  , сила трения  .2. Согласно II-ому закону Ньютона запишем в векторной форме уравнения движения тел 1 и 2:
3. Поскольку тела движутся вдоль прямых, то удобно перейти от векторных уравнений к одномерным скалярным уравнениям, используя проекции уравнений (1.1.1)-(1.1.2) на направления соответствующих движений:
В полученные 3 уравнения входят 6 неизвестных величин: a1, a2, T1, T2, N и Fтр. Для однозначного нахождения всех 6 неизвестных систему уравнений (1.1.3)-(1.1.5) необходимо дополнить еще тремя независимыми уравнениями. 4. Для получения дополнительных уравнений воспользуемся условиями задачи и законами физики. Поскольку нить нерастяжима, то величины ускорений должны быть одинаковыми:
Нить и блок считаются невесомыми, трение в блоке не учитывается, поэтому величины сил натяжения равны друг другу во всех точках нити:
Сила трения имеет различную физическую природу и величину в зависимости от того, движется тело 1 относительно поверхности или нет:
Здесь Fтр.п. – сила трения покоя и Fтр.ск. – сила трения скольжения. В зависимости от условий задачи возможны два решения. I. Допустим, что действующие силы обеспечивают движение тел и
В этом случае полная система уравнений принимает вид:
Решая эту систему равнений, получим:
Данное решение справедливо, если a>0 или m2>μm1. Физический смысл последнего условия заключается в том, что сила тяжести m2g, действующая на тело 2, должна превышать максимальное значение силы трения покоя  =Fтр.ск.=μN=μm1g, действующей на тело 2 и препятствующей движению.II. Если m2<μm1, тела остаются в состоянии покоя и
Соответствующая полная система уравнений принимает вид (  ):
Решение этой системы дает:
Для m1=10кг, m2=5кг и μ=0,2 справедливо условие m2>μm1, поэтому тела движутся с ускорением
При m1=10кг, m2=1кг и μ=0,2 выполняется условие m2<μm1, сила трения покоя Fтр.п.=m2g и тела остаются в состоянии покоя, когда
Ответ: 1) 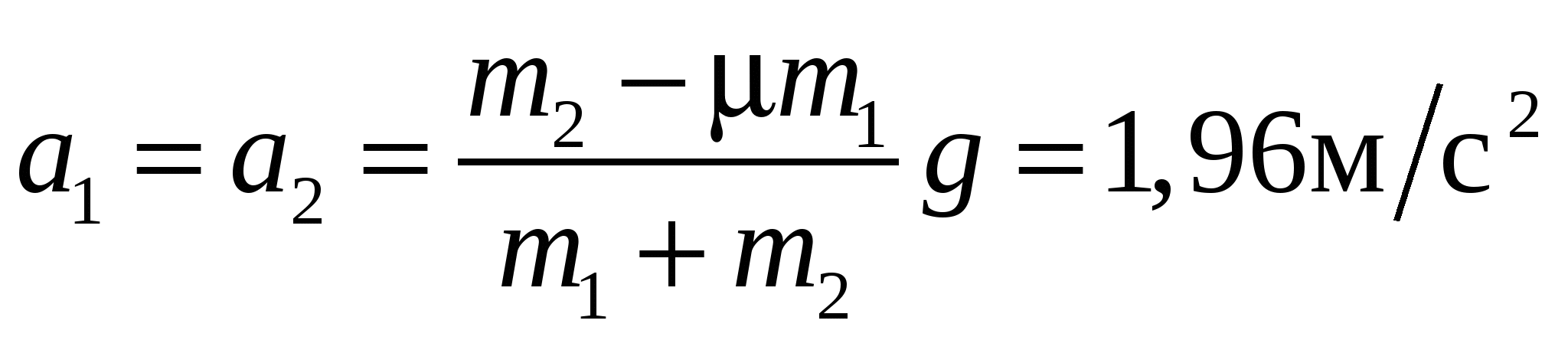 ; 2) .Задача №2 На краю горизонтального диска радиусом R=0,1м неподвижно лежит маленькая шайба (рис.2.1). В момент времени t=0 диск начинает вращаться вокруг вертикальной оси, проходящей через его центр, с угловым ускорением ε=1рад/с2. Через какое время t1 шайба соскользнет с диска, если коэффициент скольжения между шайбой и поверхностью диска μ=0,2? 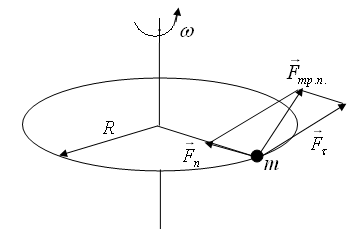 Рис.2.1 Угловая скорость ω и угловое ускорение ε определяются следующим образом
где φ - угол поворота диска вокруг вертикальной оси. Шайба совершает ускоренное движение по окружности, где её ускорение  удобно представить в виде векторной суммы.
Здесь  – тангенциальное ускорение, направленное по касательной к окружности
где  - единичный вектор касательной к окружности, направленный по вектору линейной скорости  . Это ускорение определяет скорость изменения величины линейной скорости  . Ускорение  – нормальное ускорение, перпендикулярное к касательной окружности в точке нахождения шайбы и направленное к центру окружности
Единичный вектор нормали  перпендикулярен к вектору и направлен к центру окружности. Нормальное ускорение определяет скорость изменения направления вектора .Решение Это пример обратной задачи динамики, где по заданному ускорению тела требуется найти необходимую силу. 1. Определим все силы, которые действуют на шайбу согласно условиям задачи: сила тяжести  , сила реакции опоры  и сила трения покоя  (шайба считается неподвижной относительно поверхности диска).2. Запишем в векторной форме уравнение движения шайбы в лабораторной системе отсчета:
Поскольку ускорение шайбы в вертикальном направлении равно нулю, то
и уравнение (1.2.5) упрощается:
Используя разложение полного ускорения шайбы на тангенциальное  и нормальное ускорения, запишем уравнение (1.2.7) в виде:
где  .3. Перейдем от векторной формы записи уравнения (1.2.8) к скалярной, используя проекции на направления ускорений и ,
4. Определим зависимость величины полного ускорения шайбы
от времени. Согласно определению
Здесь использована известная формула для линейной скорости материальной точки, движущейся по окружности,  . Нормальное ускорение определяется выражением
в которое входит неизвестная угловая скорость ω(t). Для нахождения ω(t) используем определение углового ускорения
Разделим в этом дифференциальном уравнении относительно угловой скорости переменные ω и
и проинтегрируем левую часть по времени от t=0 до текущего момента времени t, а правую часть по угловой скорости от начального значения 0 до текущего значения ω(t)
Выполняя интегрирование
и подставляя (1.2.16) в (1.2.10), найдем, что
Из (1.2.10), (1.2.11) и (1.2.17) следует, что величина полного ускорения
монотонно растет со временем. 5. В соответствии с ростом величины ускорения должна расти сила трения покоя, обеспечивающая это ускорение,
Однако величина силы трения покоя ограничена сверху величиной силы трения скольжения Fтр.ск.=μN=μmg :
поэтому условие движения шайбы вместе с диском принимает вид
Отсюда находим, что в момент времени t1, когда
шайба слетит с диска. Таким образом,
Отметим, что при μg<Rε шайба слетит с диска сразу после начала вращения. Ответ: t1=4,5с. |
.
,
, 
.
,
.
,
,
.
.
,
.
,
,
,
.
,
.
, 
.
.
.
.
, 
, 
.
,
.
.
.
.
.
,
.
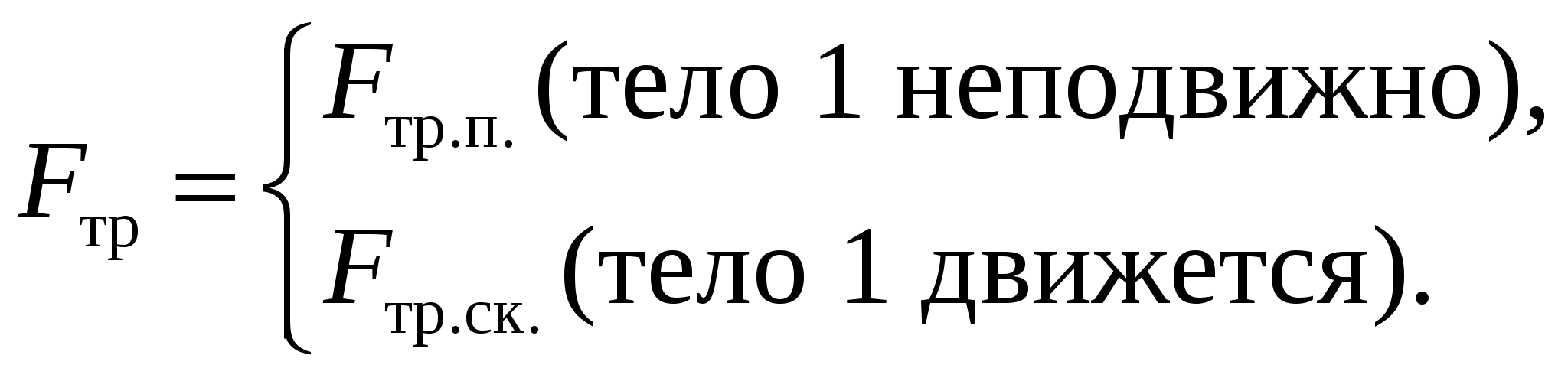
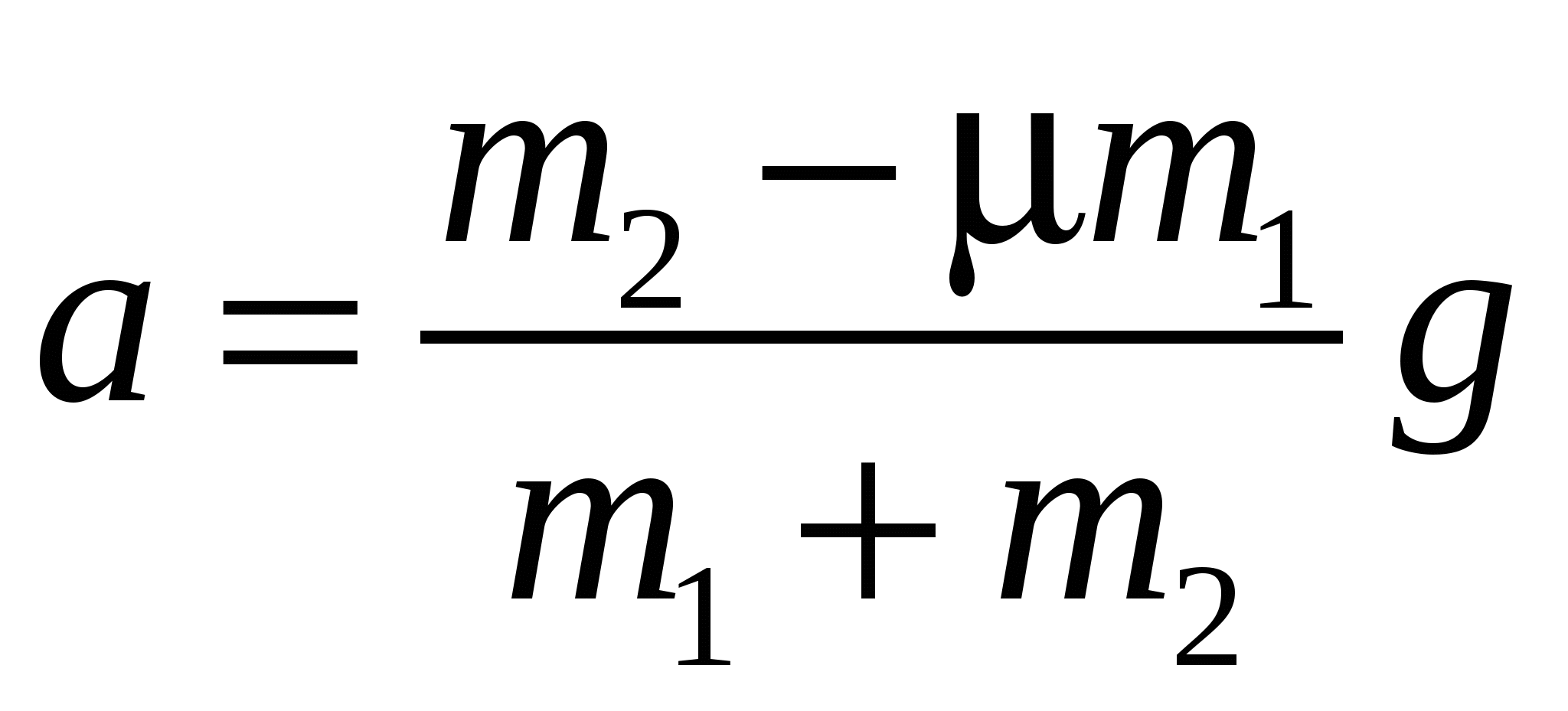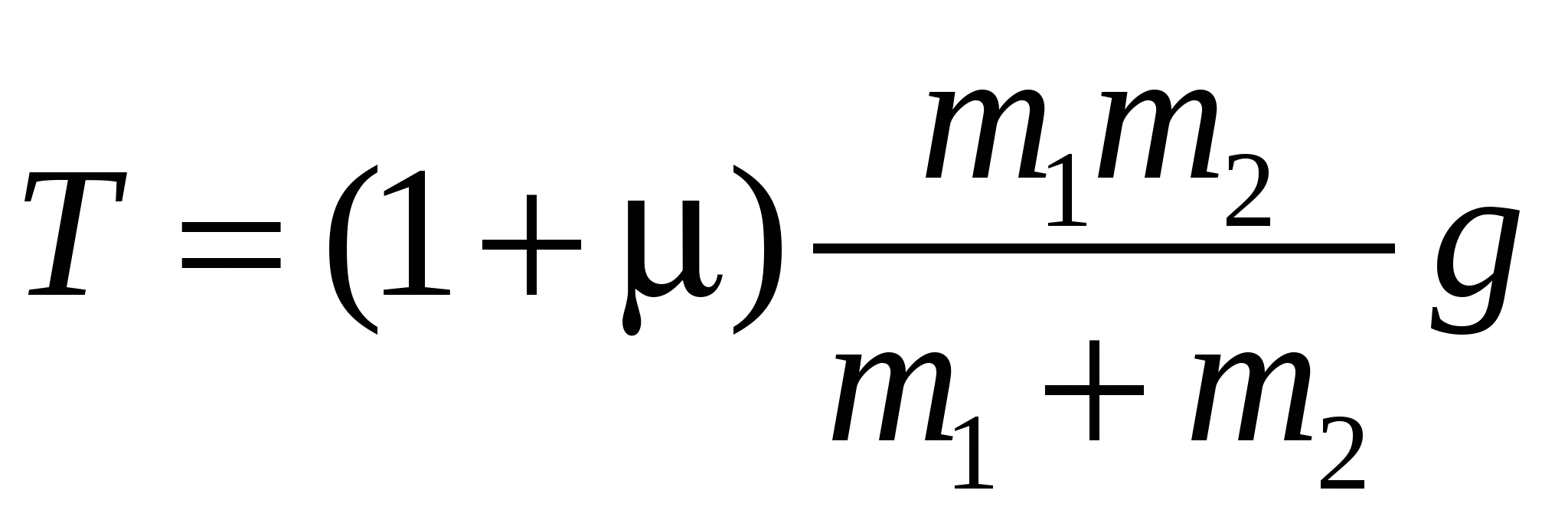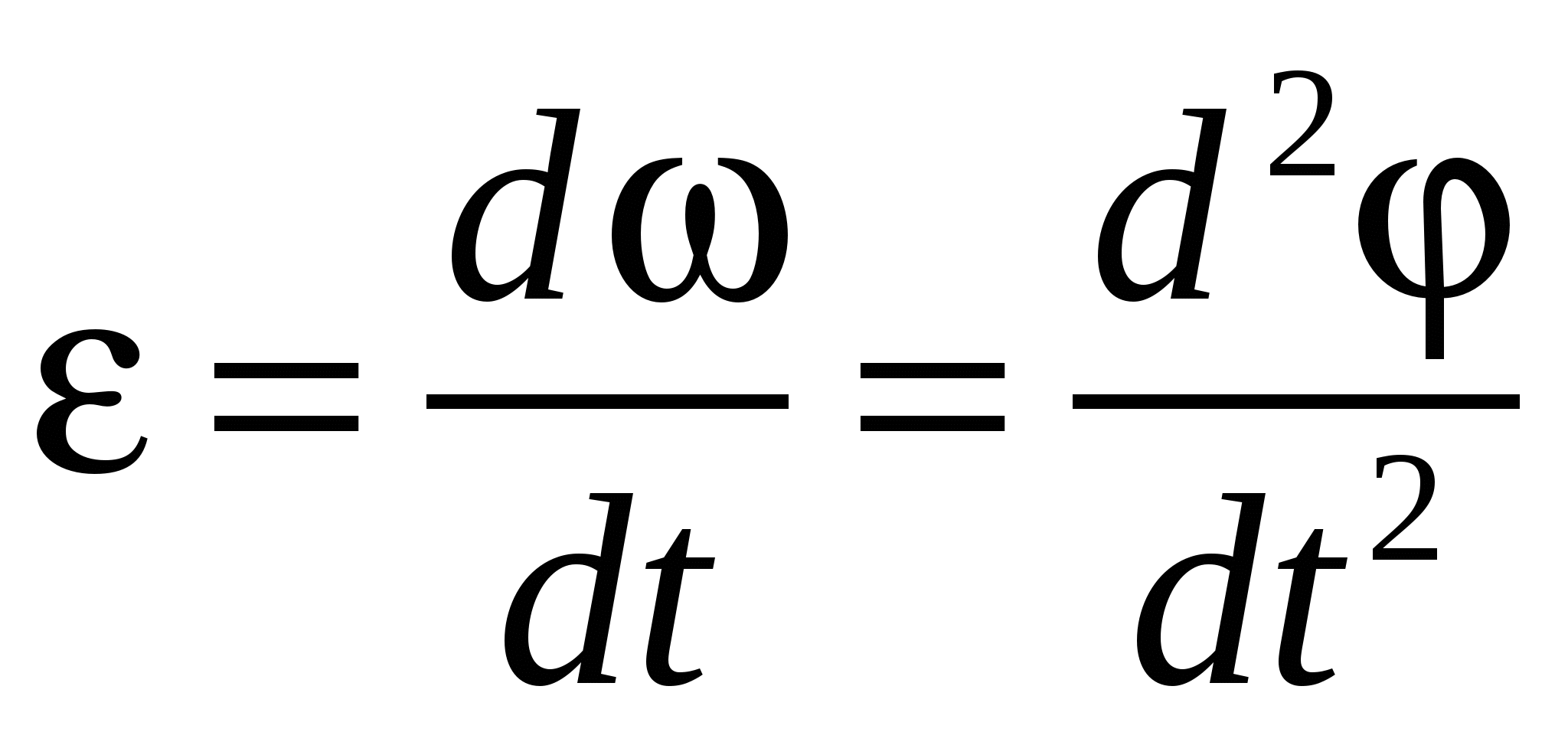
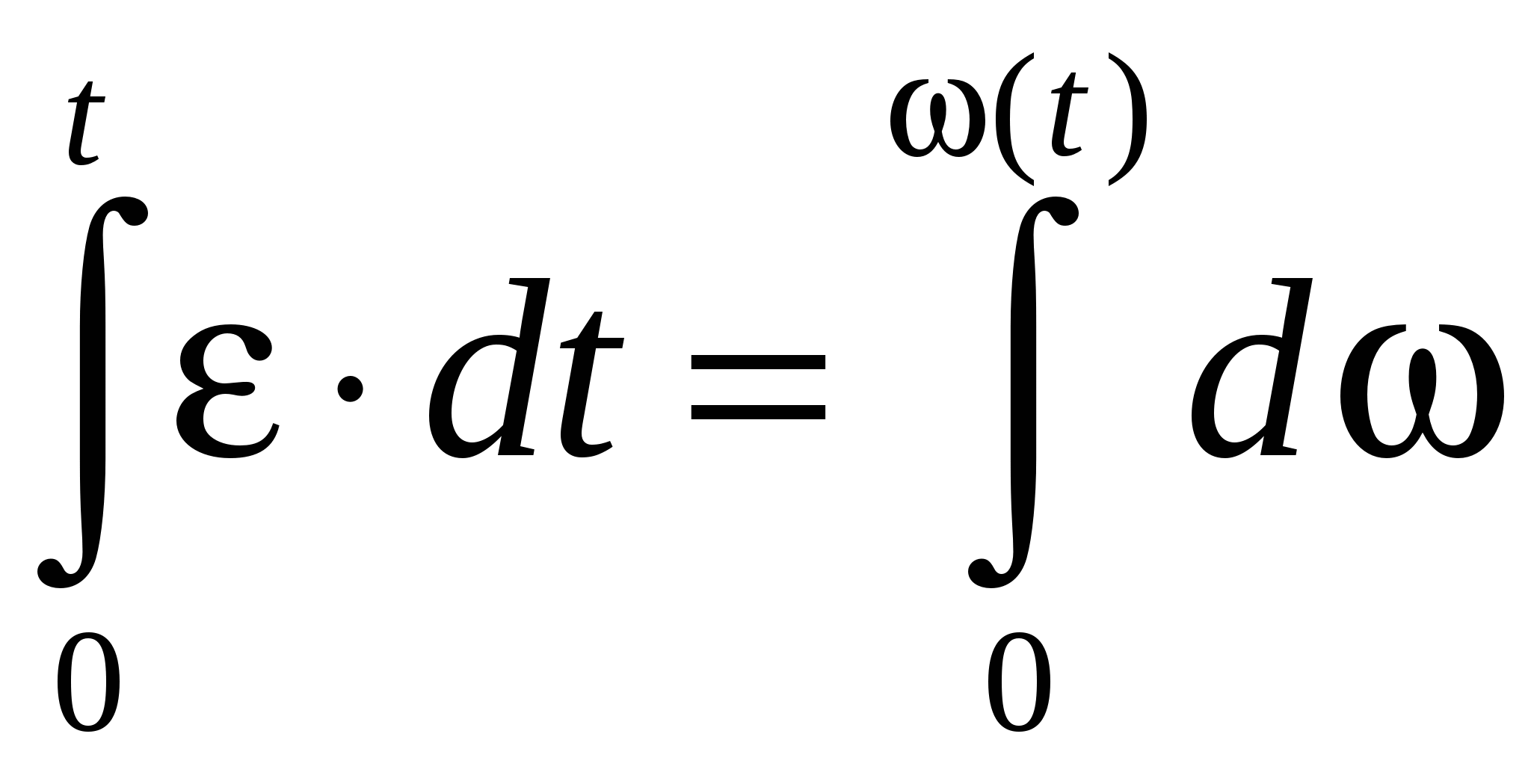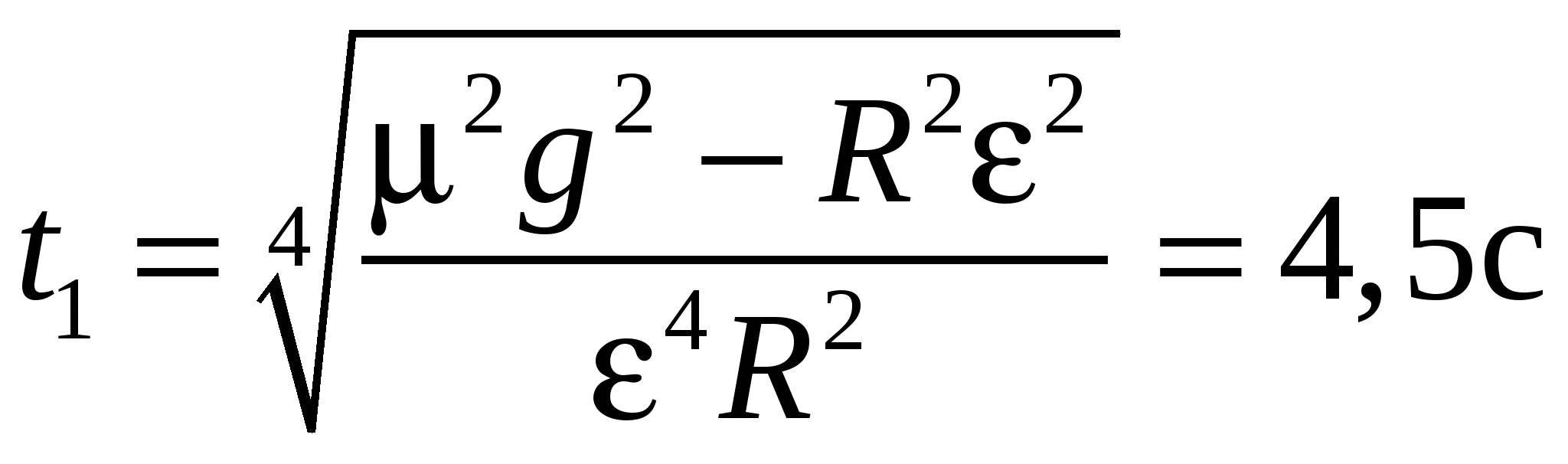