Пособие для первого курса Колоколов 2014. Методические указания к решению задач для студентов iго курса дневного отделения Москва 2014 удк колоколов А. А
 Скачать 1.77 Mb. Скачать 1.77 Mb.
|
|
Рис. 3.02 Точка О – точка пересечения плоскости, проходящей через точку O´ приложения силы Для описания вращения твердого тела вокруг неподвижной оси используется уравнение моментов относительно этой оси
где
- момент импульса твердого тела относительно оси вращения, I – момент инерции твердого тела относительно этой оси, ω - угловая скорость вращения твердого тела и Если при вращении твердого тела его момент инерции сохраняется постоянным, уравнение моментов относительно неподвижной оси упрощается и принимает вид:
где
-угловое ускорение твердого тела и φ - угол поворота твердого тела вокруг оси вращения. Из уравнения моментов относительно неподвижной оси следует, что момент импульса относительно этой оси сохраняется постоянным
если полный момент всех внешних сил, действующих на твердое тело, относительно рассматриваемой оси равен нулю
Кинетическая энергия Kтвердого тела, вращающегося вокруг неподвижной оси, описывается выражением
Изменение кинетической энергии K может быть обусловлено работой как внешних, так и внутренних сил, поэтому
При повороте абсолютно твердого тела на бесконечно малый угол Δφ работа внешних сил
Если полный момент внешних сил, действующих на тело равен нулю, то изменение кинетической энергии вращающегося тела возможно за счет работы внутренних сил, которая меняет момент инерции твердого тела
Здесь L = const, поскольку Мвнешн= 0. Задача №7 В устройстве, показанном на рис.7.1, определите ускорения тел с массами m1 и m2 (m1 > m2), связанных невесомой, нерастяжимой нитью, перекинутой через блок. Блок представляет собой однородный цилиндр с массой М и радиусом R. Нить по блоку не проскальзывает, трение в оси блока пренебрежимо мало. Ускорение свободного падения g. 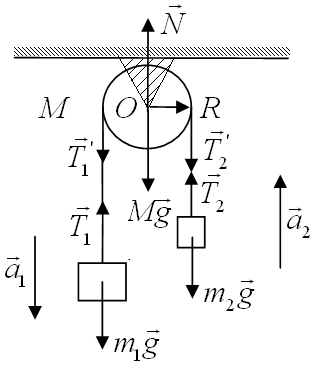 Рис.7.1 Решение 1. Определим все силы, действующие на тела системы с отличной от нуля массой: силы тяжести 2. Запишем в векторной форме уравнения поступательного движения тел 1 и 2
Для блока поступательное движение отсутствует, поэтому
Блок совершает вращательное движение вокруг своей оси симметрии, проходящей через центр масс блока перпендикулярно плоскости рисунка. Уравнение моментов относительно оси вращения блока имеет вид
где момент инерции однородного блока относительно его оси симметрии
3. Перейдем от векторной формы записи уравнений (3.7.1) - (3.7.2) к скалярной, используя проекции этих уравнений на направления ускорений тел
которая содержит 7 неизвестных величин: 4. Получим полную систему из 7 независимых уравнений, используя законы физики и условия задачи. Благодаря нерастяжимости нити величины ускорений тел одинаковые:
Поскольку нить не проскальзывает по поверхности блока, то в каждой точке контакта линейные скорости элементов нити υ и поверхности блока ωR равны по величине
Отсюда получаем, что величины ускорения a тел и углового ускорения ε блока связаны соотношением
Согласно условию задачи нить невесомая, поэтому сила натяжения одинаковая во всех точках нити слева от блока
и во всех точках нити справа от блока
На основе уравнений (3.7.6) – (3.7.13) приходим к полной системе из 4 независимых уравнений для нахождения 4 неизвестных величин:
5. Решая систему уравнений (3.7.14) – (3.7.17), находим величину ускорения тел
Согласно полученному результату учет массы блока уменьшает ускорение тел. Ответ: 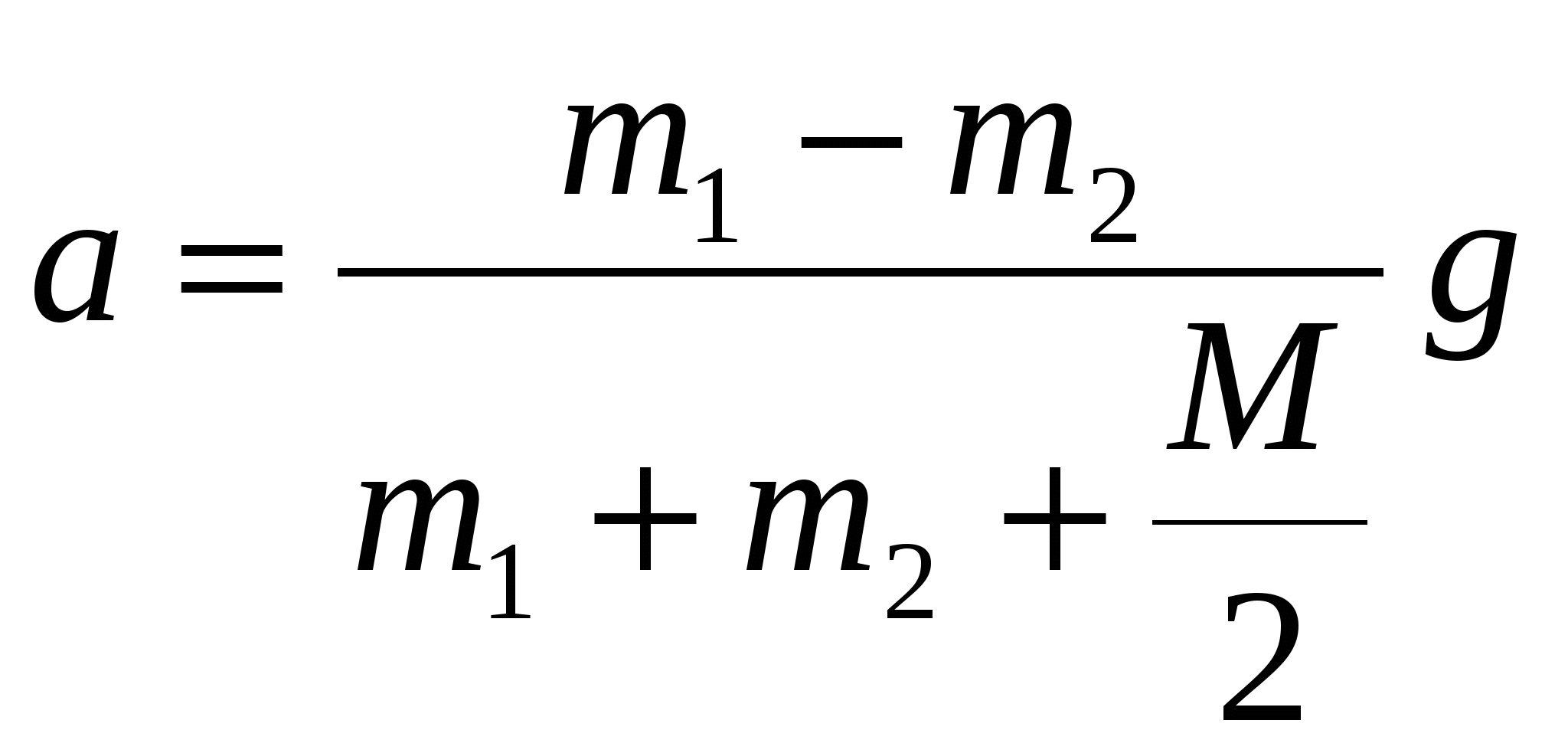 . .Задача №8 Маховик в виде однородного диска с массой m=10кг и радиусом R=0,2м вращается вокруг своей оси симметрии с начальной угловой скоростью ω0=100рад/с. В момент времени t=0 к маховику начинают прижимать две тормозные колодки с силой F=50H каждая (рис.17.1). Коэффициент трения скольжения между маховиком и тормозными колодками μ=0,3. Определите изменение во времени угловой скорости ω(t) вращения маховика. Через какое время t1 маховик остановиться? 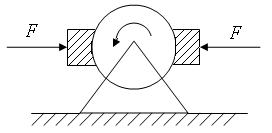 Рис.8.1 Решение Уравнение моментов относительно оси вращения маховика имеет вид
где μF – сила трения скольжения между маховиком и тормозной колодкой и
-момент инерции маховика относительно его оси симметрии. Разделим переменные ω и t в дифференциальном уравнении (3.8.1)
и проинтегрируем левую часть полученного равенства по ω от начальной угловой скорости ωо до текущей угловой скорости ω(t), а правую часть по t от начального момента времени t=0до текущего момента t
Выполняя интегрирование, получим зависимость угловой скорости маховика от времени
Время t1, через которое маховик остановится, находится с помощью уравнения
Отсюда следует, что время остановки маховика
Ответ: Задача №9 Однородный цилиндр массой с m и радиусом R скатывается без проскальзывания по наклонной плоскости с углом наклона α относительно горизонтали (рис.9.1). Ускорение свободного падения g. Определите ускорение 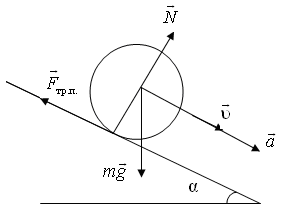 Рис.9.1 Решение 1.Определим все силы, которые действуют на цилиндр согласно условиям задачи: сила тяжести 2. Запишем уравнение движения центра масс цилиндра в векторной форме
Кроме поступательного движения цилиндр совершает вращение вокруг своей оси симметрии с угловой скоростью ω, которая меняется со временем. Соответствующий вращающий момент создает только сила трения покоя, поскольку векторы силы тяжести и силы реакции опоры проходят через ось вращения и поэтому их вращающие моменты равны нулю. Поскольку ось вращения перемещается в пространстве таким образом, что все время остается параллельной самой себе в разные моменты времени, то уравнение моментов записывается точно так же, как для неподвижной оси:
где
- момент инерции однородного цилиндра относительно его оси симметрии. 3. Перейдем от векторной формы записи уравнения (3.9.1) к скалярной, используя проекции на направление вектора ускорения
При этом выполняется равенство
поскольку центр масс цилиндра не имеет ускорения в направлении, перпендикулярном к наклонной плоскости. Уравнения поступательного (3.9.4), (3.9.5) и вращательного (3.9.2) движений цилиндра содержат 4 неизвестных величины: a, N, 4. Согласно условиям задачи цилиндр скатывается без проскальзывания, поэтому в области касания поверхности цилиндра с наклонной плоскостью скорость элементов поверхности цилиндра равна нулю и поэтому справедливо соотношение
где υ - скорость поступательного движения цилиндра, равная скорости движения центра масс, и ωR - линейная скорость элементов поверхности цилиндра, связанная с его вращением вокруг оси симметрии. Дифференцируя уравнение (3.9.6) по времени, получим связь между величинами линейного ускорения a и углового ускорения цилиндра ε
Таким образом, полная система уравнений для 4 неизвестных величин имеет вид:
5. Решая систему уравнений (3.9.8) – (3.9.11), получим
Сила трения покоя не должна превышать силу трения скольжения, поэтому должно выполняться условие
или
Только при выполнении условия (3.9.14) возможно скатывание цилиндра без проскальзывания. Ответ: Молекулярная физика. 4. Первое начало термодинамики Согласно первому началу термодинамики при обратимых процессах энергообмена между системой и окружающей средой количество теплоты Здесь макроскопическая работа определяется формулой 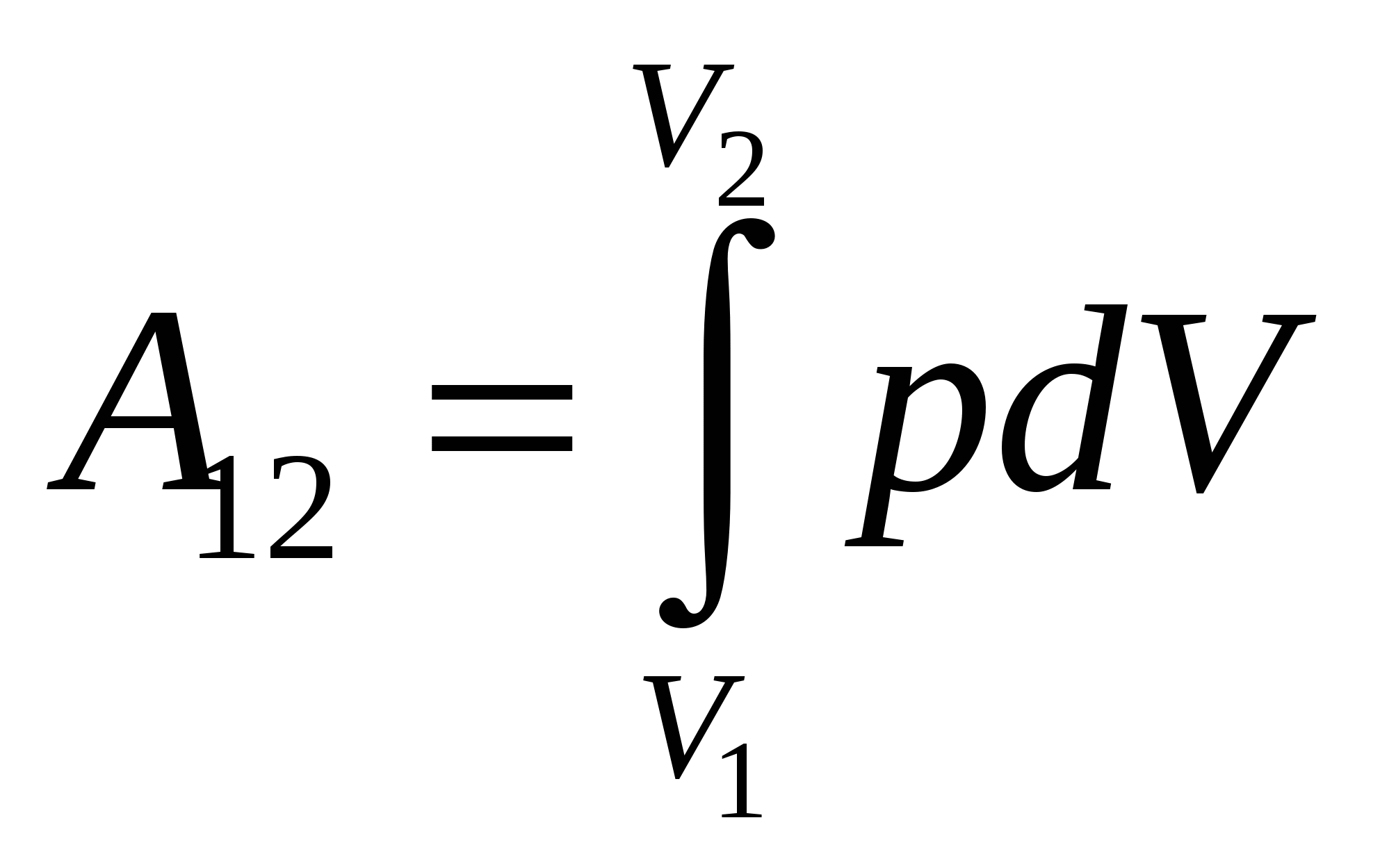 , ,где p – давление, V – объем, индексы 1 и 2 обозначают соответственно начальное и конечное равновесное состояние системы. Внутренняя энергия идеального одноатомного газа зависит только от температуры T газа и описывается выражением где Уравнение состояние идеального газа (уравнение Клапейрона - Менделеева) имеет вид: где Задача №10 Определить изменение внутренней энергии Решение Задача решается на основе формулы для внутренней энергии 1 моля идеального одноатомного газа с использованием уравнения Клапейрона – Менделеева при Согласно (1.1) изменение внутренней энергии обусловлено изменением температуры где Подставляя (1.4) в (1.3), получим В процессе изобарного расширения газ совершил работу и получил извне количество теплоты Ответ: Конструкция любой тепловой машины содержит нагреватель, рабочее тело и холодильник. За один цикл рабочее тело получает от нагревателя количество теплоты Затем цикл повторяется. Цикл Карно состоит из двух изотерм и двух адиабат, изображенных на диаграмме pV. 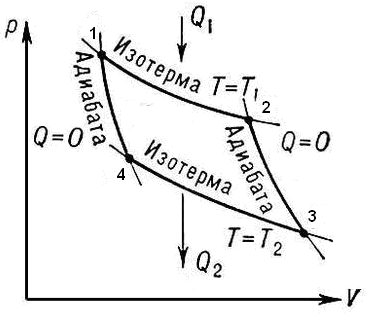 Здесь 1 – начальное равновесное состояние рабочего тела. Участок 12 – изотермическое расширение рабочего тела при температуре нагревателя а коэффициент полезного действия идеальной тепловой машины описывается формулами (определение к.п.д. с использованием первого начала термодинамики и равенства Клаузиуса для идеальной тепловой машины, работающей по циклу Карно). Задача№11 Идеальная тепловая машина, работающая по циклу Карно, получает теплоту от нагревателя с температурой Решение Задача решается с помощью формулы, которая выражает закон сохранения энергии для идеальной тепловой машины, работающей по циклу Карно, и равенства Клаузиуса для обратимых процессов где Исключая из системы уравнений (3.1) и (3.2) где Ответ: 5. Второе начало термодинамики Энтропия S как функция равновесного состояния термодинамической системы вводится на основе равенства Клаузиуса для обратимых круговых процессов. Здесь Согласно определению разность энтропии Интеграл в правой части вычисляется для любого обратимого процесса, переводящего систему из равновесного состояния 1 в равновесное состояние 2. С помощью первого начала термодинамики интеграл в правой части можно переписать следующим образом где U - внутренняя энергия системы, p - давление и V - объём. В классической термодинамике определяется только разность энтропии в двух произвольных равновесных состояний, поэтому энтропия равновесного состояния задана с точностью до постоянной. Размерность энтропии в СИ Дж/К. Задача №12 Определить изменение Решение Задача решается на основе определения энтропии уравнение Клапейрона - Менделеева для 1 моля идеального газа и формулы, описывающей внутреннюю энергию 1 моля одноатомного идеального газа, где
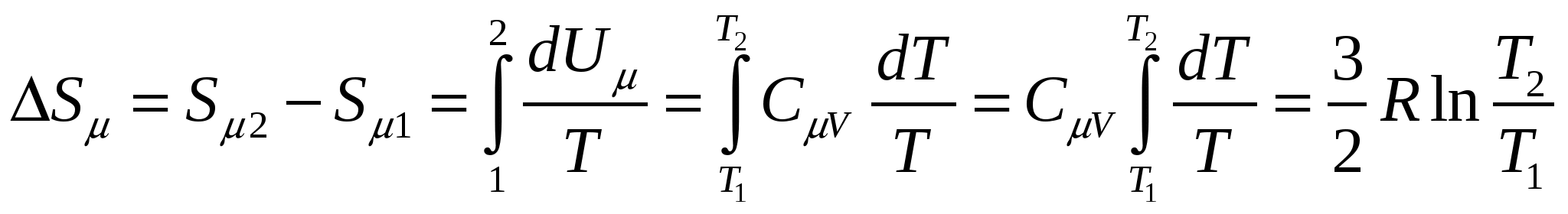 , (5.12.4) , (5.12.4)где
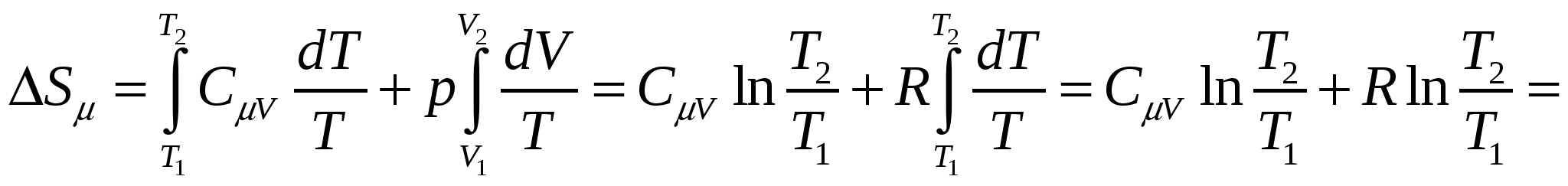 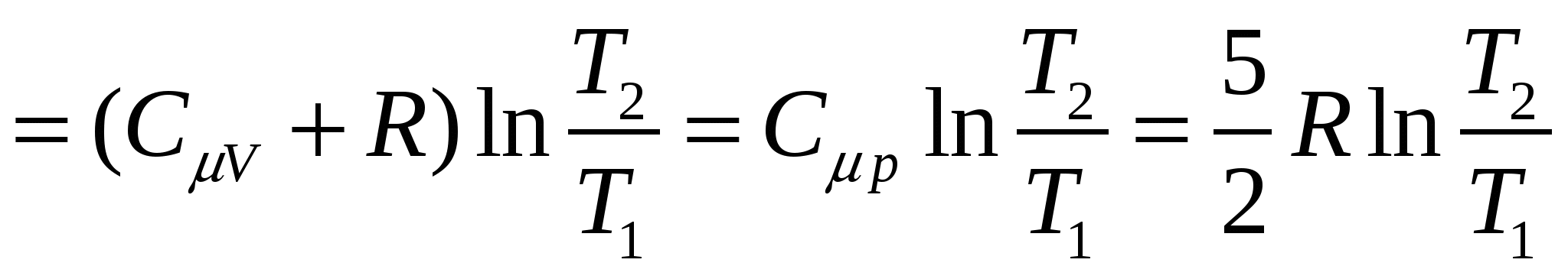 . (5.12.5) . (5.12.5)Здесь 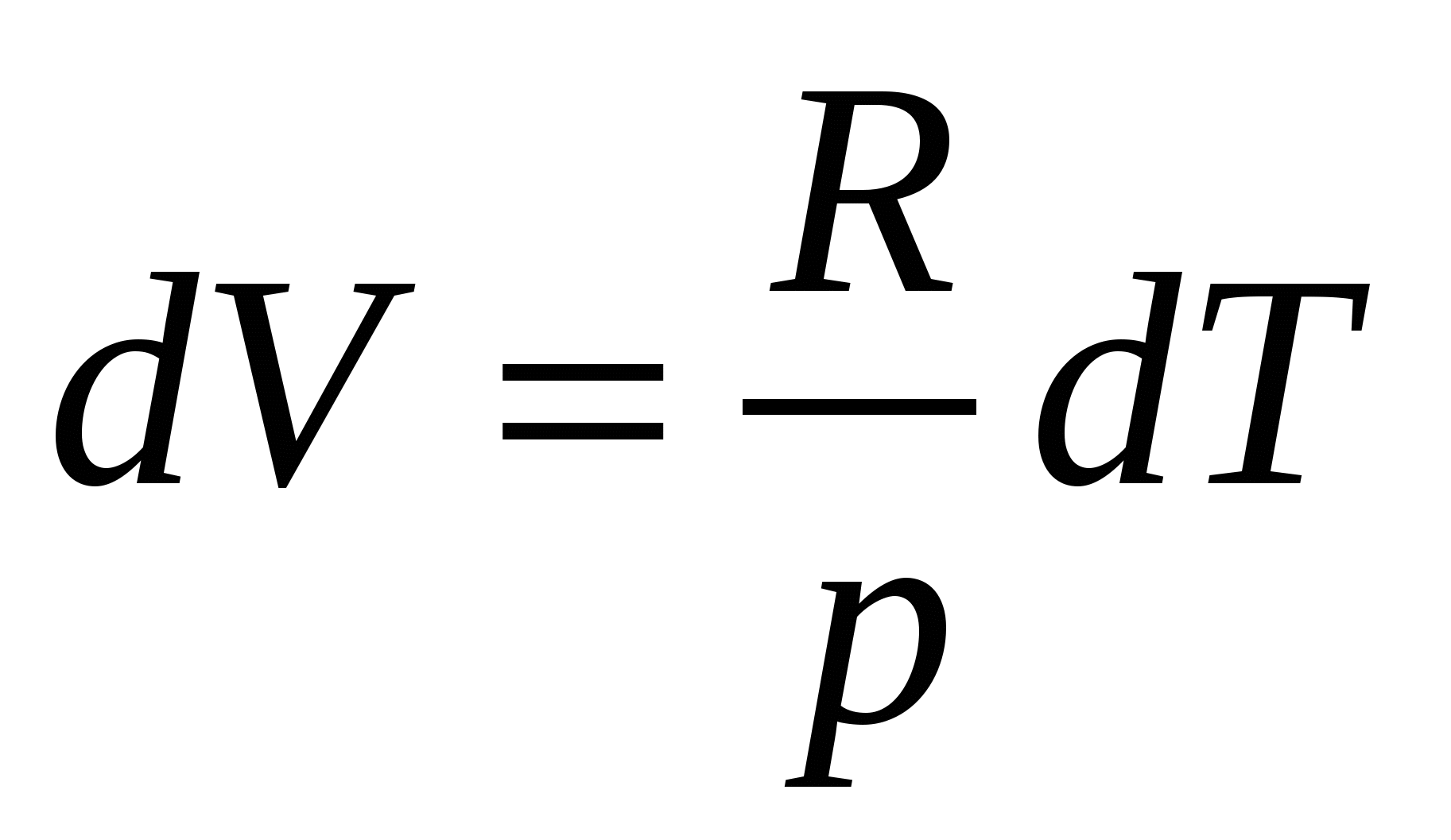 , ,которое получается для изобарного процесса из уравнения Клапейрона – Менделеева (5.12.2).
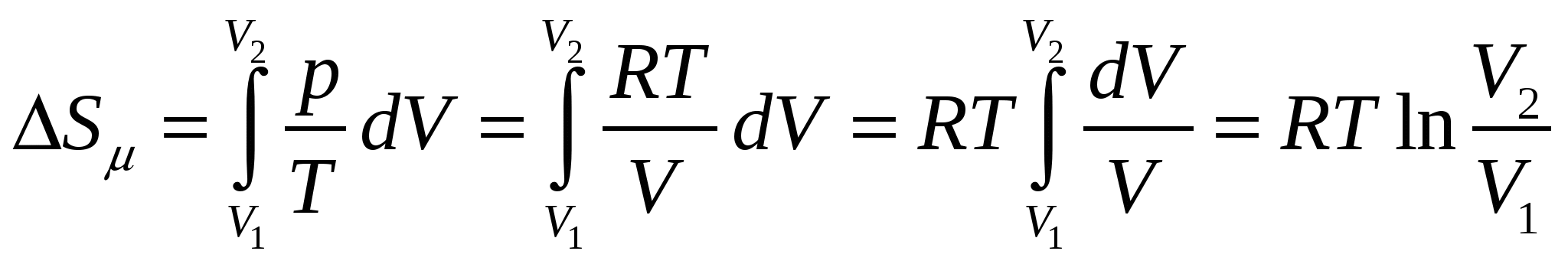 , (5.12.6) , (5.12.6)где Т - температура изотермического процесса и 4) Адиабатный процесс Ответ: 1) 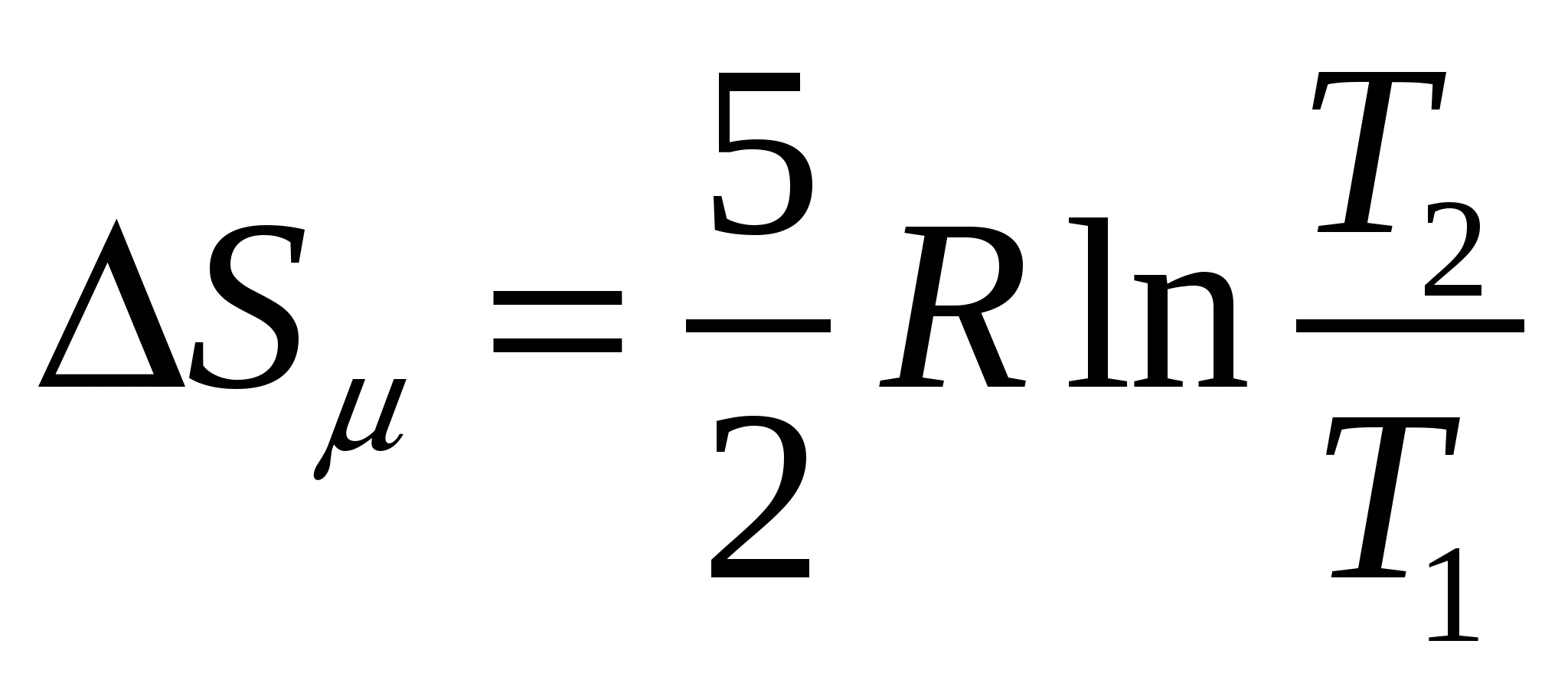 , 3) , 3) Задача №13 Определить изменение Решение Задача решается на основе формул для приращения энтропии молярной теплоты плавления и молярной теплоты испарения (парообразования) 1) Плавление происходит при постоянной температуре 2) Кипение происходит при постоянной температуре Оба процесса протекают при получении веществом теплоты извне, поэтому энтропия увеличивается. Ответ: 1) Задача №14 Два тела, имеющие массы m1 и m2, температуры Решение Начальное состояние тел не является равновесным, поскольку Расчеты выполняются на основе закона сохранения энергии и определения энтропии. Если температура тела 1 уменьшилась от которое пошло на увеличение, Из (5.14.1)и (5.14.2) следует, что равновесная температура двух тел Изменение энтропия тела 1 в случае обратимого охлаждения от 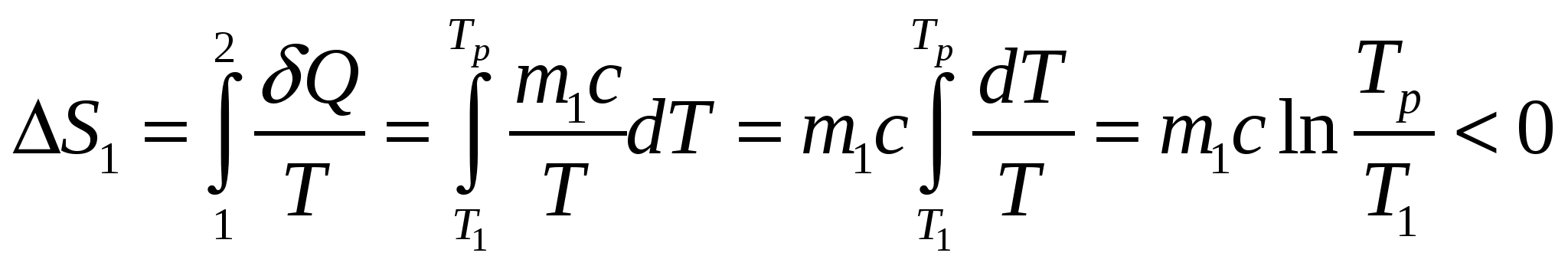 . (5.14.4) . (5.14.4)Изменение энтропия тела 2 в случае обратимого нагревания от 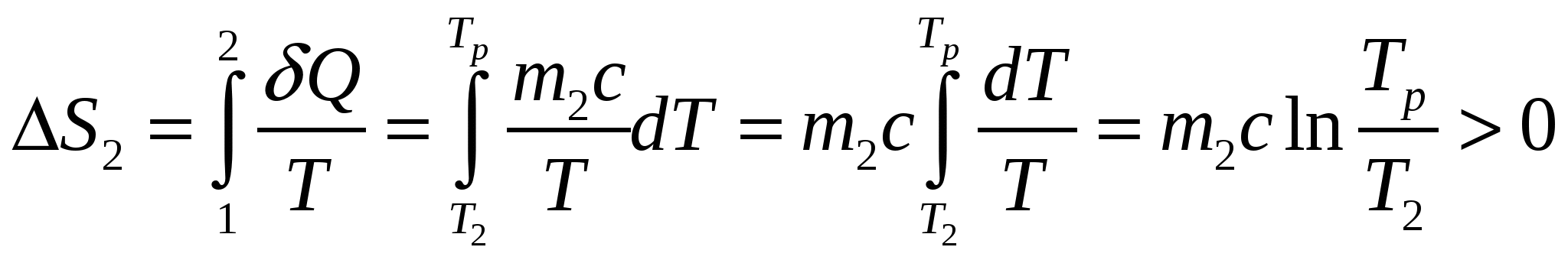 . (5.14.5) . (5.14.5)Полное изменение энтропии двух тел 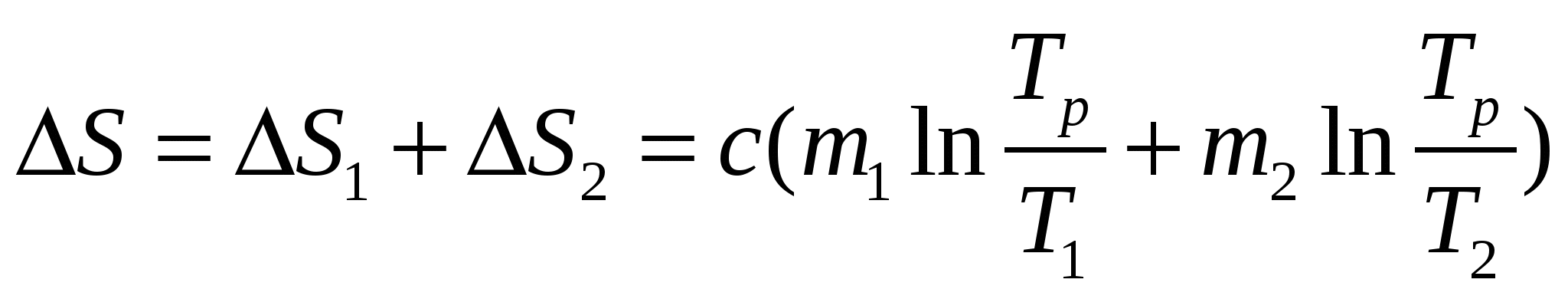 . (5.14.6) . (5.14.6)Поскольку в случае Ответ: 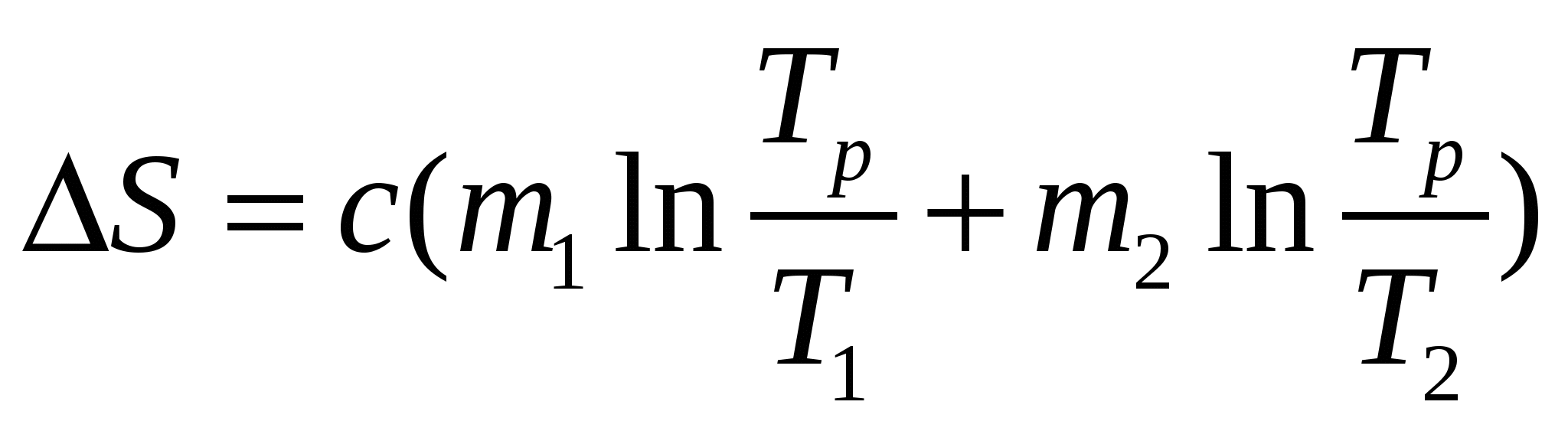 . .6. Процессы переноса В отсутствии внешнего силового поля равновесное состояние системы характеризуется постоянными по всему объему системы средними значениями концентрации частиц nи температуры Т. Если отклонения от равновесия невелики, можно ввести представление о локальном равновесии в малых макроскопических областях системы. Каждая такая область характеризуется своими величинами концентрации и температуры. Благодаря хаотическому тепловому движению частиц в неравновесной системе самопроизвольно (спонтанно) формируются процессы переноса вещества (диффузия) и внутренней энергии, зависящей от температуры (теплопроводность). Эти процессы переноса стремятся выравнить значения nи Т по всему объему системы и перевести систему в равновесное состояние. В задачах рассматриваются стационарные (не зависящие от времени) процессы диффузии и теплопроводности в идеальном газе. Допустим, что процессы переноса происходят только вдоль оси х. Диффузия описывается законом Фика где где В равновесном состоянии |

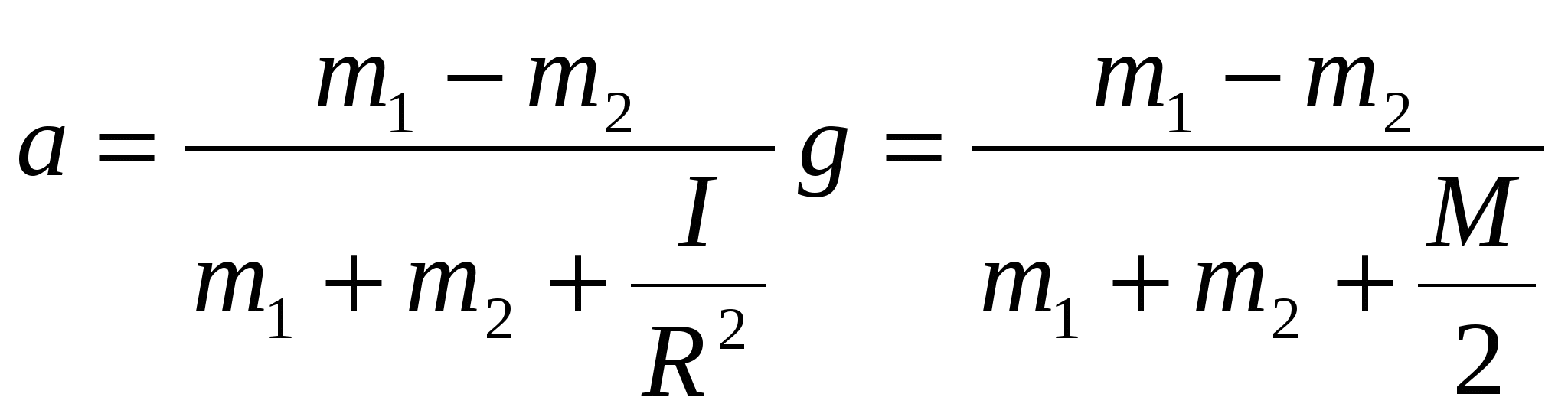 .
.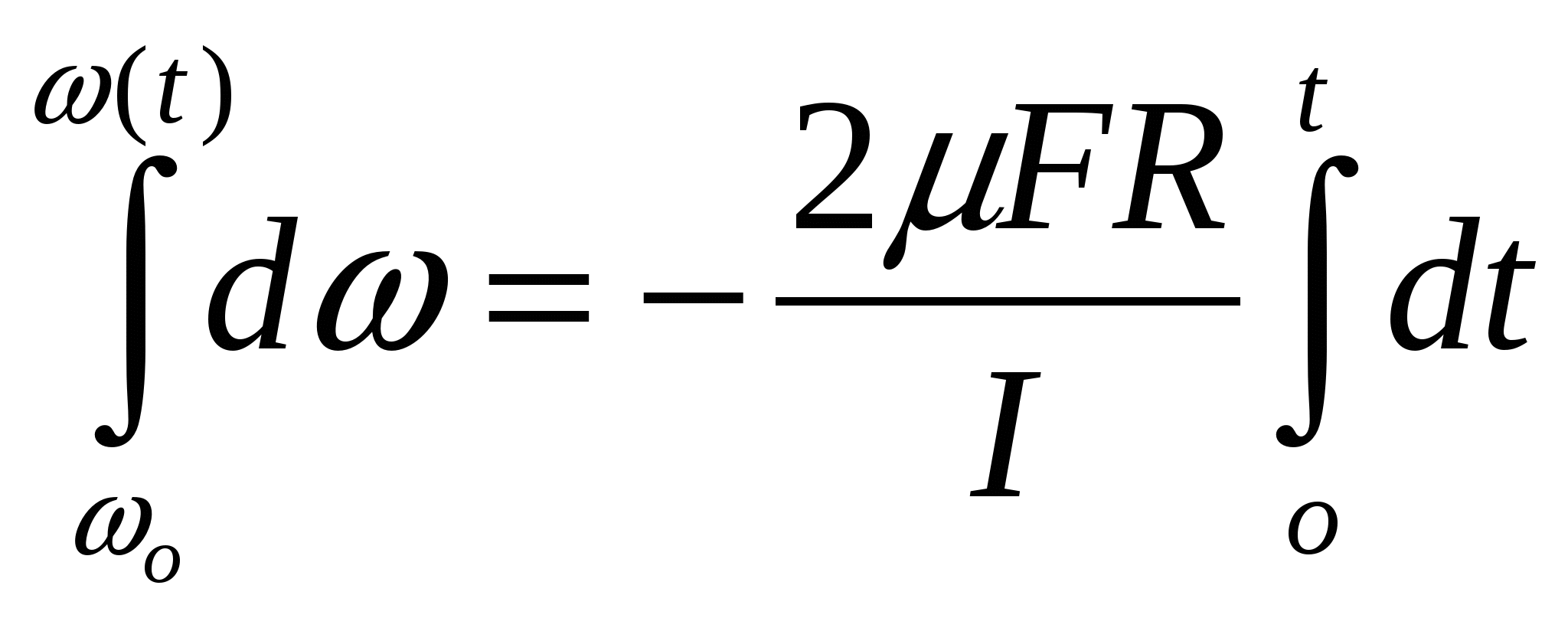
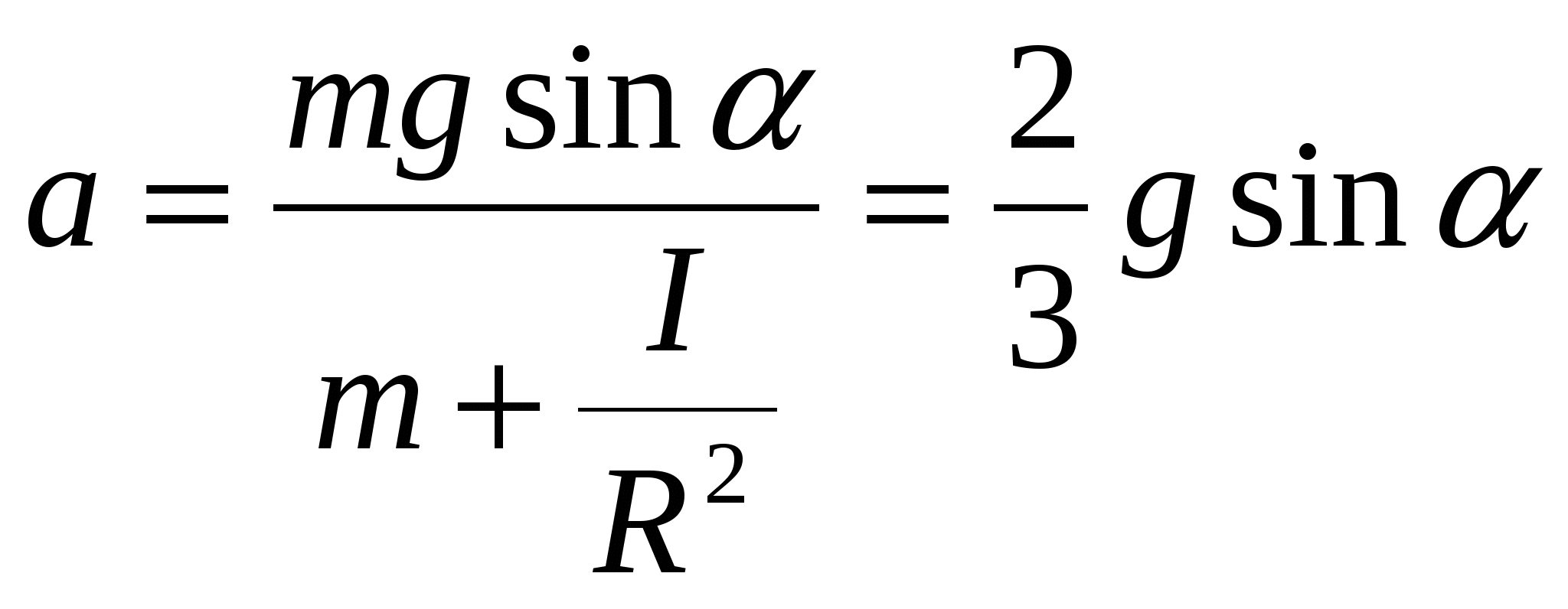 .
.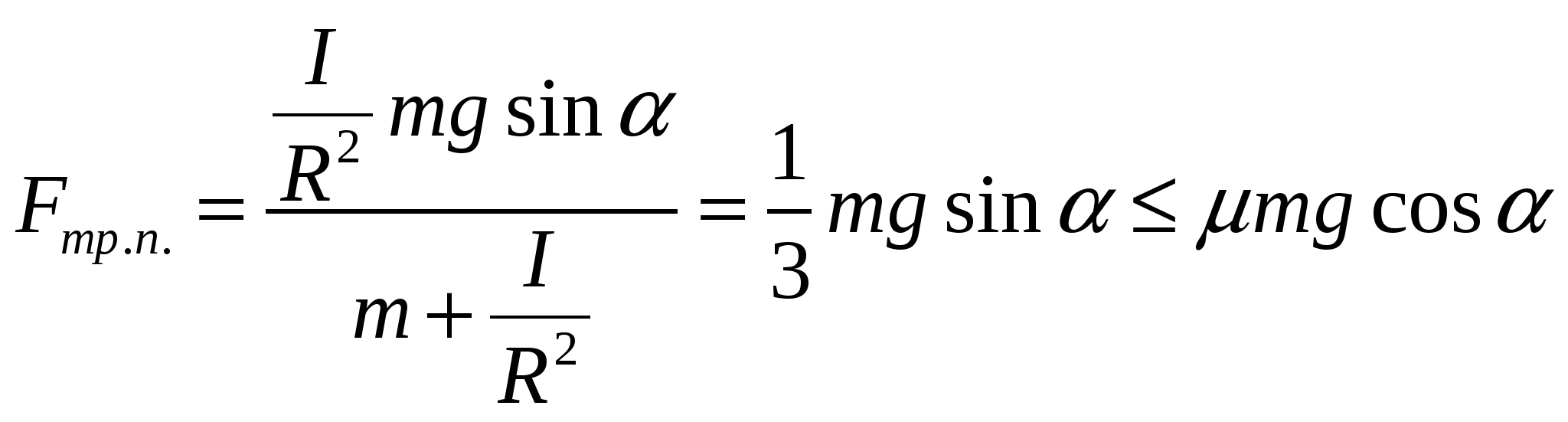 ,
,