Лабораторная работа № 3.5
ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА
МЕТОДОМ МАГНИТНОЙ ФОКУСИРОВКИ
Цель работы: 1) изучение движения заряженных частиц в электрическом и магнитном полях;
2) экспериментальное определение удельного заряда электрона.
Схема экспериментальной установки
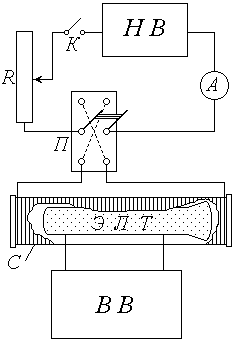
НВ – низковольтный выпрямитель;
К – ключ;
R – реостат;
А – амперметр;
П – переключатель;
С – соленоид;
ЭЛТ – электронно-лучевая трубка;
ВВ – высоковольтный выпрямитель
Описание установки и методики измерений
Экспериментальная установка включает в себя две электрические цепи. Источник питания первой цепи – низковольтный выпрямитель НВ – подает постоянное напряжение на соленоид С, предназначенный для создания однородного магнитного поля. Эта цепь замыкается и размыкается ключом К; реостат R служит для изменения силы тока в соленоиде, а амперметр А – для измерения этого тока. С помощью переключателя П можно изменять направление тока, а следовательно, и направление магнитного поля соленоида.
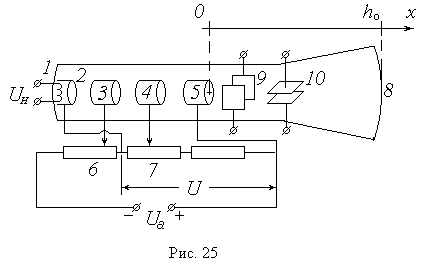
Основной частью второй электрической цепи и установки в целом является электронно-лучевая трубка ЭЛТ, размещенная внутри соленоида С и подключенная к источнику постоянного напряжения – высоковольтному выпрямителю ВВ. Электронно-лучевая трубка представляет собой стеклянный баллон, из которого откачан воздух. Упрощенная принципиальная электрическая схема ЭЛТ приведена на рис. 25.
Рис. 1
С одного из выходов выпрямителя ВВ снимается напряжение накала Uни подается на нагреватель 1. С поверхности разогретого им до высокой температуры катода 2 испускаются электроны (происходит явление термоэлектронной эмиссии). Высоковольтный выпрямитель подает на ЭЛТ высокое (порядка сотен вольт) анодное напряжение Uа ; при этом между катодом 2 и анодом 5 возникает ускоряющая разность потенциалов U. Под действием этой разности потенциалов электроны устремляются от катода к аноду и, пролетая сквозь него (анод имеет форму полого цилиндра), по инерции движутся дальше и попадают на экран 8. Экран покрыт флюоресцирующим веществом, благодаря чему на нем можно увидеть след электронного пучка. Модулятор 3 и первый анод 4, также выполненные в виде полых цилиндров, служат для регулирования яркости и фокусировки пучка (подаваемый на модулятор отрицательный потенциал можно изменять с помощью потенциометра 6, а положительный потенциал первого анода – с помощью потенциометра 7). Вертикальные (9) и горизонтальные (10) пары пластин предназначены для отклонения электронного пучка соответственно в горизонтальном и вертикальном направлениях (в данной работе эти пластины не используются).
Рассмотрим превращение энергии одного из электронов на пути от катода к аноду. Вылетая из катода, электрон имеет начальную скорость 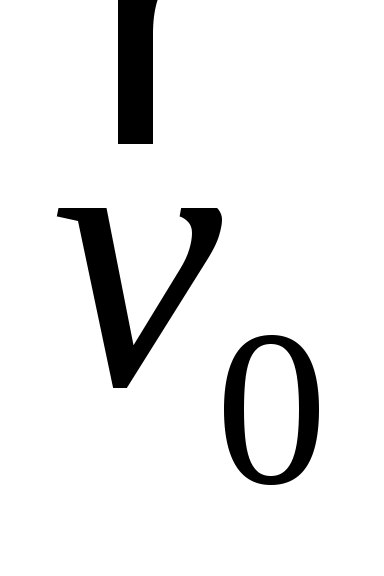 (направление и величина этой скорости у разных электронов различны) и следовательно, обладает некоторой начальной кинетической энергией Wk0 = mv02/2, где m – масса электрона. Попадая в электрическое поле, он приобретает также потенциальную энергию Wp0 = -e k , которая по достижении им анода становится равной Wp = -eа (здесь е – элементарный электрический заряд; k и а – потенциалы катода и анода соответственно). Пройдя ускоряющую разность потенциалов, электрон увеличивает свою кинетическую энергию до значения Wk = mv2/2, где (направление и величина этой скорости у разных электронов различны) и следовательно, обладает некоторой начальной кинетической энергией Wk0 = mv02/2, где m – масса электрона. Попадая в электрическое поле, он приобретает также потенциальную энергию Wp0 = -e k , которая по достижении им анода становится равной Wp = -eа (здесь е – элементарный электрический заряд; k и а – потенциалы катода и анода соответственно). Пройдя ускоряющую разность потенциалов, электрон увеличивает свою кинетическую энергию до значения Wk = mv2/2, где 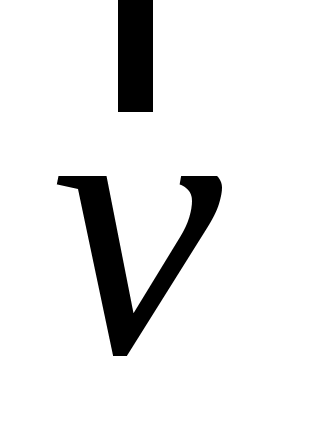 – его скорость на выходе из анода. Записав уравнение закона сохранения энергии – его скорость на выходе из анода. Записав уравнение закона сохранения энергии
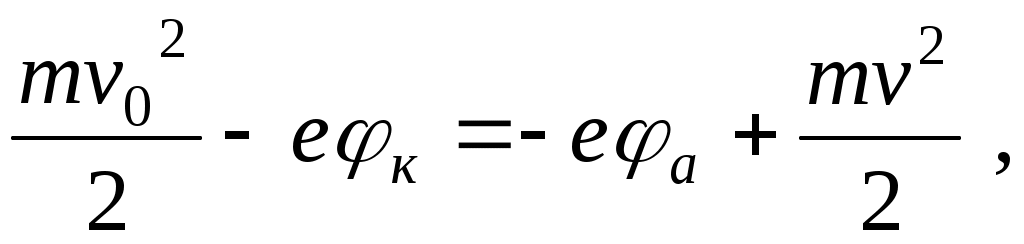
найдем конечную скорость электрона:
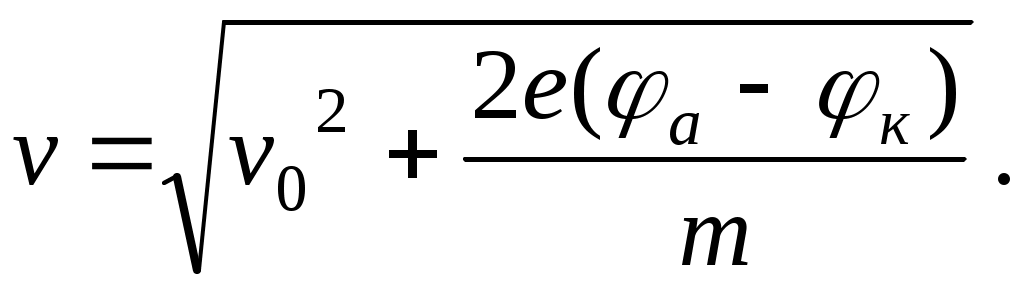 (1) (1)
Как видно из схемы ЭЛТ (рис. 1), потенциалы катода и анода связаны соотношением a = k + U. Скорость электрона при вылете из катода значительно меньше скорости, приобретаемой им после прохождения ускоряющей разности потенциалов: v0 << v. С учетом этого выражение (1) будет иметь вид
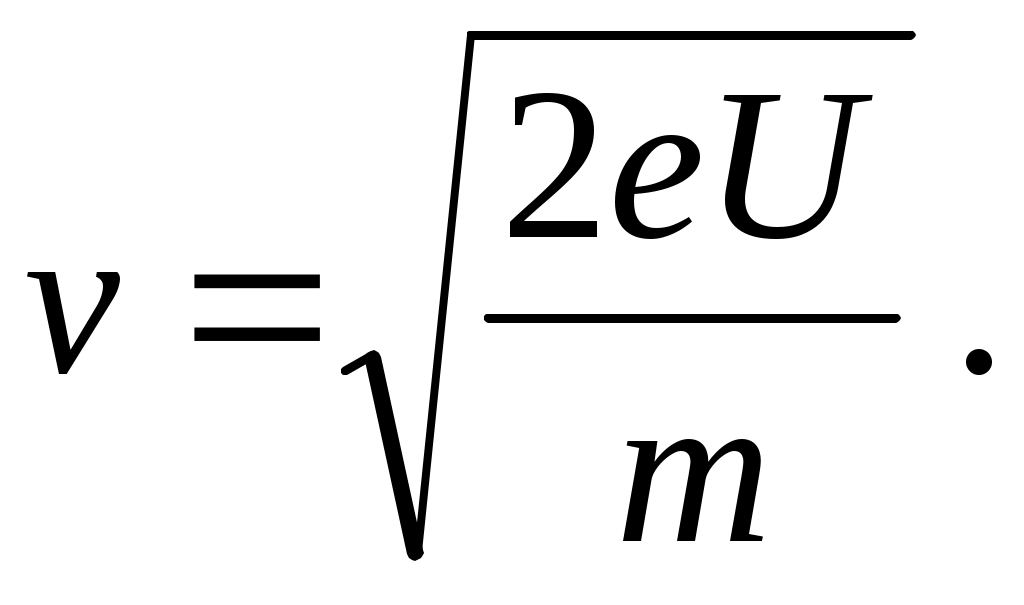 (2) (2)
С помощью модулятора 3 и первого анода 4 невозможно добиться идеальной фокусировки электронного пучка. Поэтому на выходе из анода 5 пучок расходится под некоторым малым углом, и на экране наблюдается пятно сравнительно большого размера равномерной яркости (из-за наличия отклоняющих пластин 9 и 10 это пятно имеет прямоугольную форму).
Н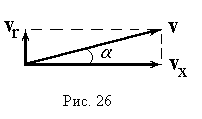
Рис. 2
аправим ось Ох вдоль оси ЭЛТ в сторону экрана 8, а начало координат совместим с точкой выхода электронов из анода (рис. 1). Расстояние от анода до экрана h0 является конструктивным параметром трубки, т.е. постоянной для данной установки величиной. Как уже отмечалось, это расстояние в отсутствие внешних воздействий электрон пролетает по инерции – с постоянной по величине и направлению скоростью 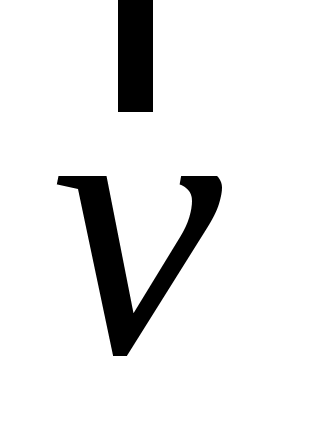 . Так как электронный пучок расходится под некоторым углом, вектор скорости имеет не только осевую составляющую . Так как электронный пучок расходится под некоторым углом, вектор скорости имеет не только осевую составляющую 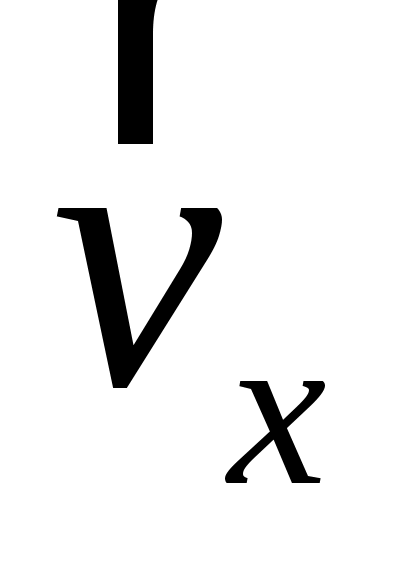 , но и радиальную (перпендикулярную оси трубки) , но и радиальную (перпендикулярную оси трубки) 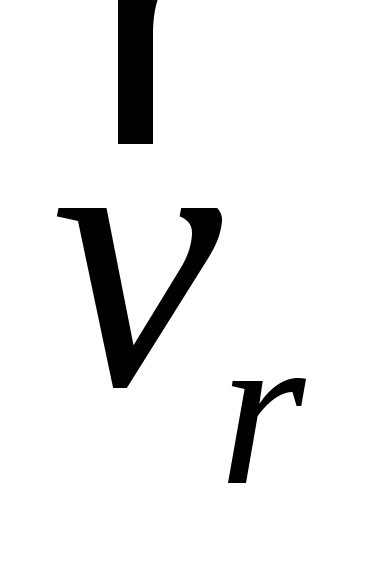 , причем у разных электронов величина и направление , причем у разных электронов величина и направление 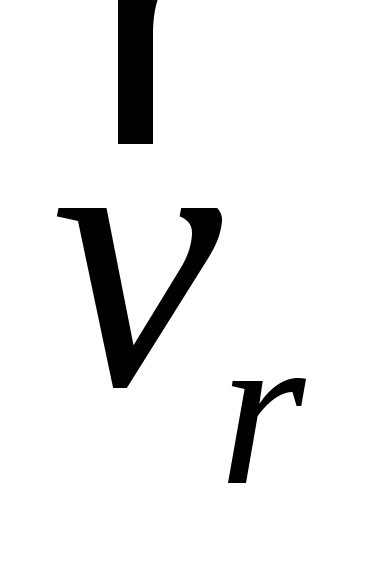 (в плоскости yOz) различны. При малых углах отклонения (рис. 2) составляющая (в плоскости yOz) различны. При малых углах отклонения (рис. 2) составляющая 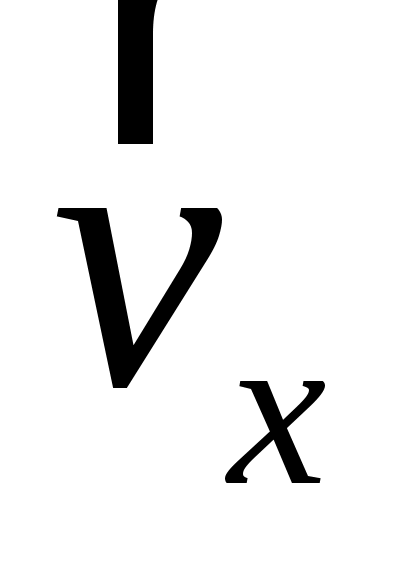 во много раз превосходит по модулю составляющую во много раз превосходит по модулю составляющую 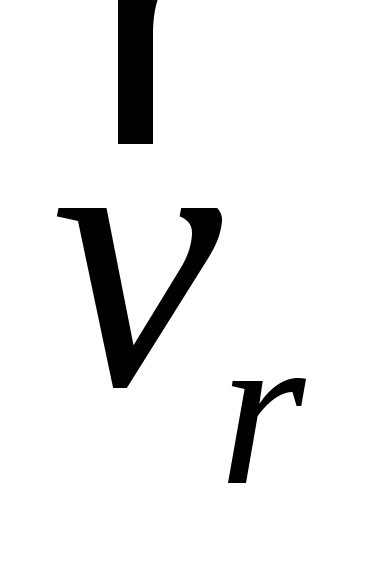 . При этом с достаточной степенью точности можно положить . При этом с достаточной степенью точности можно положить
vx v. (3)
Таким образом, осевая составляющая скорости vx у всех электронов практически одинакова и может быть найдена по формуле (2).
При замыкании ключа К по виткам соленоида С течет постоянный ток силой I, создающий внутри соленоида, а следовательно, и внутри ЭЛТ постоянное магнитное поле напряженностью
H = In, (4)
где n – число витков на единицу длины соленоида. Индукция магнитного поля соленоида 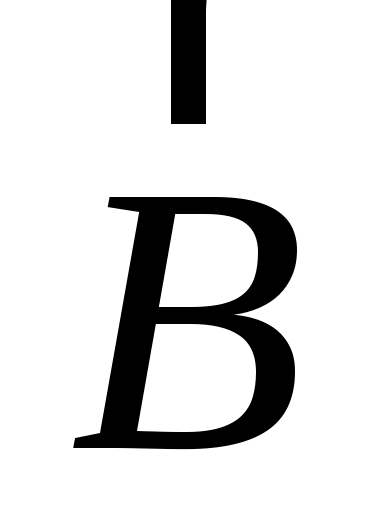 направлена вдоль его оси, совпадающей с осью трубки и выбранной нами осью Ох. Так как среда внутри ЭЛТ представляет собой вакуум, индукция направлена вдоль его оси, совпадающей с осью трубки и выбранной нами осью Ох. Так как среда внутри ЭЛТ представляет собой вакуум, индукция 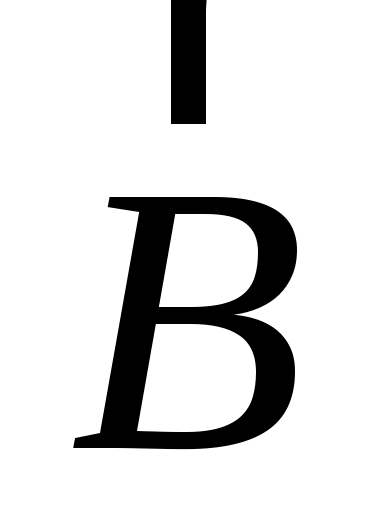 связана с напряженностью связана с напряженностью 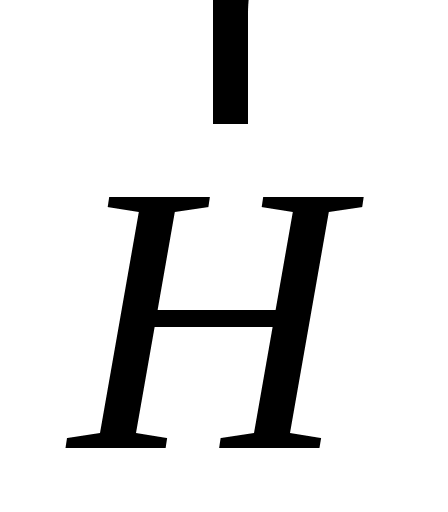 соотношением соотношением 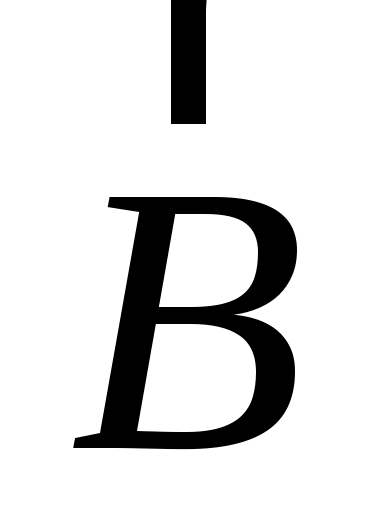 = 0 = 0 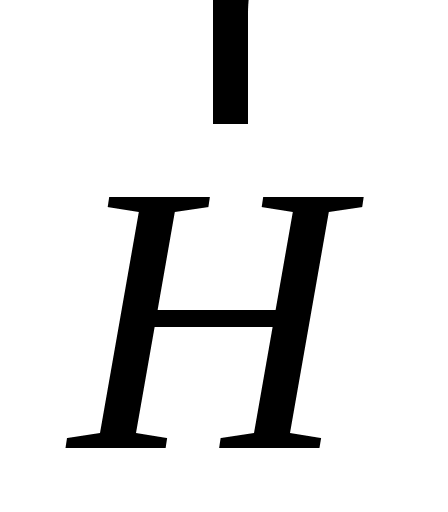 , где 0 – магнитная постоянная. С учетом (4) модуль вектора , где 0 – магнитная постоянная. С учетом (4) модуль вектора 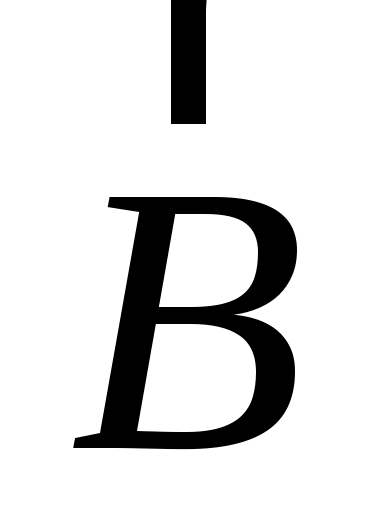 равен равен
B = 0 In. (5)
В магнитном поле на летящий со скоростью v электрон действует сила Лоренца
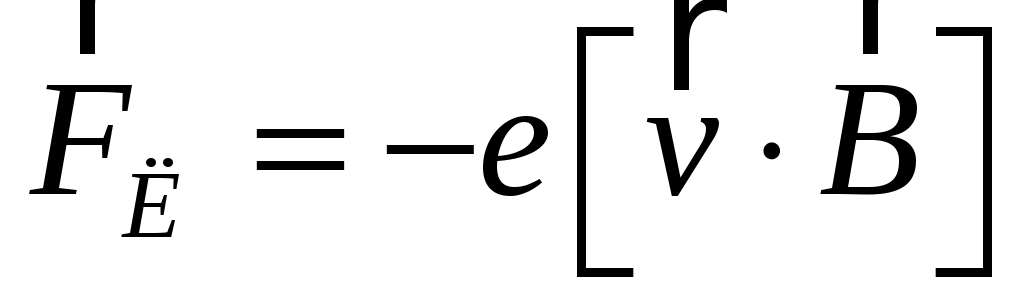 , (6) , (6)
модуль которой равен
Fл = evBsin,
где – угол, который вектор скорости 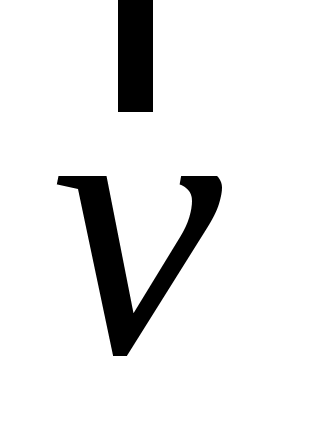 составляет с направлением поля, т.е. с осью Ох . Как видно из рис. 26, vsin= vr . Таким образом, составляет с направлением поля, т.е. с осью Ох . Как видно из рис. 26, vsin= vr . Таким образом,
Fл = evrB.
Из (6) следует, что вектор  направлен перпендикулярно вектору направлен перпендикулярно вектору 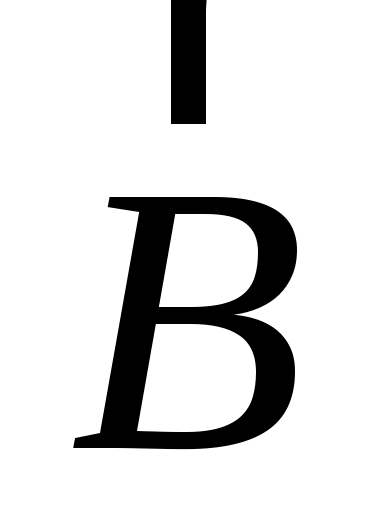 , – следовательно, лежит в плоскости yOz; кроме того, он перпендикулярен вектору , – следовательно, лежит в плоскости yOz; кроме того, он перпендикулярен вектору 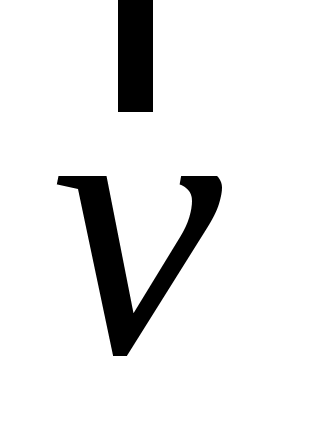 , а значит, и его проекции , а значит, и его проекции 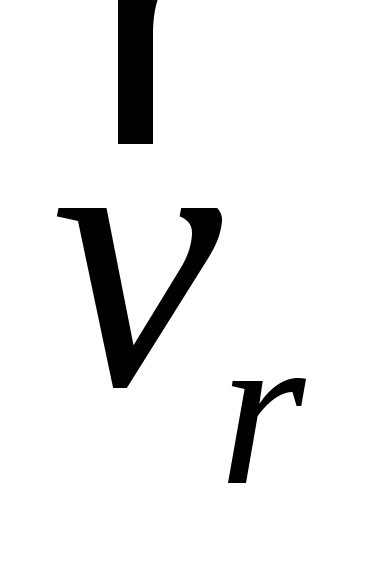 . Поэтому сила Лоренца не может изменить величину скорости электрона, и модули векторов . Поэтому сила Лоренца не может изменить величину скорости электрона, и модули векторов 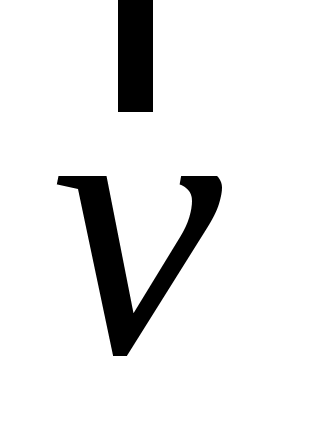 = v, = v, 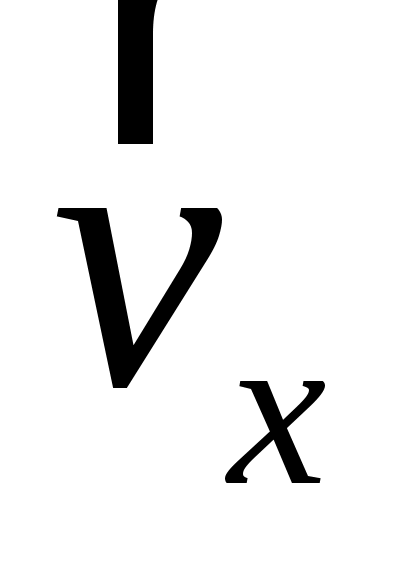 = vx и = vx и 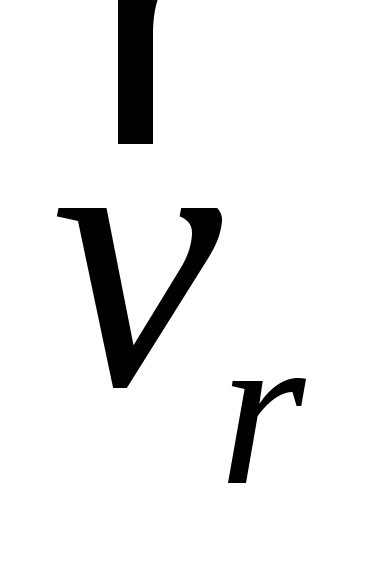 = vr остаются постоянными. В то же время, согласно второму закону Ньютона, сила = vr остаются постоянными. В то же время, согласно второму закону Ньютона, сила 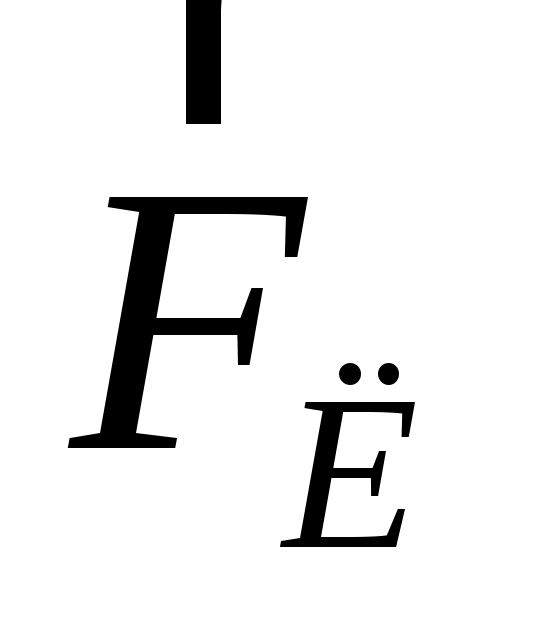 сообщает электрону ускорение сообщает электрону ускорение 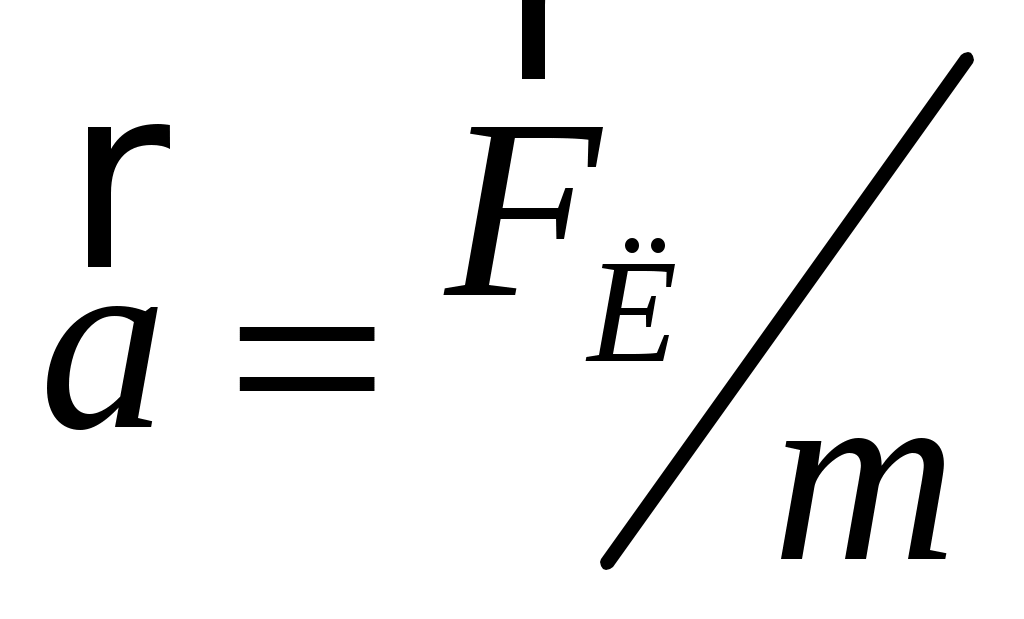 , по модулю равное , по модулю равное
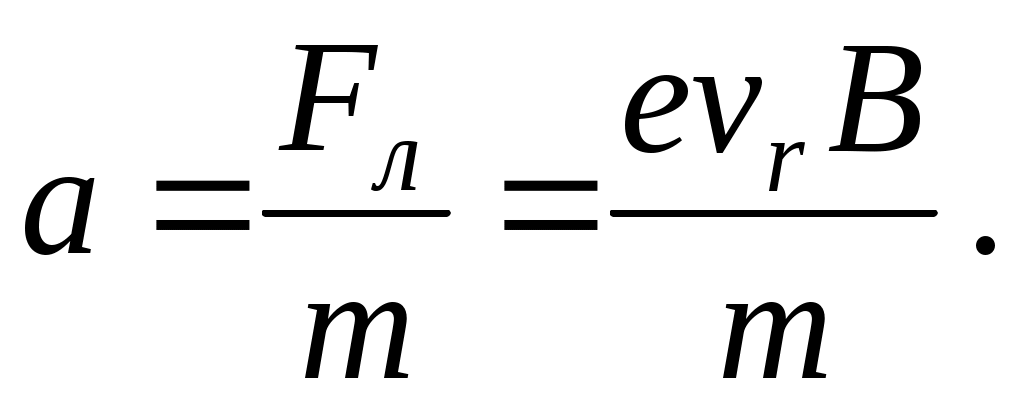 (7) (7)
Будучи перпендикулярным скорости, это ускорение является нормальным. При неизменных значениях vr и В имеем a = an=const, в то время как тангенциальная составляющая ускорения a = 0. Это означает, что в проекции на плоскость yOz траектория движения электрона представляет собой окружность. Вдоль оси Ох электрон продолжает двигаться по инерции с постоянной скоростью vх. Результирующей траекторией является пространственная кривая – винтовая линия. Эта линия характеризуется двумя параметрами: радиусом витка (окружности в плоскости yOz) R и шагом h – расстоянием, на которое электрон перемещается вдоль оси Ох за время одного полного оборота по окружности (т.е. за период обращения Т).
Для определения радиуса витка воспользуемся выражением (7). Учитывая, что нормальное (центростремительное) ускорение связано со скоростью движения по окружности vr известным соотношением
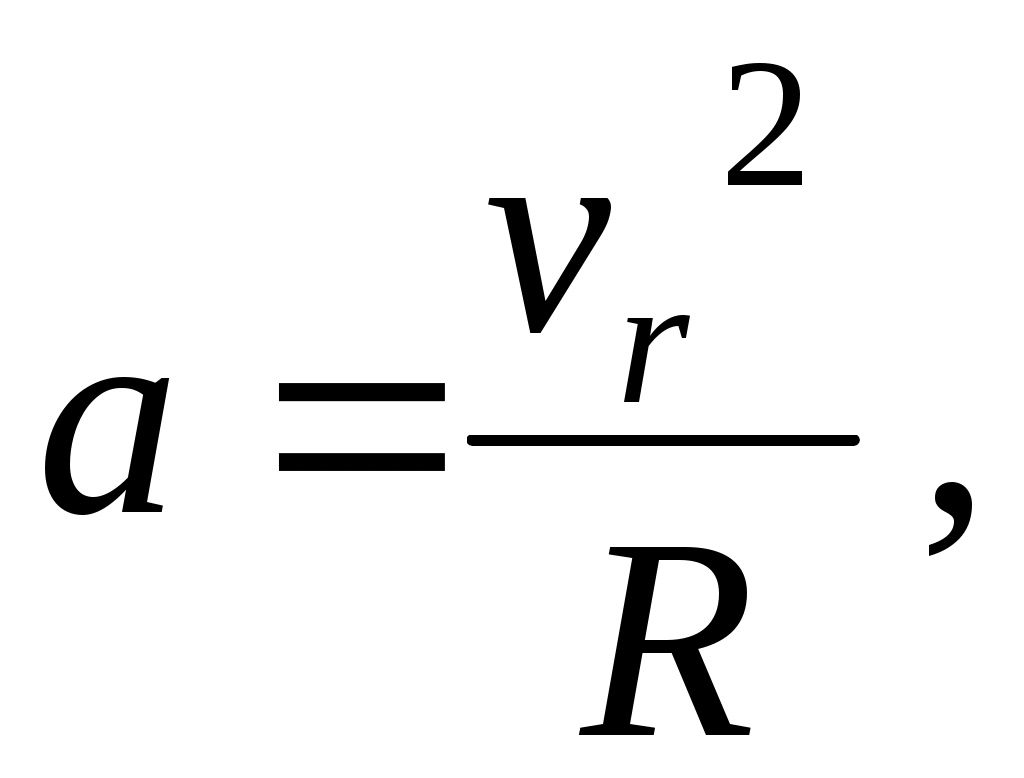
имеем:
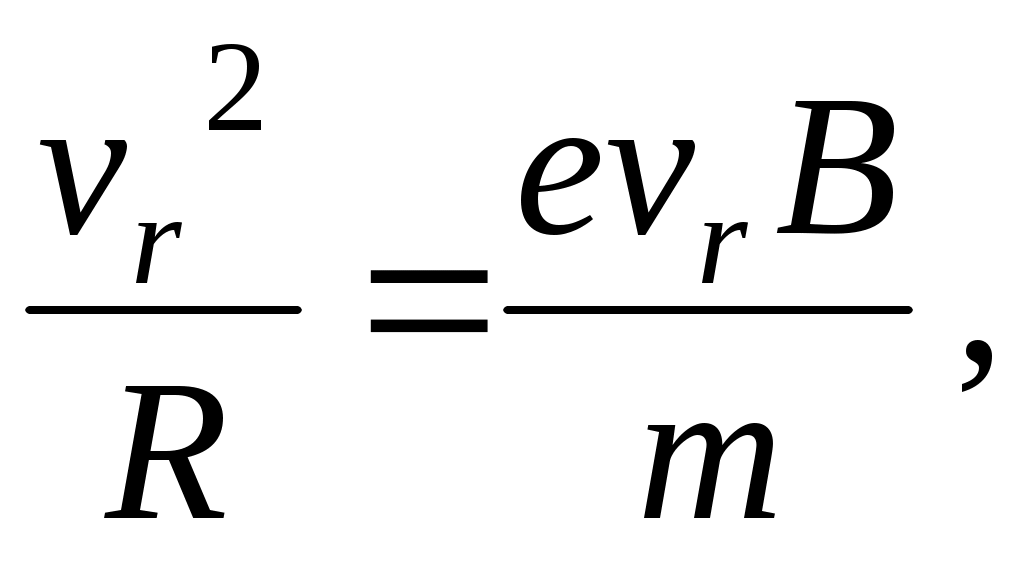
откуда
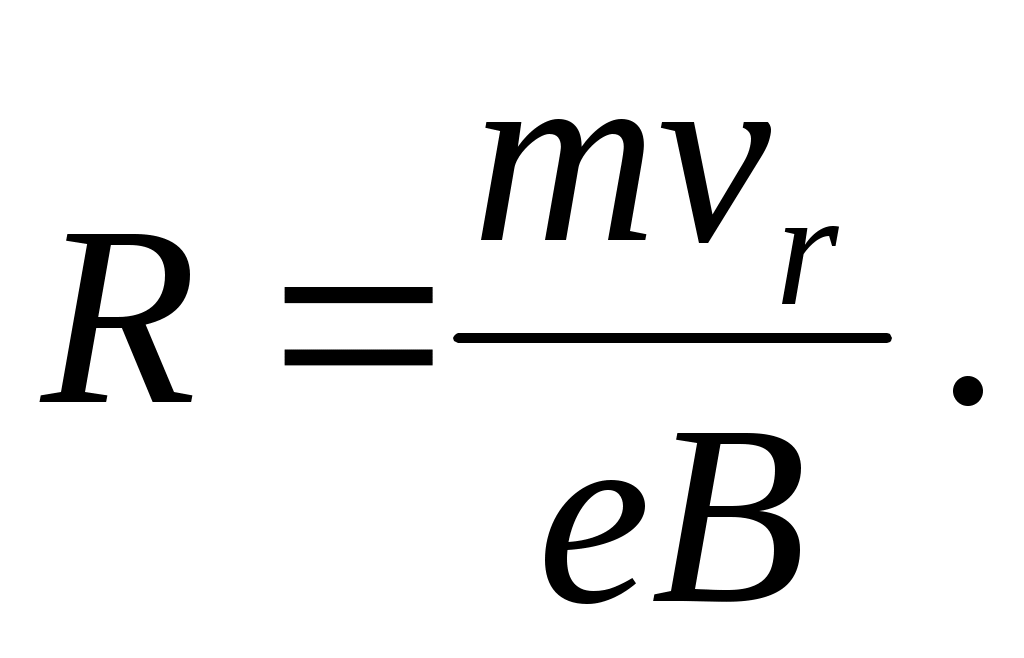 (8) (8)
Период обращения по окружности витка равен
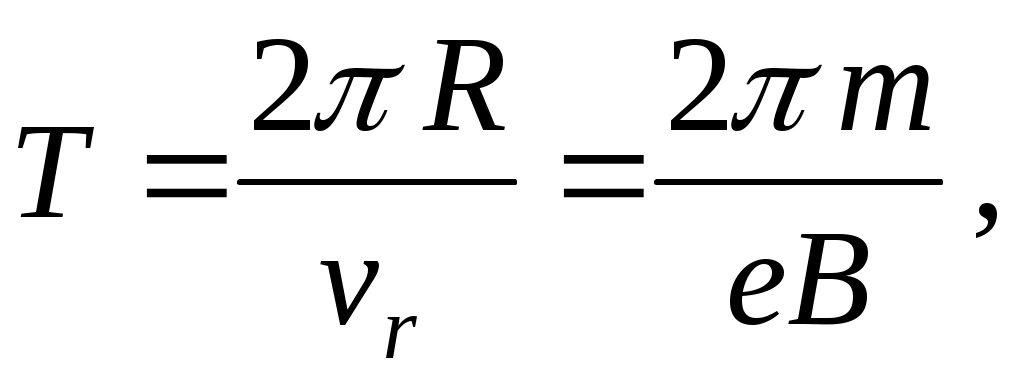 (9) (9)
а шаг винтовой линии h = vr T ; с учетом (3) и (9) имеем
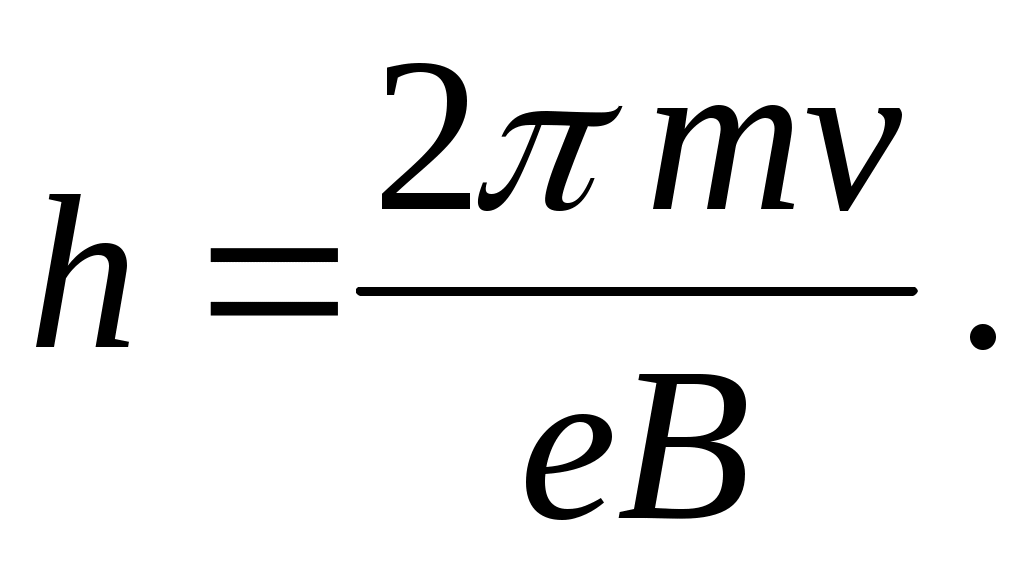 (10) (10)
Из выражений (2), (8)-(10) можно сделать вывод о том, что электроны, имеющие различные по величине и направлению начальные скорости, движутся в магнитном поле по окружностям разного радиуса, однако период обращения и шаг винтовой линии у всех электронов практически одинаковы. Таким образом, вылетевшие из начала координат (на выходе из анода) электроны спустя промежуток времени Т почти одновременно пересекают ось Ох в одной точке с координатой x = h. При определенных значениях скорости v и магнитной индукции В можно добиться того, что эта точка будет расположена на экране ЭЛТ, т.е. будет иметь место равенство h = h0 . При постоянной скорости v сфокусировать электронный пучок на экране можно путем подбора величины В – в этом и заключается метод магнитной фокусировки (метод Буша).
Рис. 3-5 иллюстрируют этот метод, «прослеживая» траектории трех электронов, имеющих разные по величине и направлению радиальные составляющие скорости 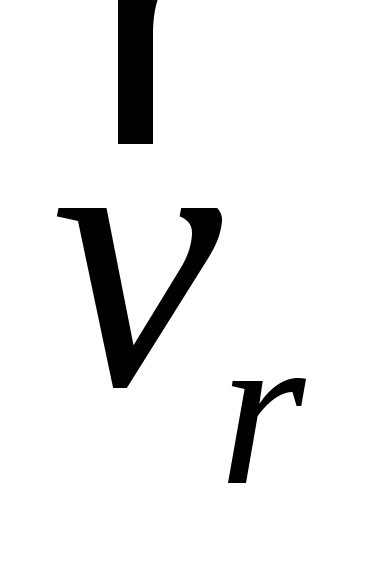 1 , 1 , 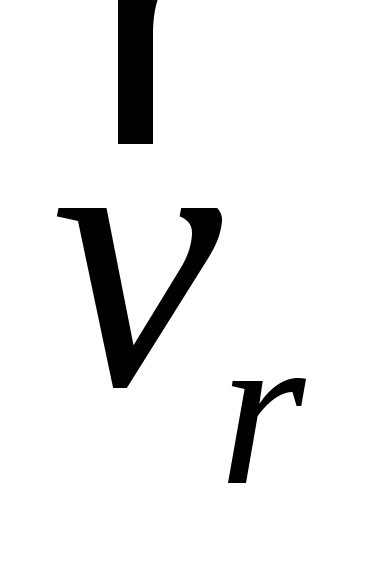 2 и 2 и 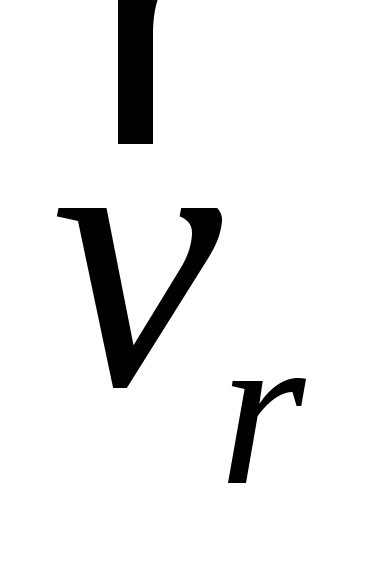 3 . 3 .
При малых значениях магнитной индукции В шаг винтовой линии h больше расстояния от анода до экранаh0 , и электроны не успевают совершить полный оборот по окружности. Попадая на экран, они оставляют на нем размытый след (рис. 3).
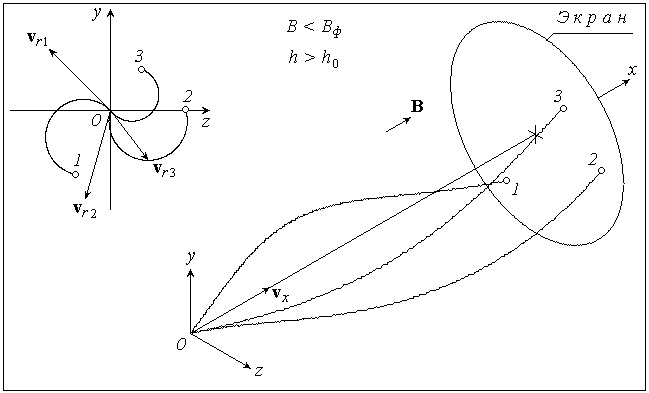
Рис. 3
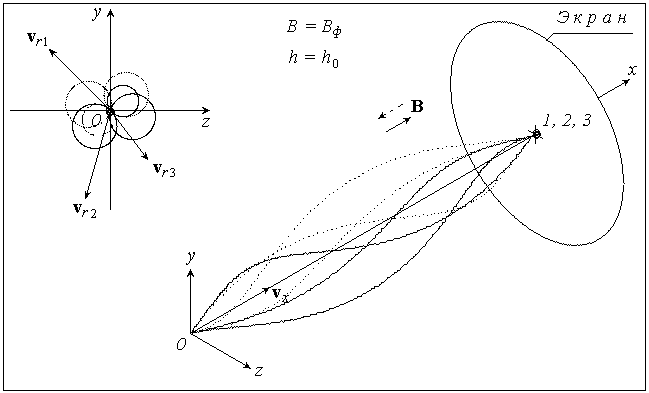
Рис. 4
При некотором значении магнитной индукции В = Вф время движения электронов от анода к экрану равно периоду обращения; при этом h = h0 , и электронный пучок фокусируется в одну точку на экране (на рис. 4 этот случай показан при двух возможных направлениях вектора 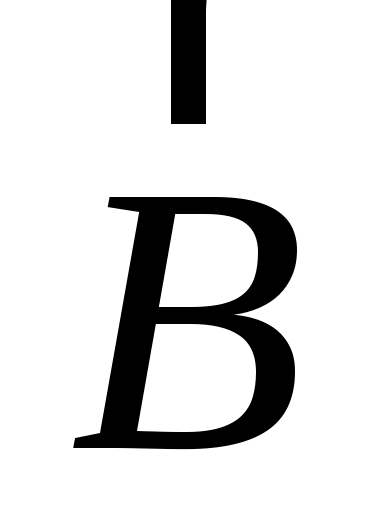 , т.е. при противоположных направлениях тока в соленоиде). , т.е. при противоположных направлениях тока в соленоиде).
Дальнейшее увеличение магнитной индукции приводит к тому, что электроны «сходятся» в точке на оси Ох , еще не достигнув экрана (h < h0 ), а затем вновь «расходятся», оставляя на экране размытый след (рис. 5).
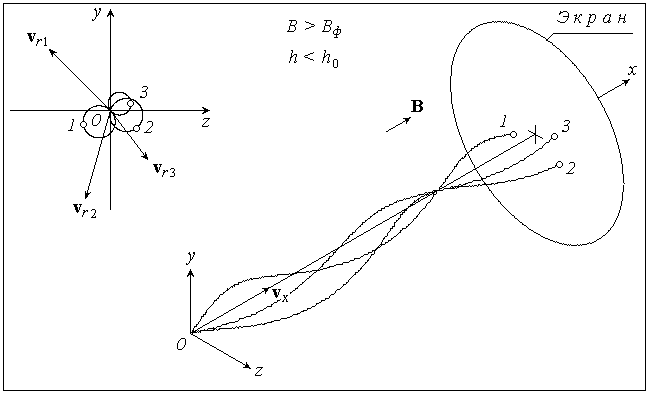
Рис. 5
Подставляя в (10) выражения для скорости (2) и для магнитной индукции (5), получим
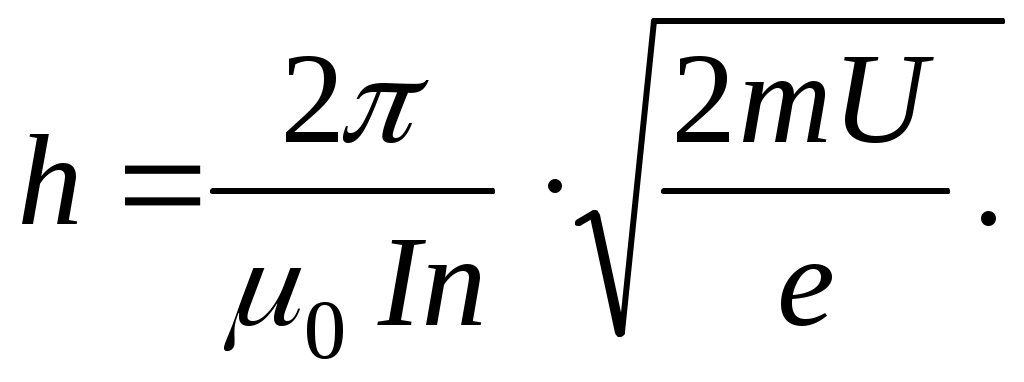 (11) (11)
Отношение заряда частицы к ее массе называется удельным зарядом. Для электрона эта величина равна по модулю e/m. Метод Буша позволяет экспериментально найти удельный заряд электрона на основе полученной выше формулы (11). Положив в ней h = h0 , выразим e/m:
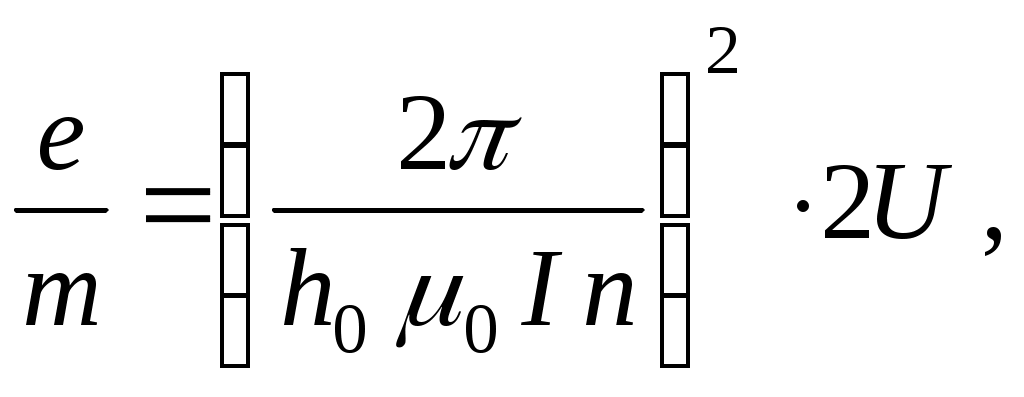 (12) (12)
где I – значение силы тока в соленоиде, при котором электронный пучок фокусируется в точку на экране.
Как отмечалось выше, расстояние h0 является конструктивным параметром ЭЛТ. В свою очередь, число витков на единицу длины n – конструктивный параметр соленоида. Зная эти параметры установки, измерив ускоряющую разность потенциалов U и «фокусирующий» ток I , по формуле (12) можно рассчитать удельный заряд электрона. Для получения более надежного результата следует повторить измерения при разных направлениях тока и различных значениях напряжения U . При этом величины h0 , n и 0 остаются постоянными, так что расчетную формулу удобно представить в виде
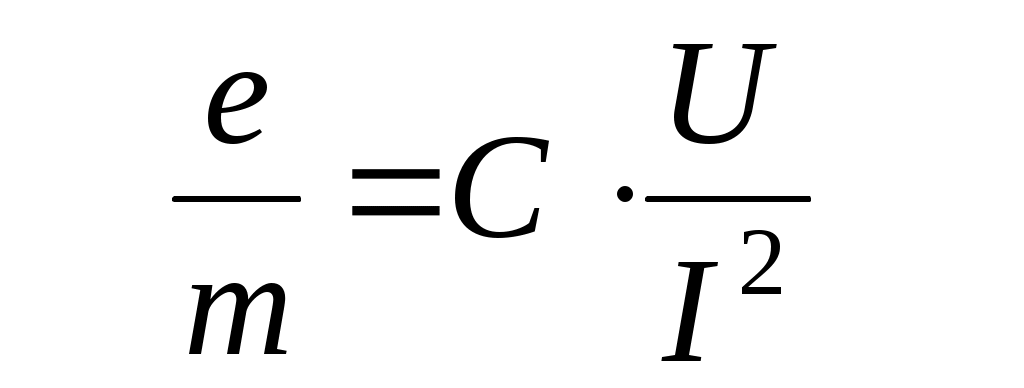 , (13) , (13)
где
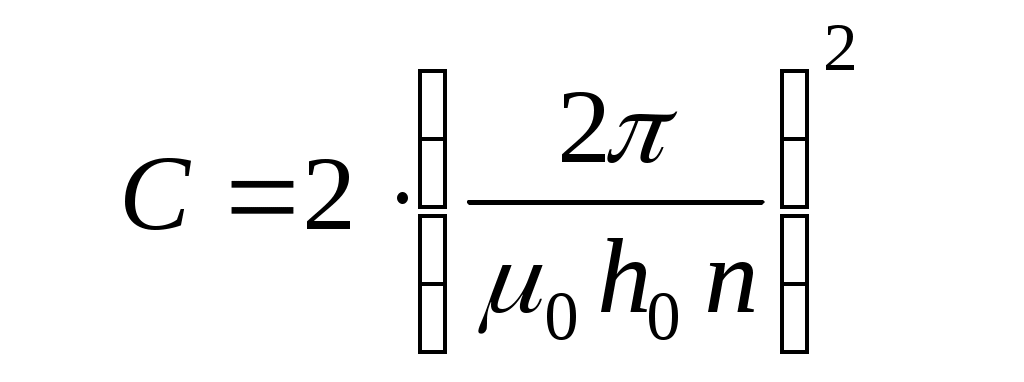 . (14) . (14)
Порядок измерений и обработки результатов
1. Ознакомьтесь с лабораторной установкой и рекомендациями к работе. Запишите в тетрадь величину h0 , а также диаметр d проволоки, из которой изготовлена обмотка соленоида (в метрах). Исходя из того, что провод намотан на катушку в один слой и его витки плотно прилегают друг к другу, определите число витков на единицу длины соленоида n (в м –1 ). Рассчитайте по формуле (14) значение константы С (в м2/Гн2 ) и запишите его в тетрадь.
2. Определите предел измерения, цену деления и класс точности амперметра и вольтметра (последний вмонтирован в панель высоковольтного выпрямителя ВВ). Научитесь снимать показания этих приборов и оцените абсолютные приборные погрешности измерения силы тока в соленоиде I и ускоряющей разности потенциалов U. Результаты соответствующих расчетов запишите в тетрадь.
3. Занесите в таблицу рекомендуемые значения U.
Номер опыта
|
U,
B
|
I1 ,
A
|
I2 ,
A
|
I ,
A
|
e/m,
ГКл/кг
|
(e/m),
ГКл/кг
|
[(e/m)]2,
(ГКл/кг)2
|
1
|
|
|
|
|
|
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
5
|
|
|
|
|
|
|
|
|
|
|
|
=
|
|
=
|
|
4. Под руководством преподавателя или лаборанта включите в сеть высоковольтный выпрямитель ВВ. Установите с помощью ручек потенциометра заданное начальное значение напряжения U. Убедитесь в исправности высоковольтной цепи (на экране ЭЛТ должно появиться размытое светящееся пятно прямоугольной формы).
5. Проследив за тем, чтобы реостат R был введен полностью, а ключ К – разомкнут, включите в сеть низковольтный выпрямитель НВ. Замкните ключ К.
6. Перемещая движок реостата R, наблюдайте за экраном ЭЛТ. Запишите в таблицу значение силы тока I 1 , при котором след электронного пучка на экране сходится в яркую точку. Уменьшив ток с помощью реостата до минимума, переключателем П измените направление тока. Вновь добившись фокусировки пучка, запишите в таблицу соответствующее значение силы тока I 2 .
7. Изменяя величину напряжения U, повторите п. 6 еще четыре раза. По окончании измерений уменьшите до минимума ток в низковольтной цепи и напряжение в высоковольтной. Отключите оба выпрямителя от сети.
8. Для каждого из проделанных опытов рассчитайте и занесите в таблицу среднее значение «фокусирующего» тока I =(I 1 + I 2 ) / 2. По формуле (13) вычислите удельный заряд электрона e/m. Переведите полученный результат в ГКл/кг и запишите его в таблицу.
9. Рассчитайте сумму найденных значений e/m и определите среднее значение 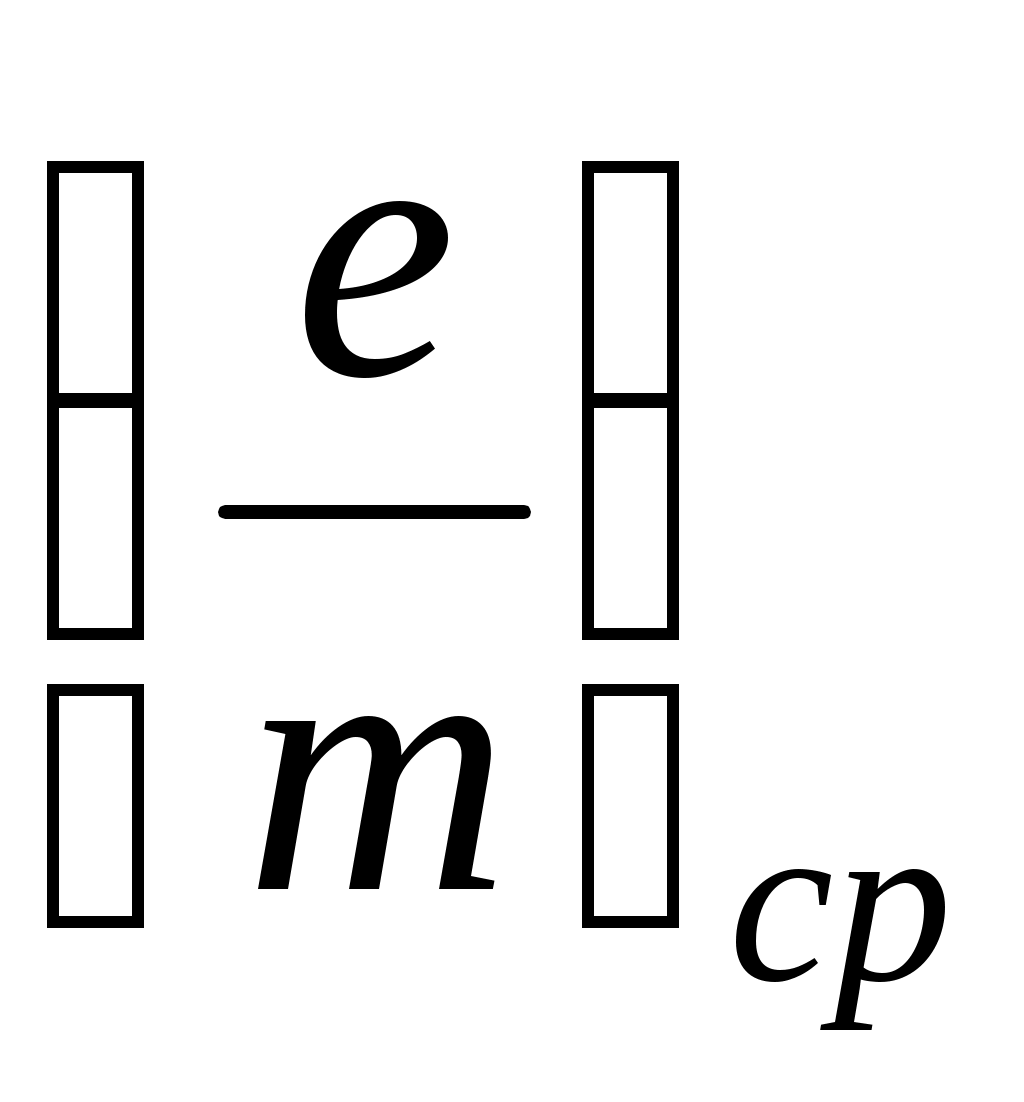 . .
10*. Выполните все расчеты, необходимые для оценки случайной погрешности измерения удельного заряда электрона s(e/m). Найдите величину s(e/m), задаваясь доверительной вероятностью = 0,95.
11*. Оцените относительные приборные погрешности прямых измерений силы тока EI и напряжения EU , а также абсолютную приборную погрешность косвенного измерения величины e/m. При необходимости используйте для этого формулу
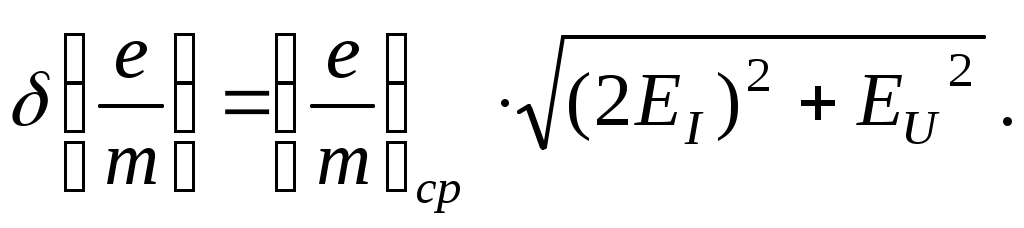
12*. Оцените полные абсолютную и относительную Е погрешности. Сделав необходимые округления, запишите окончательный результат измерений; сравните полученный доверительный интервал с табличными данными.
Контрольные вопросы
Методы определения удельного заряда элементарных частиц.
Движение заряженных частиц в электрическом поле. Ускоряющая разность потенциалов.
Сила Лоренца. Сила Ампера.
Движение заряженных частиц в магнитном поле. Траектории движения частиц в магнитном поле.
Виды и принцип действия ускорителей заряженных частиц.
Литература:
[4] - §43, 44, 72-76; [7] - §6.1-6.6; [12] - §111-116.
4. КОЛЕБАНИЯ И ВОЛНЫ
|
 Скачать 1.84 Mb.
Скачать 1.84 Mb.





