Методические указания к виртуальному лабораторному практикуму Вологда 2007

• Название: Методические указания к виртуальному лабораторному практикуму Вологда 2007
• Дата: 13.01.2022
• Размер: 1.84 Mb.
• Имя файла: virtlab (2).doc
• Тип: Методические указания; #330128
• страница: 11 из 24

Лабораторная работа № 4.1
ПРУЖИННЫЙ МАЯТНИК

Цель работы:   1) изучение свободных колебаний пружинного маятника;

2) экспериментальное определение коэффициента жесткости пружины и коэффициента сопротивления среды.
Схема экспериментальной установки



1 – пружина;
2 – груз;
3 – навески;
4 – съемный диск;
5 – линейка;
6 – секундомер


Рис. 1

Рис. 1.

Теория метода
Классический пружинный маятник (рис. 1) представляет собой подвешенный на пружине 1 жесткостью k груз 2 массой m. Из-за сравнительно малой силы сопротивления воздуха колебания такого маятника в течение длительного промежутка времени являются практически незатухающими. Их период определяется известной формулой

(1)

Зная массу груза m и период колебаний Т, из формулы (1) можно найти коэффициент жесткости пружины

(2)

Измерив секундомером 6 время нескольких (N) колебаний t, их период можно рассчитать как T = t/N. С учетом этого выражение (2) принимает вид

(3)

Для повышения точности результата измерений и оценки его случайной погрешности необходимо провести несколько опытов, изменяя с помощью навесок 3 массу груза m. Расчетную формулу (3) удобно представить в виде

, (4)

где

. (5)
Экспериментальная установка позволяет изучать и явно выраженные затухающие колебания. С этой целью к грузу 2 крепится съемный диск 4, наличие которого существенно увеличивает сопротивление воздуха.

Как известно, уравнение гармонических затухающих колебаний имеет вид

y(t) = A(t)cos(t + ₀), (6)

где y – координата (смещение от положения равновесия) груза; t – время; А – амплитуда колебаний;  – циклическая частота;  ₀ – начальная фаза. Для затухающих колебаний амплитуда и циклическая частота определяются выражениями:

A(t) = A₀exp(-t); (7)

(8)

где  A₀ – начальная амплитуда;  – коэффициент затухания, зависящий от коэффициента сопротивления среды b и массы колеблющегося груза:

; (9)

 ₀ – циклическая частота собственных (незатухающих) колебаний, связанная с их периодом известным соотношением  ₀ = 2/Т и, с учетом (1), равная

. (10)
Начальные амплитуда  A₀ и фаза  ₀ зависят от способа выведения маятника из положения равновесия (от начальных условий):

(11)

где y₀ – начальное смещение груза; v_y0 – проекция его скорости в начальный момент времени t = 0. Если v_y0 = 0 (пружина просто сжата (y₀ > 0) или растянута (y₀ < 0), а затем отпущена), то выражения (11) с учетом (8) примут вид

(12)

Часто на практике (в том числе и в данной лабораторной работе) коэффициент затухания мал по сравнению с собственной частотой колебаний: << ₀ . Анализ выражений (8) и (12) показывает, что в этом случае циклическая частота затухающих колебаний ₀ ; начальная фаза ₀  0; начальная амплитуда А₀  y₀ . Уравнение колебаний (6) с учетом зависимости амплитуды от времени (7) приближенно можно записать в виде

y(t)  y₀exp(-t)cos( ₀ t) . (13)

Для расчетов по этому уравнению необходимо знать величины y₀ ,  ₀ и  . Начальное смещение от положения равновесия y₀  может быть установлено и измерено с помощью линейки 5. Циклическая частота  ₀ определяется по формуле (10); масса груза m является заданной величиной; методика определения коэффициента жесткости пружины k описана выше. Для вычисления коэффициента затухания  по формуле (9) нужно знать коэффициент сопротивления среды b. Остановимся на методике определения этой величины.

Логарифмирование зависимости (7) дает



откуда



Выражая из формулы (9) коэффициент сопротивления b =2m, получим

. (14)
Вместо того, чтобы засекать момент времени t, в который измеряется амплитуда А, удобнее проводить измерения через определенное число колебаний маятника N и зафиксировать лишь время окончания измерений t_к . Если за промежуток времени t_к  произошло N_к полных колебаний, то их период Т = t_к / N_к , а время произвольного числа N колебаний определится как t = TN или

. (15)

Порядок измерений и обработки результатов

Упражнение 1. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ЖЕСТКОСТИ ПРУЖИНЫ
1. Выяснив рекомендуемое значение числа колебаний Nу преподавателя, время которых вы будете измерять (обычно N = 30), рассчитайте по формуле (5) константу С и запишите ее значение в тетрадь.

2. Освободите груз 2 от навесок 3 и диска 4.

3. Занесите значение массы груза m, выраженное в кг, во второй столбец табл. 1.

Таблица 1

Номер опыта	m, кг	t, c	k, Н/м	k, Н/м	(k)2, (Н/м)2
1
2
…	…	…	…	…	…
5
		=		=

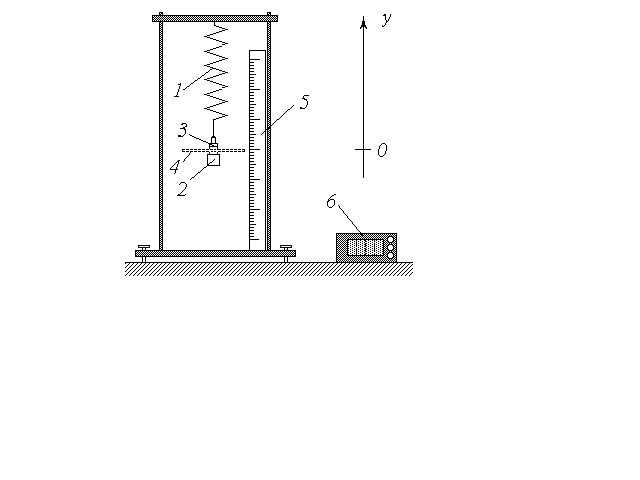
4. Выведите маятник из положения равновесия и отпустите. С помощью секундомера 6 измерьте время N полных колебаний и занесите результат в третий столбец таблицы.

5. Изменяя массу груза с помощью навесок 3, выполните пп. 3 и 4 еще четыре раза.

6. Для каждого из пяти проведенных опытов вычислите по формуле (4) коэффициент жесткости пружины; результаты занесите в четвертый столбец таблицы.

7. Найдите среднее значение коэффициента жесткости . Выполните все расчеты, необходимые для оценки случайной погрешности определения величины k. Задаваясь доверительной вероятностью  = 0,95; рассчитайте погрешность _sk.

8*. Определите абсолютные приборные ошибки прямых измерений массы m и времени t , а также относительные ошибки E_m и E_t .

9*. Найдите абсолютную приборную погрешность косвенного измерения коэффициента жесткости k. Для этого, если потребуется, используйте формулу



10*. Оцените полную абсолютную  и относительную Е погрешности. Сделав необходимые округления, запишите окончательный результат измерения коэффициента жесткости.

Упражнение 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА СОПРОТИВЛЕНИЯ СРЕДЫ

1. Прикрепите к грузу 2 съемный диск 4. С помощью навесок 3 установите рекомендуемое значение общей массы колеблющегося груза m и занесите его (в кг) в верхнюю строку табл. 2.

Таблица 2

m =кг				m =кг				m =кг
N	t, c	A, мм	b, кг/с	N	t, c	A, мм	b, кг/с	N	t, c	A, мм	b, кг/с
0	0		-	0	0		-	0	0		-
10				10				10
20				20				20
30				30				30
40				40				40

2. Приложив к измерительной линейке 5 полоску бумаги, отметьте на ней положение равновесия (для этого проведите горизонтальную черту против диска 4).

3. Запишите в табл. 2 в строку, соответствующую начальному моменту времени (N = 0; t = 0), рекомендуемое значение начального смещения груза y₀ = A₀ (в мм).

4. Сместите груз по вертикали на заданное расстояние y₀ ; отметьте положение диска чертой на полоске бумаги. Отпустите груз, одновременно включив секундомер.

5. Отсчитав N = 10 полных колебаний маятника, отметьте чертой крайнее положение диска; повторите то же для N = 20, 30 и 40 колебаний (маятник не останавливать). При достижении 40 колебаний выключите секундомер. Запишите значение времени 40 колебаний t_к в таблицу против N = N_к = 40.

6. По формуле (15) рассчитайте время t для N = 10, 20 и 30 колебаний; результаты занесите во второй столбец таблицы.

7. Измеряя с помощью линейки расстояние от положения равновесия до соответствующих отметок на бумажной полоске, определите и занесите в таблицу значения амплитуды А для N = 10, 20, 30 и 40.

8. Используя формулу (14), вычислите и занесите в таблицу значения коэффициента сопротивления воздуха b.

9. Повторите вышеописанные измерения и расчеты еще дважды. При этом, по рекомендации преподавателя, можете изменять массу m и начальное смещение y₀  (А₀ ).

10. Рассчитайте среднее из 12 полученных значений коэффициента b. 11. Задаваясь указанным преподавателем значением массы колеблющегося груза m, вычислите по формулам (10) и (9) собственную частоту колебаний ₀  и коэффициент затухания . При подстановке в формулы используйте средние значения коэффициентов жесткости пружины k и сопротивления воздуха b. Убедитесь в справедливости сделанного ранее допущения << ₀ .

12. Для заданного преподавателем начального смещения y₀  по уравнению (13) рассчитайте и постройте график зависимости y(t) в течение первых пяти полных колебаний (при расчетах помните, что фаза колебаний ( ₀t) имеет размерность радиан).
Контрольные вопросы

1. 
   Составьте дифференциальное уравнение гармонических колебаний для пружинного маятника, физического маятника.
   
2. 
   Гармонические колебания и их характеристики.
   
3. 
   Способы выведения колебательной системы из положения равновесия. Зависимость характеристик гармонических колебаний от начальных условий.
   
4. 
   Превращение энергии при гармонических колебаниях.
   
5. 
   Влияние сил сопротивления среды на процесс колебаний. Дифференциальное уравнение затухающих колебаний.
   
6. 
   Уравнение свободных затухающих колебаний. Зависимость амплитуды от времени. Коэффициент затухания. Логарифмический декремент затухания.
   
7. 
   Добротность колебательной системы.
   
8. 
   Вынужденные колебания. Уравнение вынужденных колебаний под действием гармонически изменяющейся силы.
   
9. 
   Автоколебания. Примеры автоколебательных систем.
   

Литература:
[3]- Гл. IX; [13]-Гл. 3.1-3.4.