Цель работы: 1) изучение характеристик затухающих электромагнитных колебаний;
2) экспериментальное определение параметров колебательного контура.
Схема экспериментальной установки
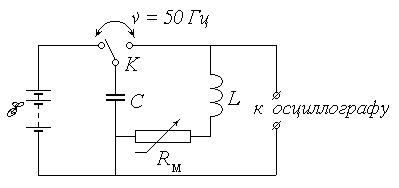
E – аккумуляторная батарея;
К – переключатель;
С – батарея конденсаторов;
L – катушка индуктивности;
R
Рис. 1
– магазин сопротивлений
Описание установки
Исследуемый в работе колебательный контур (рис. 1) состоит из батареи конденсаторов общей емкостью С (в дальнейшем для краткости будем называть ее конденсатором) и катушки, обладающей индуктивностью L и активным сопротивлением RL . Кроме того, в контур включен последовательно с катушкой магазин сопротивлений Rм , позволяющий изменять общее сопротивление контура R. Пренебрегая сопротивлением соединительных проводов, можно положить:
R = Rм + RL . (1)
Если установить переключатель К в левое положение, то конденсатор С будет заряжаться от батареи аккумуляторов с постоянной ЭДС E . Перевод переключателя в правое положение отключает конденсатор от источника и заставляет его разряжаться на цепь, состоящую из катушки и магазина сопротивлений; при этом, как известно, в контуре возникают электромагнитные колебания. Из-за наличия активного сопротивления R часть первоначального запаса энергии заряженного конденсатора затрачивается на выделение джоулева тепла, и колебания постепенно затухают.
Для наблюдения колебательного процесса служит осциллограф, основным элементом которого является электронно-лучевая трубка (ЭЛТ). Схема и принцип действия ЭЛТ описаны в указаниях к лабораторной работе 3.5.
Теория метода
Исследуемое напряжение (разность потенциалов на обкладках конденсатора) Uyподается на горизонтальные отклоняющие пластины, благодаря чему след электронного пучка на экране перемещается в вертикальном направлении Oy по закону, практически повторяющему закон изменения величины Uy : y(t) Uy (t). На вертикальные отклоняющие пластины подается так называемое напряжение развертки Ux , представляющее собой периодическое чередование пилообразных импульсов (рис. 2).
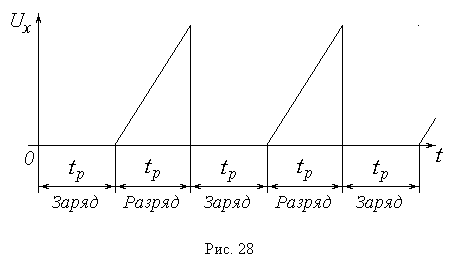
Рис. 2
След электронного пучка в пределах одного импульса развертки движется в горизонтальном направлении Ох всегда в одну и ту же сторону (для наблюдателя – слева направо) с постоянной скоростью, т.е. x(t)
t. В результате траектория светящейся точки на экране y(x) имеет вид графика зависимости напряжения Uy от времени t. Если подачу напряжения Uy, изменяющегося во времени по одному и тому же закону, повторять периодически с достаточно высокой частотой, согласованной с частотой развертки, то траектория y(x) не исчезнет с экрана, и осциллограмма будет представлять собой устойчивую картину графика функции Uy(t).
Периодическое чередование заряда и разряда конденсатора С осуществляется с помощью специального устройства – поляризованного электромагнитного реле. Реле заставляет переключатель К совершать колебания с частотой 50 Гц, т.е. с периодом Тп = 0,02 с. Первую половину периода переключатель замкнут в левом положении; при этом происходит заряд конденсатора от источника E . Вследствие синхронизации частоты и фазы развертки с частотой и фазой переключения реле в этот промежуток времени на вертикальные отклоняющие пластины ЭЛТ напряжение не подается, и след пучка на экране не перемещается по горизонтали; поэтому процесс зарядки конденсатора не «разворачивается» во времени.
Во второй половине периода длительностью tp= Tn /2 = 0,01 с переключатель замкнут в правом положении – происходит разряд конденсатора, сопровождаемый колебаниями; на вертикальные пластины подается линейно возрастающее напряжение, и на экране возникает картина колебаний. Благодаря высокой частоте переключений человеческий глаз воспринимает эту картину как неизменную во времени. Примерный вид осциллограммы затухающих колебаний показан на рис. 3.
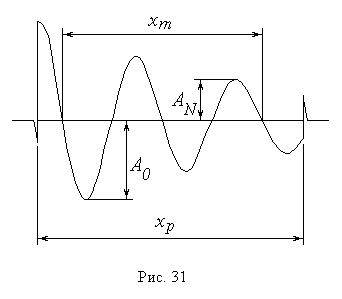 Переходные процессы, происходящие при переключе-ниях реле, обуславливают нали-чие характерных «всплесков» на осциллограмме, благодаря которым можно довольно точно определить расстояние хр , соответствующее длительности процесса разряда конденсатора tp . Это позволяет найти масштабный коэффициент Переходные процессы, происходящие при переключе-ниях реле, обуславливают нали-чие характерных «всплесков» на осциллограмме, благодаря которым можно довольно точно определить расстояние хр , соответствующее длительности процесса разряда конденсатора tp . Это позволяет найти масштабный коэффициент
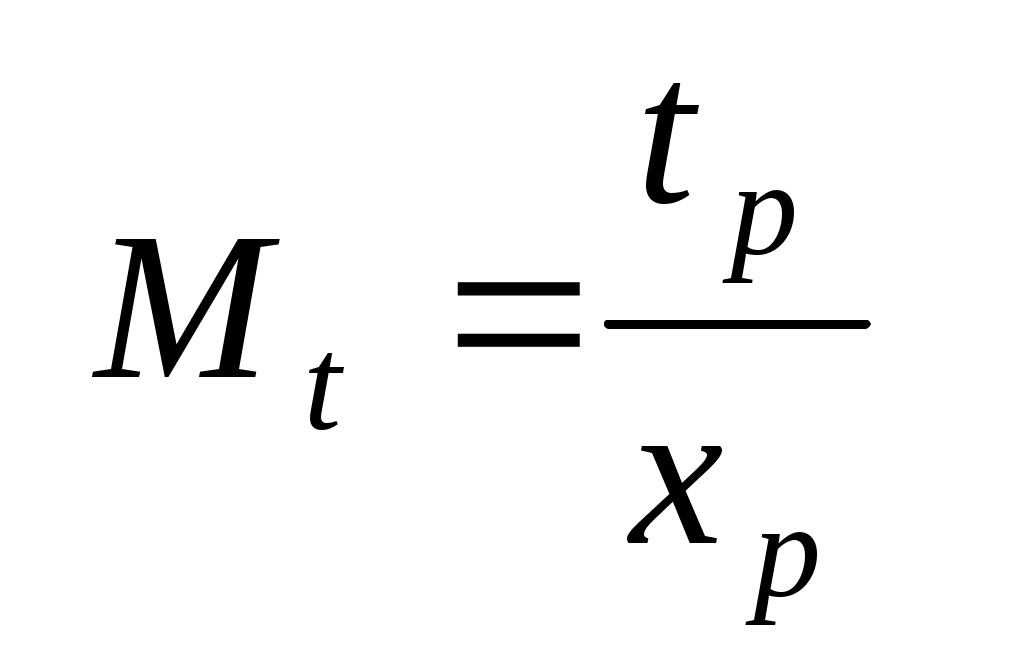
Рис. 3
, (2)
связывающий реальное время t с горизонтальной координатой на осциллограмме х; из очевидной пропорции 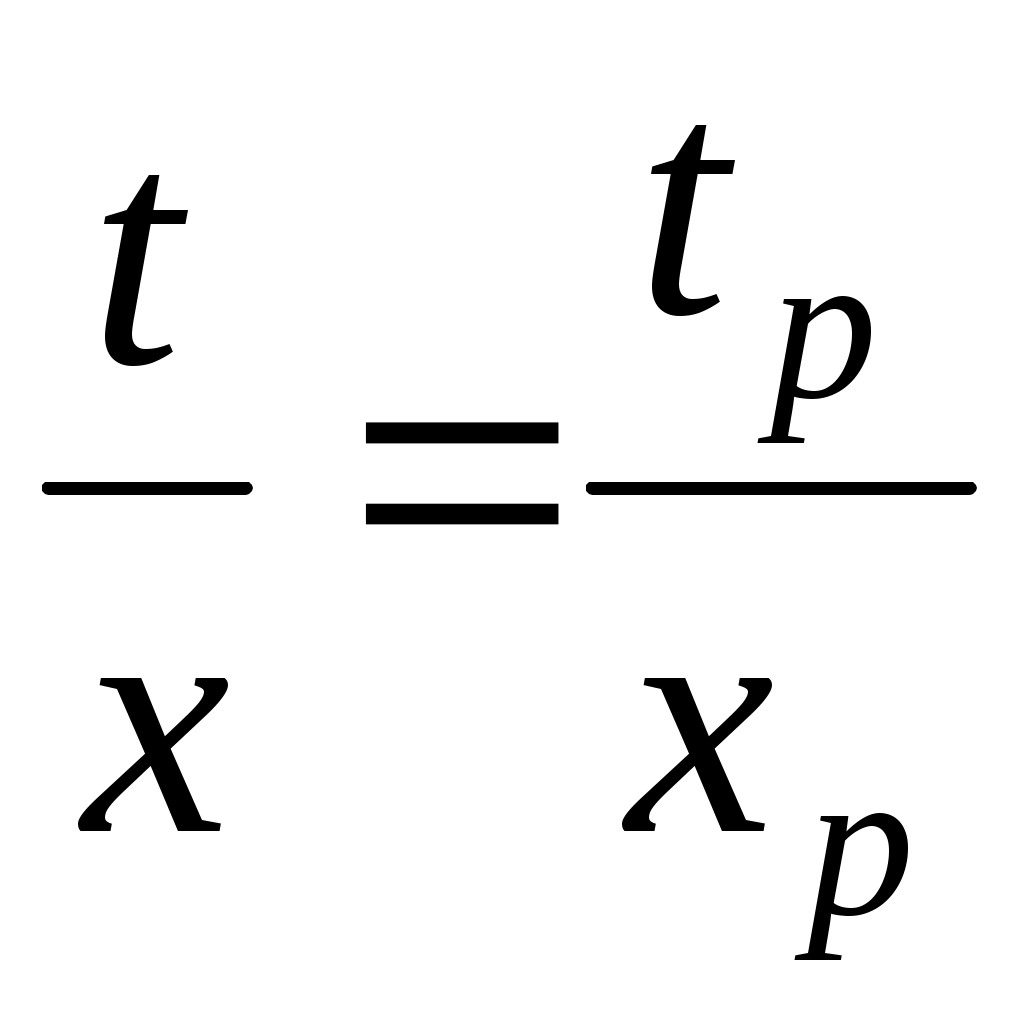 следует, что следует, что
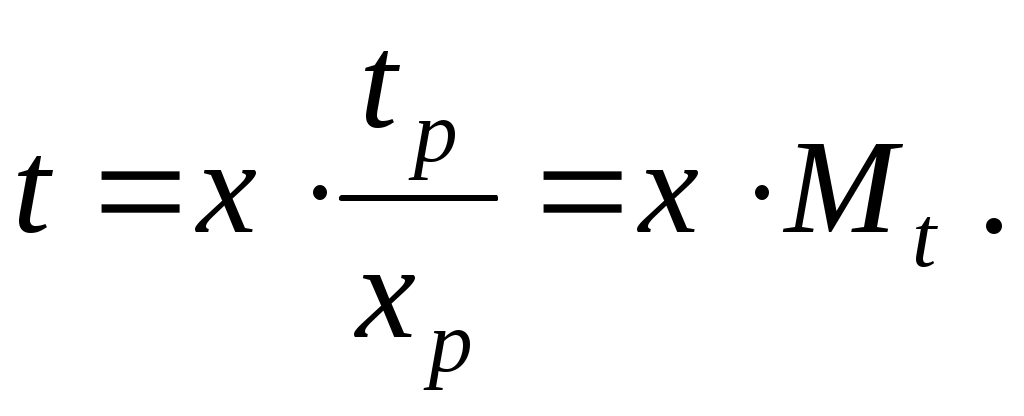 (3) (3)
Известно, что в реальном колебательном контуре при разряде конденсатора напряжение на его обкладках изменяется во времени согласно уравнению затухающих колебаний; аналогичный вид имеет и зависимость ординаты y на осциллограмме:
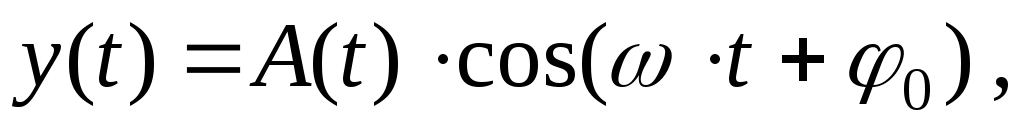
где A(t) – амплитуда; – циклическая частота; 0 – начальная фаза. Амплитуда изменяется во времени (затухает) по экспоненциальному закону
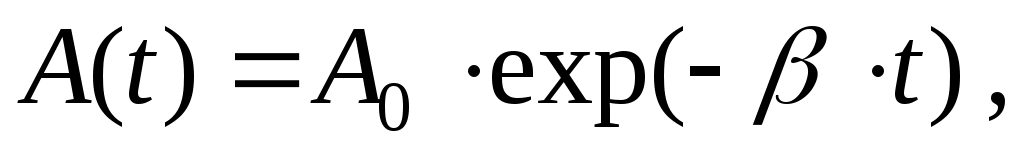 (4) (4)
где А0 – начальная амплитуда; – коэффициент затухания.
Величина связана с собственной частотой 0 колебаний идеального контура соотношением
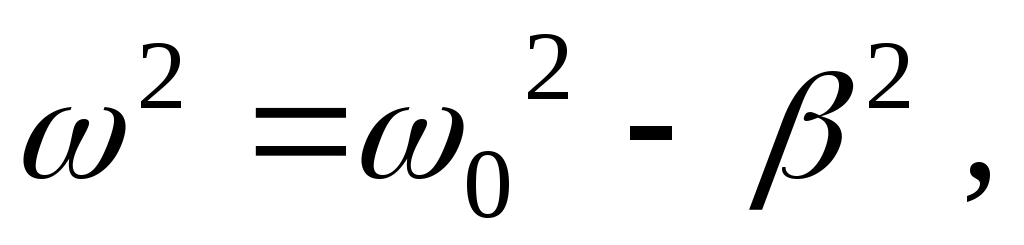 (5) (5)
а величины 0 и в свою очередь определяются значениями параметров контура L, C и R:
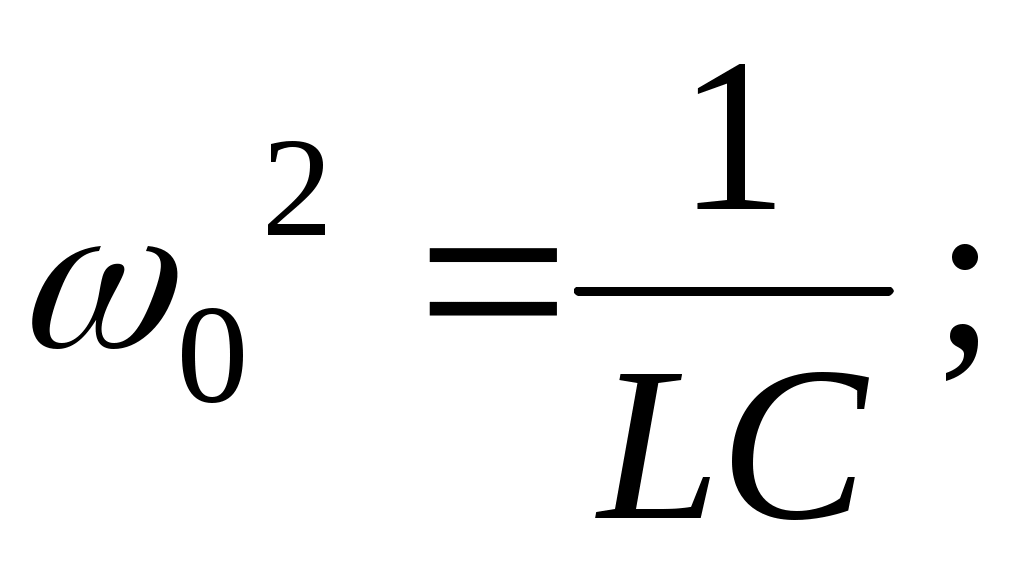 (6) (6)
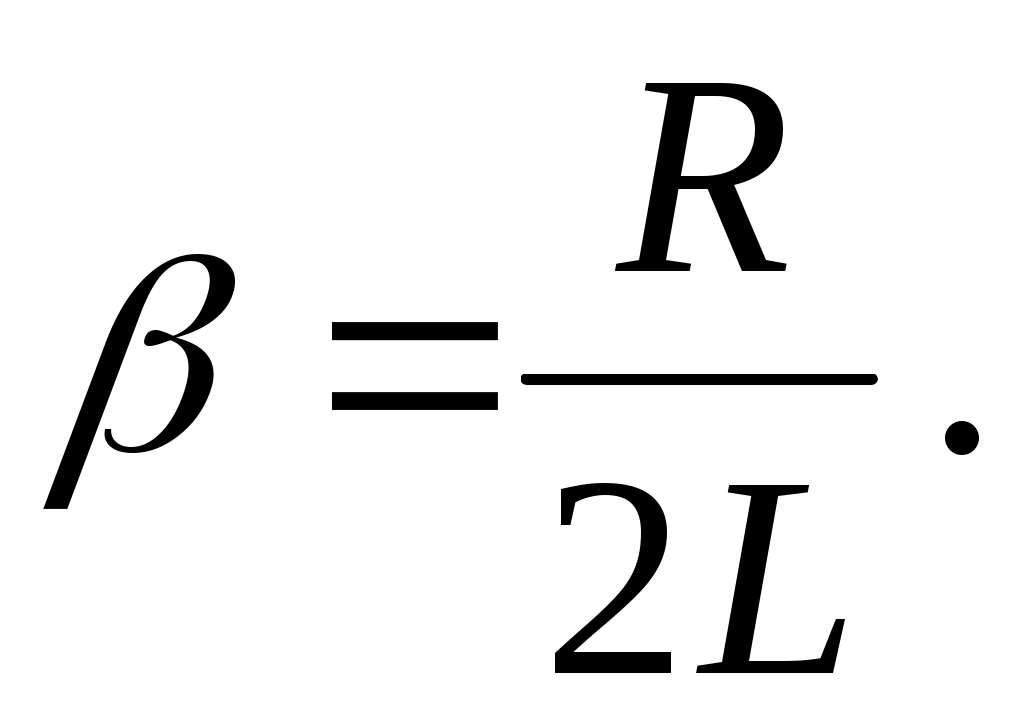 (7) (7)
Практическая цель данной работы заключается в определении неизвестных параметров контура по наблюдаемой на экране осциллографа картине затухающих колебаний. Соответствующая обработка осциллограммы позволяет найти важнейшие характеристики колебаний: период Т и коэффициент затухания .
Для определения периода необходимо измерить расстояние xm , соответствующее числу Nm колебаний. Это число может быть как целым, так и полуцелым, т.е. кратным ½ (в приведенном на рис. 3 примере Nm = 2). Следует отметить, что чем большее количество колебаний Nm будет «охвачено», тем точнее будет измерен их период. Соотношение (3) позволяет найти продолжительность Nm колебаний tm= xmMt и, следовательно, их период Т = tm /xm или
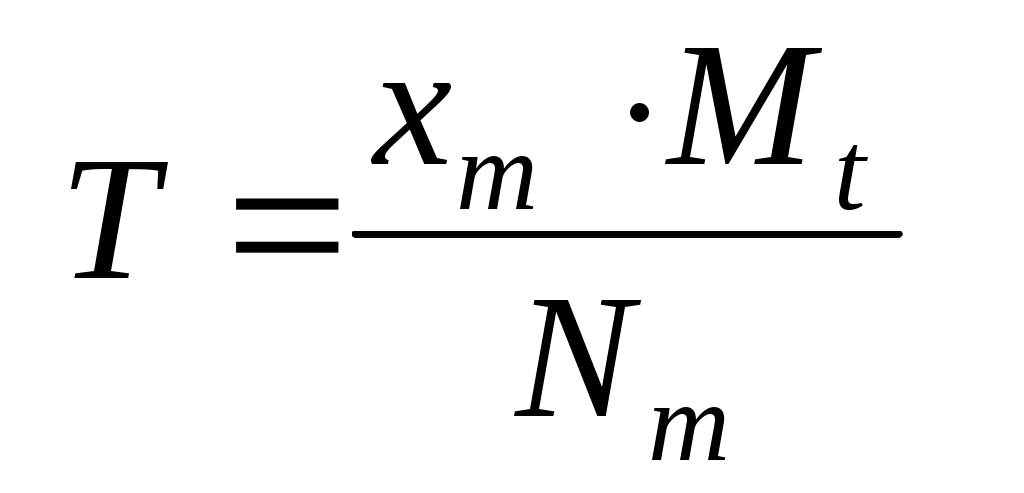 . (8) . (8)
Коэффициент затухания можно найти на основе зависимости (4):
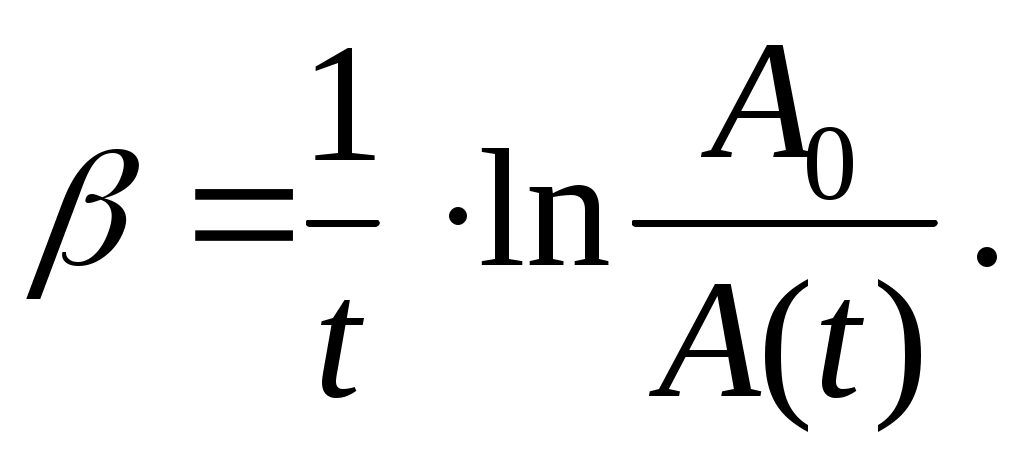 (9) (9)
Для практического определения величины необходимо измерить высоту А0 первого из явно наблюдаемых максимумов, а также высоту AN максимума, имеющего место спустя N колебаний после А0 . Число N также должно быть целым или полуцелым (в примере на рис. 3 N = 1,5). Промежуток времени t между выбранными таким образом максимумами можно представить как t = NT. В результате формула (9) примет вид
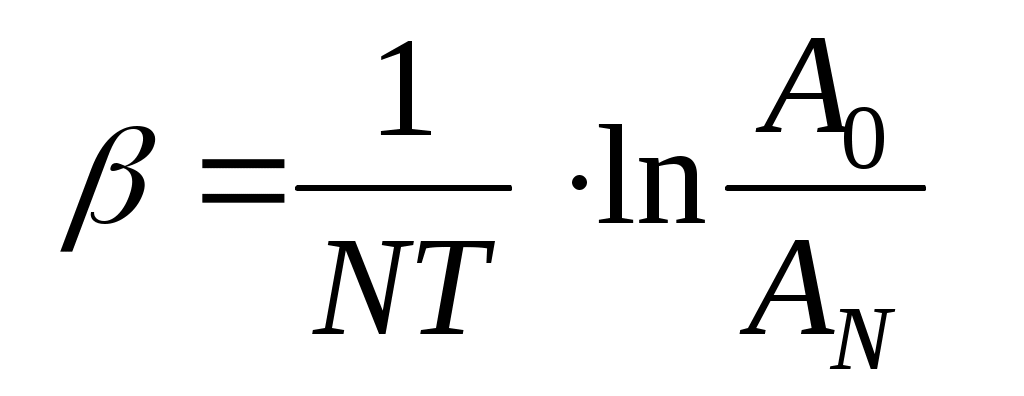 . (10) . (10)
Преобразуем выражение (7) с учетом (1):
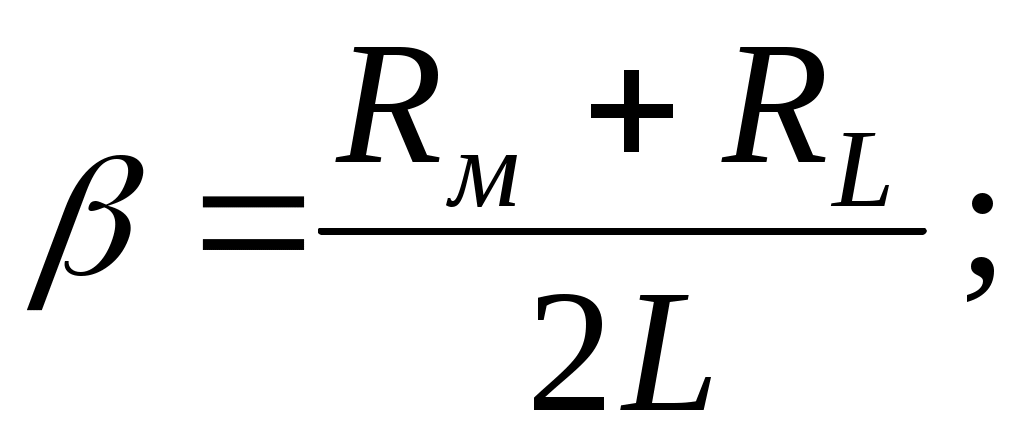
вводя обозначения:
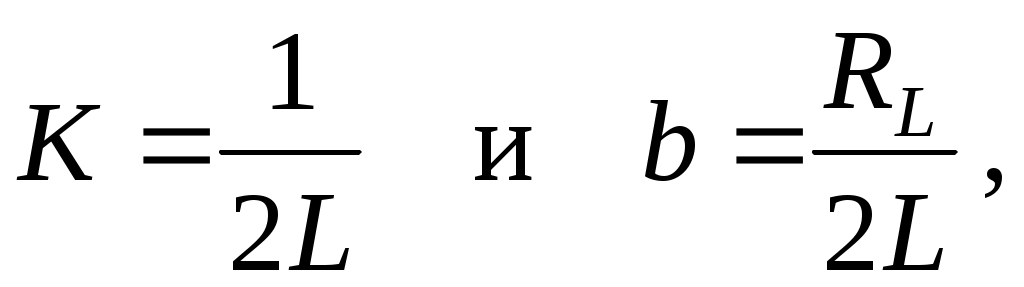
получим
= KRм + b, (11)
т.е. линейную зависимость коэффициента затухания от сопротивления магазина. Проведя несколько опытов по определению при различных значениях Rм , можно определить неизвестные коэффициенты K и b этой зависимости одним из применяемых для этого методов (графическим или методом наименьших квадратов). После этого легко рассчитать индуктивность L и сопротивление RL катушки как
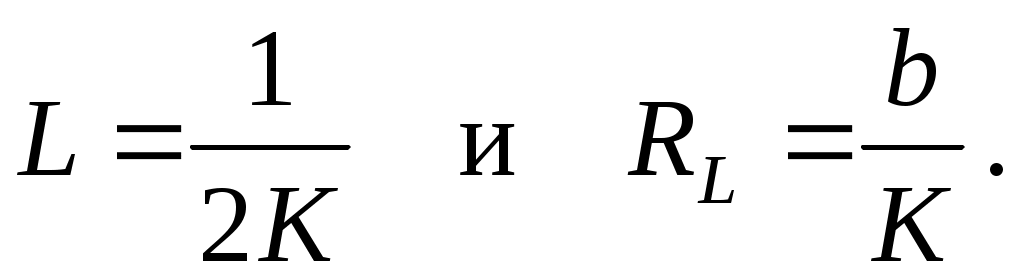 (12) (12)
После того, как найдены параметры катушки, емкость конденсатора С можно найти из выражения (6):
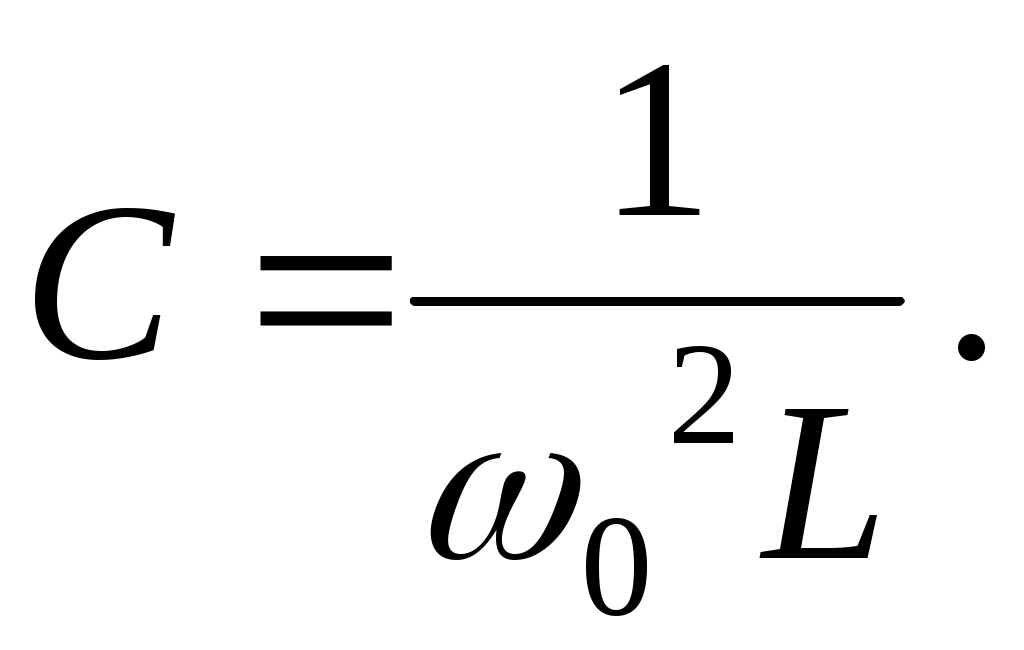
Из (5) следует, что 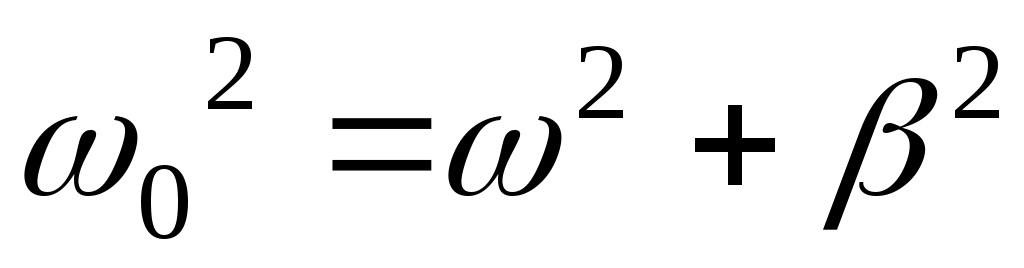 . Циклическая частота связана с периодом колебаний Т известным соотношением . Циклическая частота связана с периодом колебаний Т известным соотношением 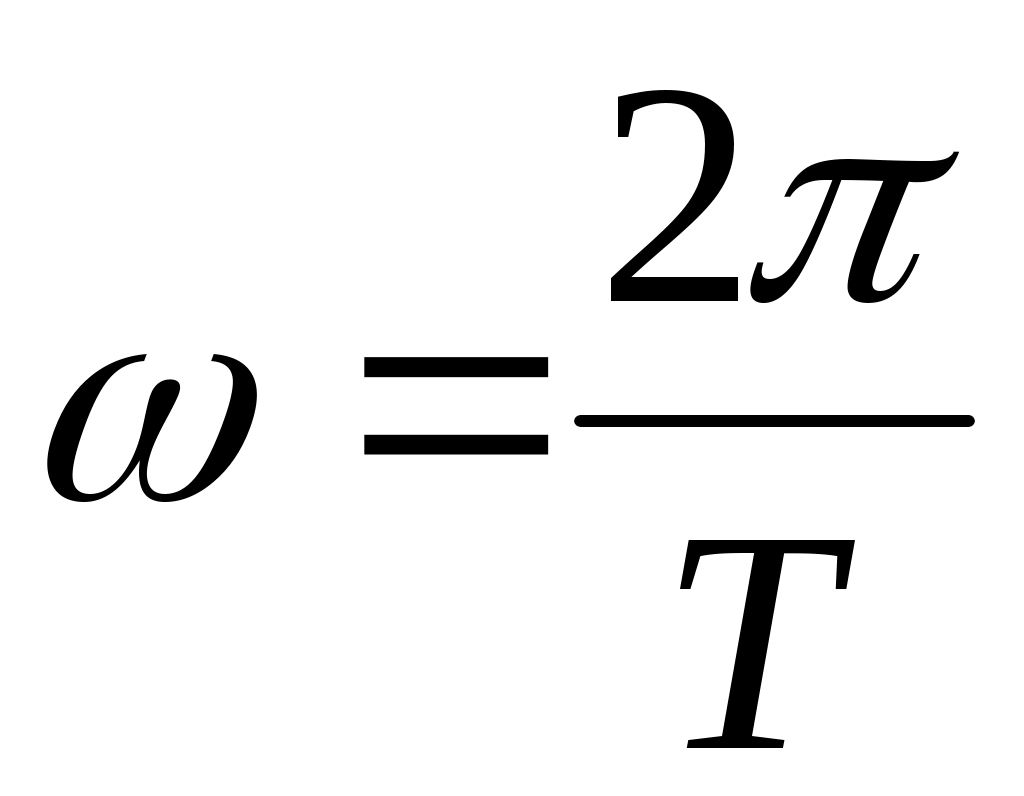 . С учетом этого получим: . С учетом этого получим:
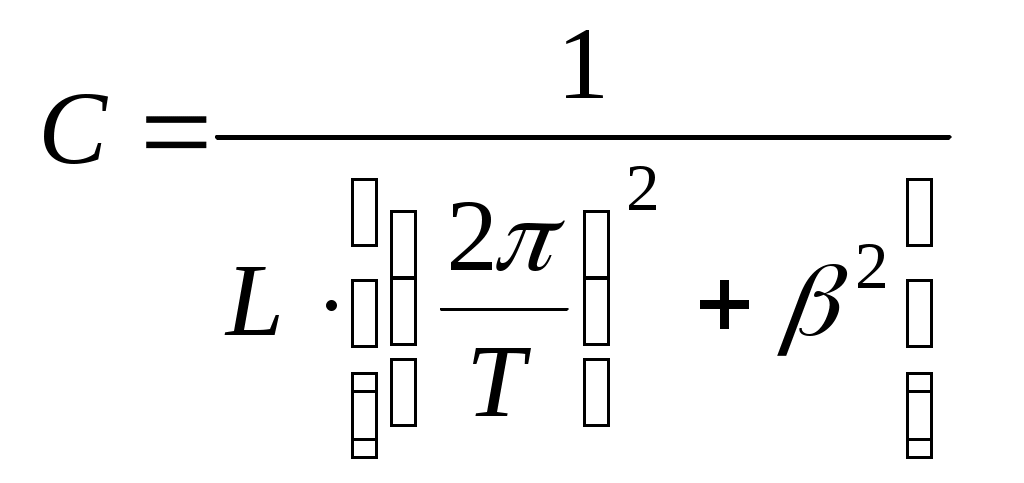 . (13) . (13)
Порядок измерений и обработки результатов
1. Ознакомьтесь с лабораторной установкой.
2. Установите с помощью магазина рекомендуемое значение сопротивления Rм .
3. Зарисуйте на клетчатой или миллиметровой бумаге наблюдаемую осциллограмму.
4. Изменяя величину Rм в соответствии с рекомендациями, повторите пп. 2, 3 еще не менее четырех раз.
5. Измерив расстояние хр (см. рис. 3) в миллиметрах, рассчитайте по формуле (2) и запишите в тетрадь масштабный коэффициент Mt в с/мм. Этот пункт выполняется один раз для одной из полученных осциллограмм.
6. Для каждого из проделанных опытов проведите обработку осциллограммы в следующем порядке.
6.1. Определите максимально возможное число наблюдаемых колебаний Nm и измерьте соответствующее расстояние xm . По формуле (8) вычислите период колебаний Т. Занесите результаты измерений и вычислений в таблицу.
6.2. Измерьте высоту А0 первого из четко наблюдаемых максимумов, а также высоту AN максимума, следующего через N колебаний после него. Рассчитайте коэффициент затухания по формуле (10). Результаты занесите в таблицу.
Номер опыта
|
Rм ,
Ом
|
Nm
|
хm ,
мм
|
Т,
с
|
А0 ,
мм
|
N
|
AN ,
мм
|
,
с -1
|
С,
мкФ
|
1
|
|
|
|
|
|
|
|
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
5
|
|
|
|
|
|
|
|
|
|
7. Нанесите экспериментальные точки на график зависимости (Rм). Убедившись в линейном характере этой зависимости, одним из известных вам способов определите коэффициенты K и b функции (11), а затем найдите значения индуктивности L и сопротивления RL катушки по формулам (12).
8. Для каждого из опытов рассчитайте по формуле (13) емкость конденсатора С; вычислите среднее значение этой величины.
Контрольные вопросы
Электромагнитные колебания. Идеальный колебательный контур. Амплитуда и частота собственных колебаний. Формула Томсона.
Реальный колебательный контур. Затухающие колебания. Коэффициент затухания; логарифмический декремент затухания.
Энергия электрического поля конденсатора и магнитного поля катушки. Превращения энергии при затухающих электромагнитных колебаниях.
Вынужденные колебания в последовательной RLC – цепи. Резонанс напряжений. Добротность колебательного контура.
Вынужденные колебания в параллельной RLC – цепи. Резонанс токов.
Применение метода векторных диаграмм для расчета цепей переменного тока.
Работа и мощность переменного тока, действующее (эффективное) значение напряжения переменного тока.
Принцип получения переменного тока.
Литература:
[4]- §99-102; [7]-§11.1-11.4.
|
 Скачать 1.84 Mb.
Скачать 1.84 Mb.


 Переходные процессы, происходящие при переключе-ниях реле, обуславливают нали-чие характерных «всплесков» на осциллограмме, благодаря которым можно довольно точно определить расстояние хр , соответствующее длительности процесса разряда конденсатора tp . Это позволяет найти масштабный коэффициент
Переходные процессы, происходящие при переключе-ниях реле, обуславливают нали-чие характерных «всплесков» на осциллограмме, благодаря которым можно довольно точно определить расстояние хр , соответствующее длительности процесса разряда конденсатора tp . Это позволяет найти масштабный коэффициент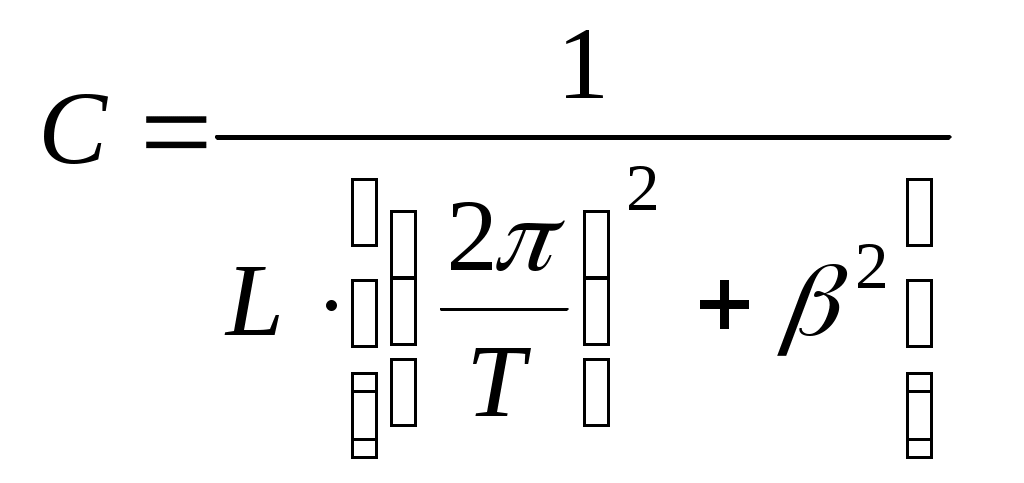 . (13)
. (13)