Цель работы: 1) наблюдение картины дифракции Фраунгофера от одиночной щели и дифракционной решетки в монохроматическом свете;
2) экспериментальное определение ширины щели и периода дифракционной решетки
Схема экспериментальной установки
1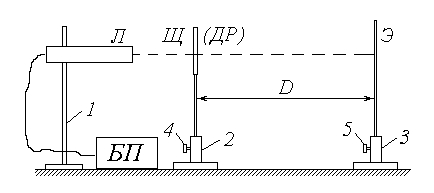 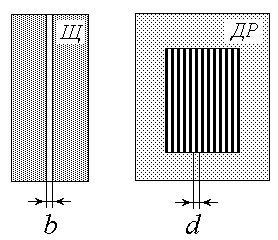
, 2, 3 – штативы; 4, 5 – регулировочные винты; Л – газовый лазер;
БП – блок питания лазера; Щ – пластинка со щелью;
ДР – дифракционная решетка; Э – экран
Теория метода
Установка для изучения дифракции света аналогична той, которая используется для наблюдения интерференционной картины в работе 5.1. Различие между ними заключается в том, что вместо пластинки П с горизонтальными щелями используется пластинка Щ с одной вертикальной щелью (упражнение 1) и дифракционная решетка ДР (упражнение 2). Их увеличенное схематическое изображение дано на схеме установки справа.
Рассмотрим прохождение через щель шириной b нормально падающей на нее плоской световой волны (на рис. 1 показан «вид сверху»). Согласно принципу Гюйгенса-Френеля каждая точка фронта волны (следовательно, каждая точка плоскости щели) является источником вторичных волн, распространяющихся во всех направлениях и заходящих в область геометрической тени. Так как эти вторичные волны когерентны, при наложении друг на друга они дают на экране Э картину интерференции. Сложность анализа этой картины заключается в необходимости учета бесконечного множества источников когерентных волн.
Р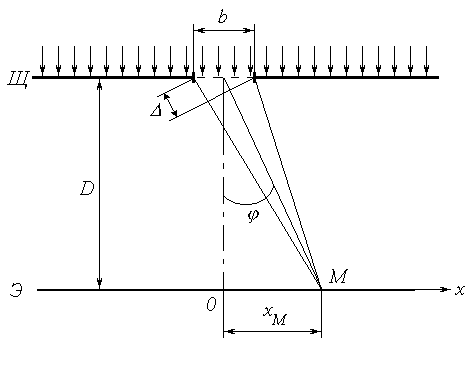
ис. 1
Выясним результат наложения лучей в произвольной точке экрана М, расположенной на расстоянии xM от центра картины (ось Ох направлена горизонтально в плоскости экрана). Если ширина щели b и расстояние xM малы по сравнению с расстоянием D от щели до экрана (b << DиxM<< D), то попадающие в точку М лучи практически параллельны друг другу и составляют с первоначальным направлением распространения некоторый малый угол . Результат интерференции вторичных волн зависит от величины этого угла, и интенсивность света в точке М определяется выражением
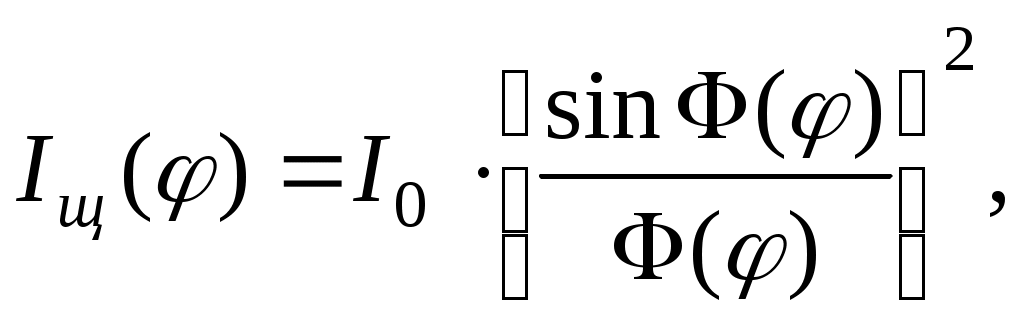 (1) (1)
где
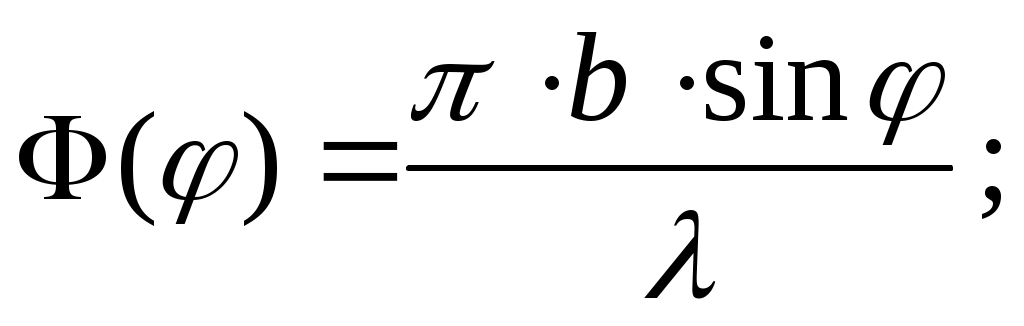 (2) (2)
I 0 – интенсивность света, идущего от всей щели в направлении первичного пучка; – длина волны света.
Из (2) следует, что (0) = 0; учитывая первый замечательный предел
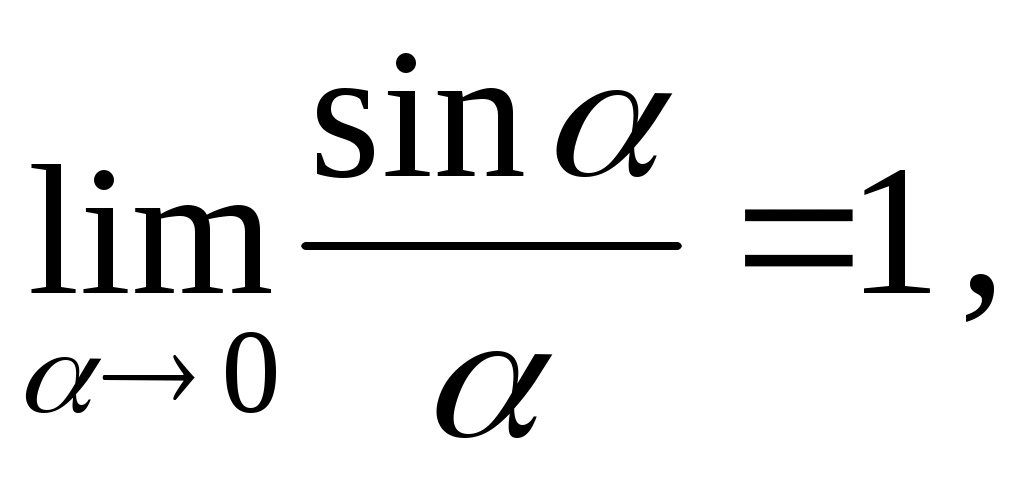
получим, что при = 0 (в центре картины) имеет место максимум освещенности: Iщ(0) = I 0 .
Функция (1) обращается в нуль при условии () = m, где m N. Подставляя в это условие выражение (2), получим уравнение, позволяющее определить углы, при которых наблюдаются минимумы освещенности (темные полосы):
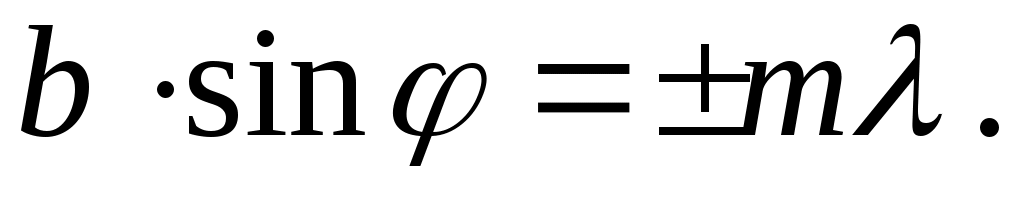 (3) (3)
Условие (3) можно также получить, воспользовавшись методом зон Френеля. Разобьем фронт волны (плоскость щели) на участки, разность хода от которых до точки М равна половине длины волны; так как соответствующая разность фаз равна , волны от двух таких соседних зон при наложении гасят друг друга. Таким образом, если для данной точки открыто четное число зон Френеля, то в ней наблюдается минимум интенсивности. Число зон можно найти, разделив разность хода крайних лучей (см. рис. 1) на половину длины волны. Учитывая, что 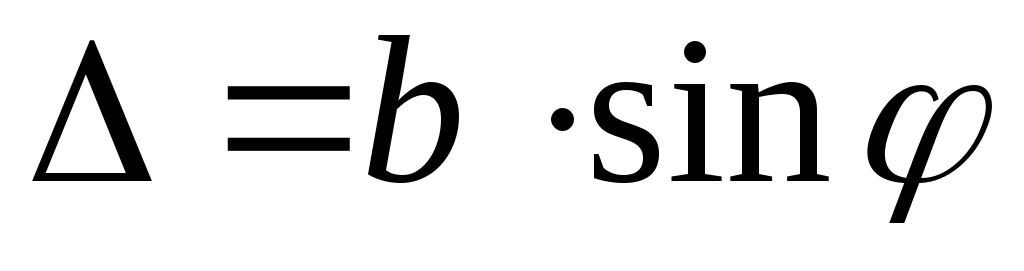 и положив количество зон равным четному числу 2m, придем к условию (3). и положив количество зон равным четному числу 2m, придем к условию (3).
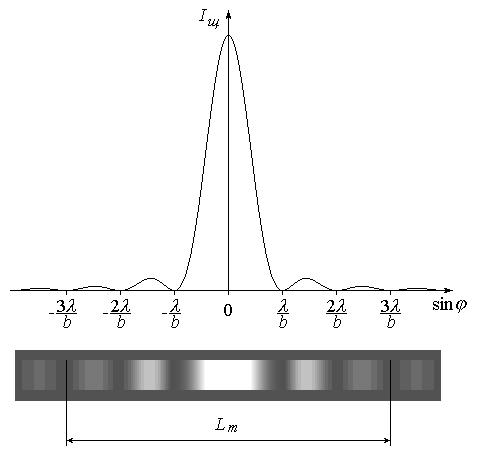
Между определяемыми этим условием минимумами наблюдаются слабо выраженные максимумы. На рис. 2 показан график зависимости интенсивности от синуса угла дифракции и соответствующая ему дифракционная картина на экране.
Рис. 2
Как видно из рис. 2, координата х точки М на экране (индекс «М» при х здесь и в дальнейшем опустим) связана с углом простым соотношением x = Dtg. Поскольку угол мал, имеем
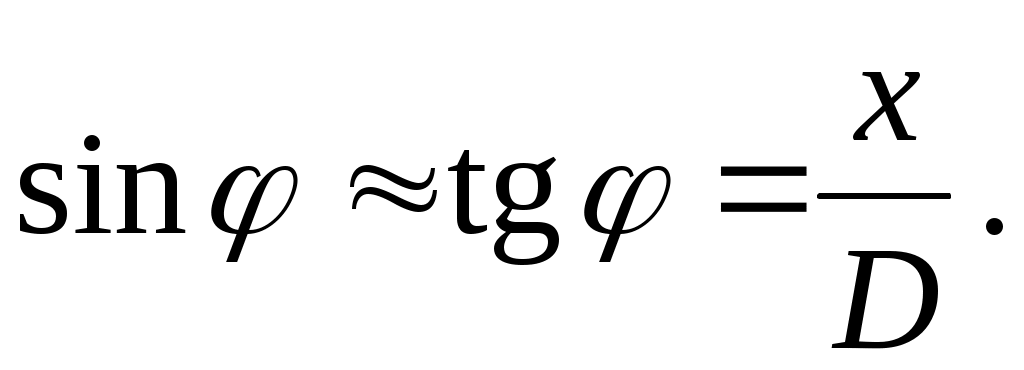 (4) (4)
Подставляя данное соотношение в условие (3), найдем координаты точек xm , в которых имеет место m-й по счету, начиная от центра, минимум освещенности. Ограничившись положительной полуосью (x >0), получим:
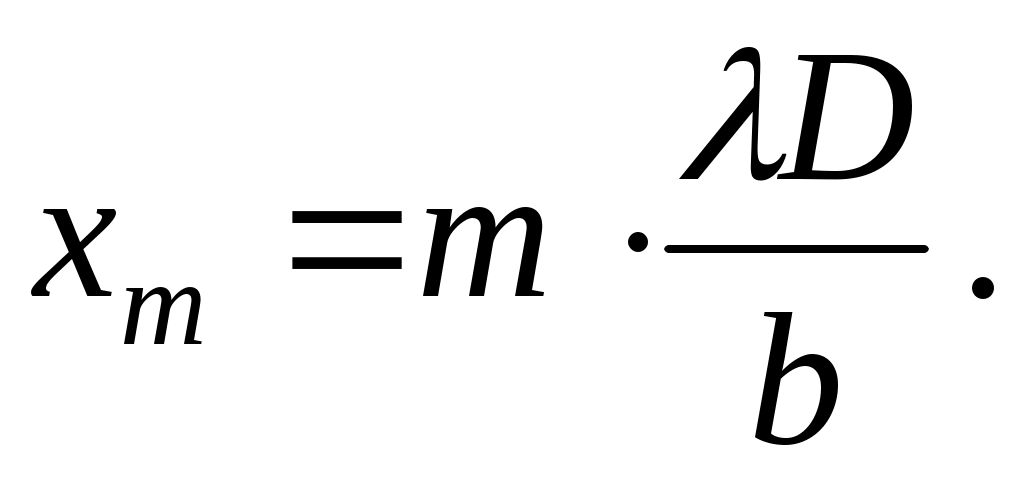 (5) (5)
Координату m-го минимума можно найти экспериментально путем обработки дифракционной картины (рис. 2). Для этого необходимо отметить по обе стороны от центрального максимума минимумы одного и того же порядка m (в примере на рисунке m = 3) и измерить расстояние между ними Lm ; расстояние от центра картины до m-го минимума находится из очевидного соотношения
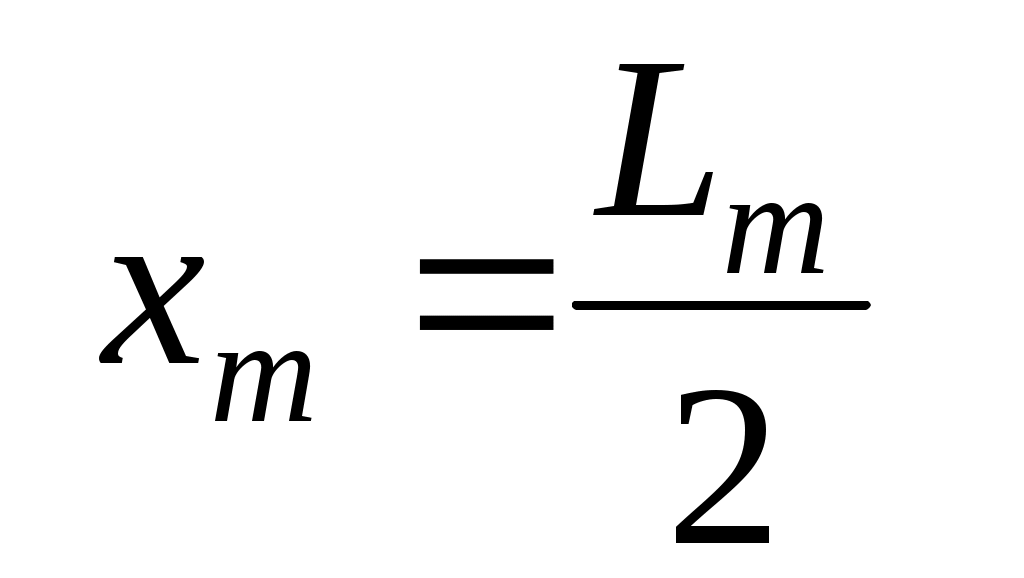 . (6) . (6)
Если известна длина волны лазерного излучения и расстояние от щели до экрана D, то с помощью выражения (5) можно определить ширину щели b:
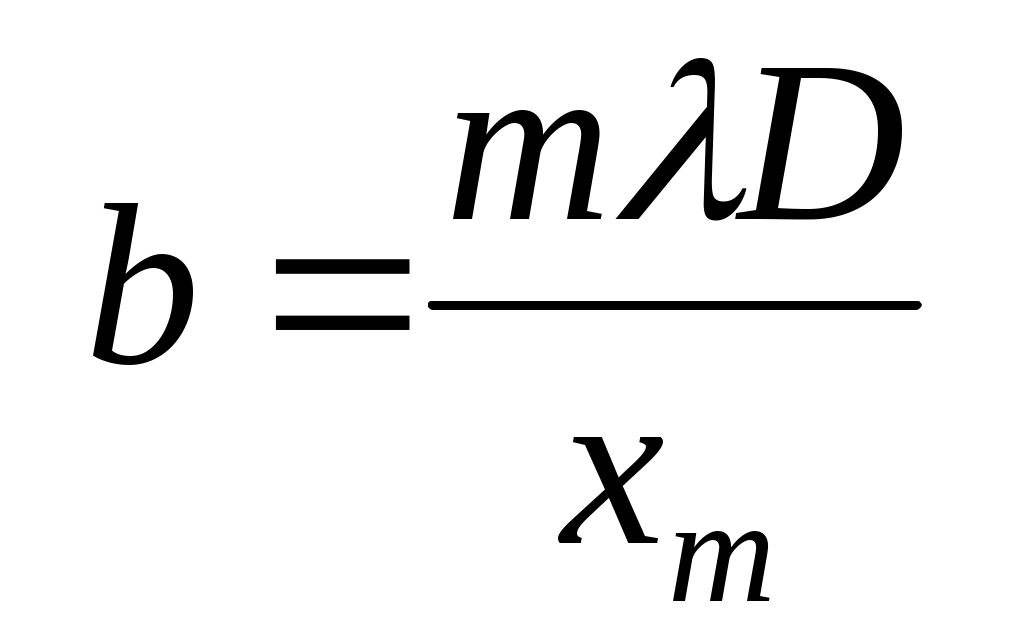 
. (7)
Рис. 3
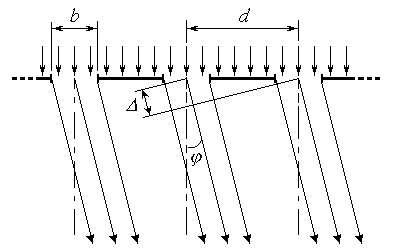
Дифракционная решетка (ДР) представляет собой пластинку с множеством параллельных узких щелей одинаковой ширины b, находящихся на расстоянии d друг от друга (рис. 3). Расстояние между центрами соседних щелей d называется постоянной (или периодом) дифракционной решетки.
При прохождении через решетку нормально падающей на нее плоской световой волны (см. рис. 3) происходят следующие явления: 1) интерференция вторичных волн, создаваемых точками в плоскости каждой из щелей (это явление подробно рассмотрено выше); 2) интерференция световых пучков от различных щелей. В результате наложения этих явлений на экране наблюдается дифракционная картина, имеющая довольно сложный характер. Так же, как и при дифракции от одиночной щели, интенсивность света в точке М экрана зависит от угла дифракции ; в случае решетки она определяется выражением
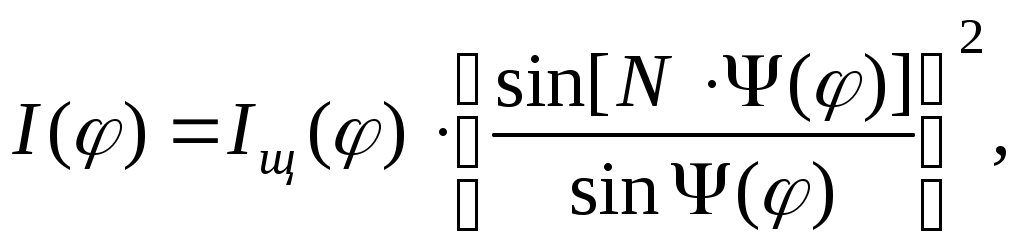 (8) (8)
где
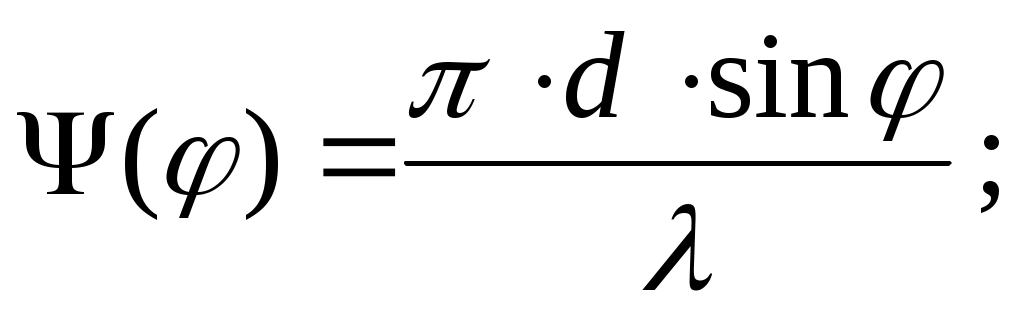 (9) (9)
N – общее число щелей (штрихов) решетки, накрываемых падающей световой волной; Iщ() – функция, определяемая выражениями (1)-(2).
Благодаря множителю Iщ() выражение (8) обращается в нуль при углах дифракции, определяемых условием (3); применительно к решетке оно является условием наблюдения главных минимумов.
Найдем значение I() при () = k, где k Z . Раскрыв неопределенность в фигурных скобках выражения (8), вычислим предел:
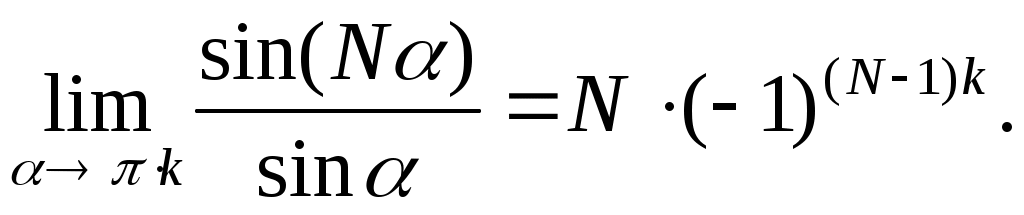
Интенсивность света при этом будет равна N 2Iщ . Условие () = k с учетом выражения (9) имеет вид
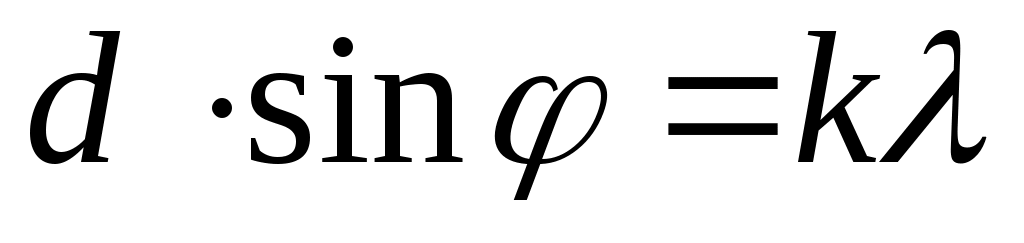 (10) (10)
и определяет углы, под которыми наблюдаются главные максимумы освещенности. Число k называется порядком главного максимума. В частности, при k = 0 и, следовательно, = 0 (в центре картины) имеет место наиболее яркий центральный максимум интенсивностью Imax= N 2I0 . Все остальные главные максимумы имеют меньшую интенсивность, зависящую от множителя Iщ().
Отметим, что условие главного максимума (10) можно получить на основе более простых соображений. Как было показано в описании к работе 5.1, пучки света от соседних щелей усиливают друг друга, если разность хода между ними кратна целому числу длин волн. Из рис. 3 видно, что в случае дифракционной решетки 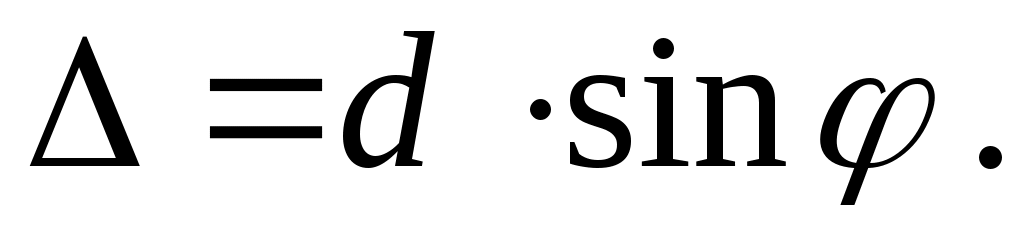 Подставляя это соотношение в вышеупомянутое условие, придем к (10). Подставляя это соотношение в вышеупомянутое условие, придем к (10).
Дробь в фигурных скобках выражения (8) обращается в нуль при 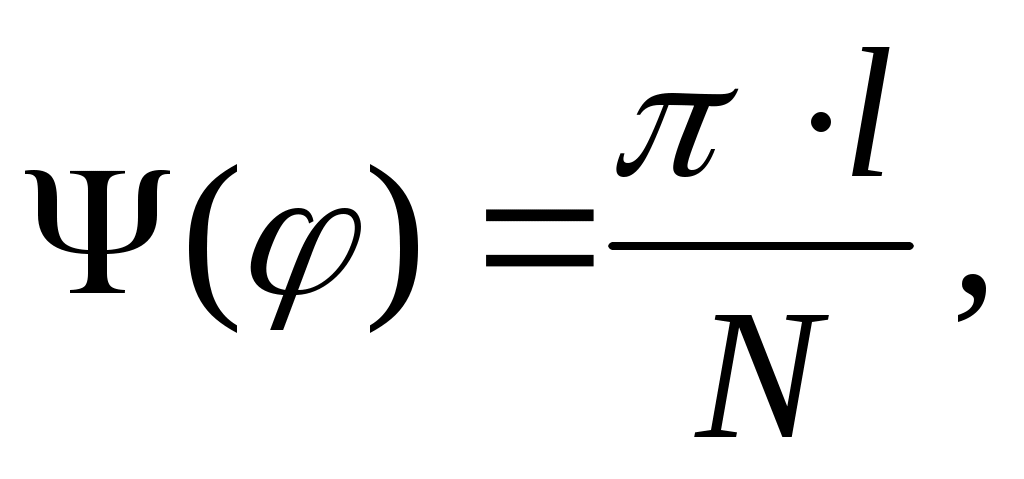 где l – целое число, не равное kN. Поэтому в промежутках между соседними главными максимумами наблюдается по (N –1) вторичных минимумов, чередующихся со слабо выраженными вторичными максимумами. При большом числе щелей N интенсивность самого яркого вторичного максимума составляет менее 5% интенсивности ближайшего главного максимума. В условиях данной лабораторной работы вторичные максимумы практически неразличимы и образуют бледную светлую полосу, на фоне которой в виде ярких пятен наблюдаются главные максимумы. где l – целое число, не равное kN. Поэтому в промежутках между соседними главными максимумами наблюдается по (N –1) вторичных минимумов, чередующихся со слабо выраженными вторичными максимумами. При большом числе щелей N интенсивность самого яркого вторичного максимума составляет менее 5% интенсивности ближайшего главного максимума. В условиях данной лабораторной работы вторичные максимумы практически неразличимы и образуют бледную светлую полосу, на фоне которой в виде ярких пятен наблюдаются главные максимумы.
На рис. 4 показан график зависимости интенсивности I от sin и соответствующая ему дифракционная картина на экране.
Р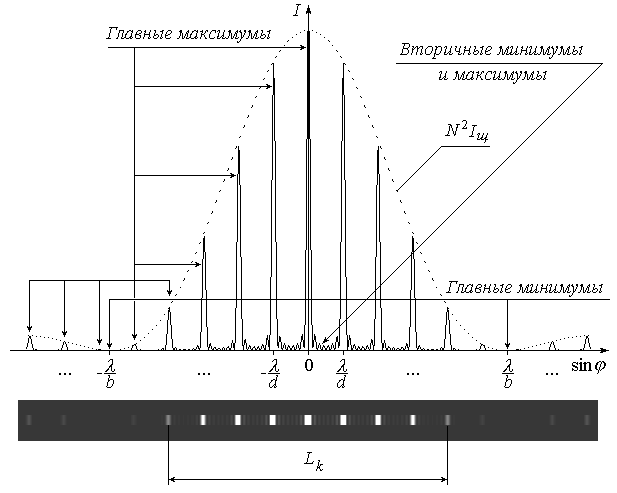
ис. 4
Так же, как и при дифракции на одиночной щели, в данном случае координата х на экране и угол дифракции связаны соотношением (4), с учетом которого условие (10) позволяет определить координату k-го главного максимума:
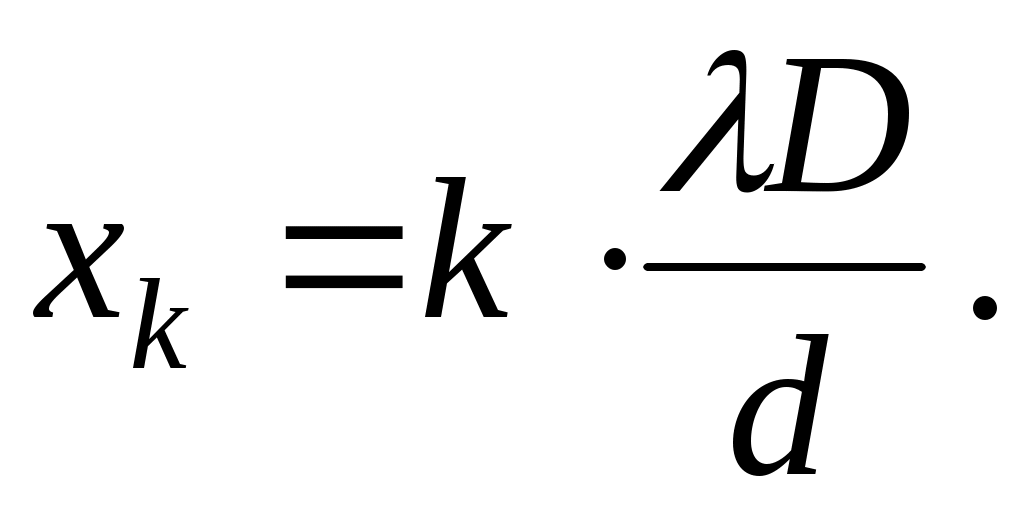 (11) (11)
Экспериментально значение хk можно найти путем обработки дифракционной картины. Для этого слева и справа от центрального максимума нужно отметить положения главных максимумов одного и того же k-го порядка (в примере на рис. 4 k = 4) и измерить расстояние между ними Lk , после чего определить координату xk как
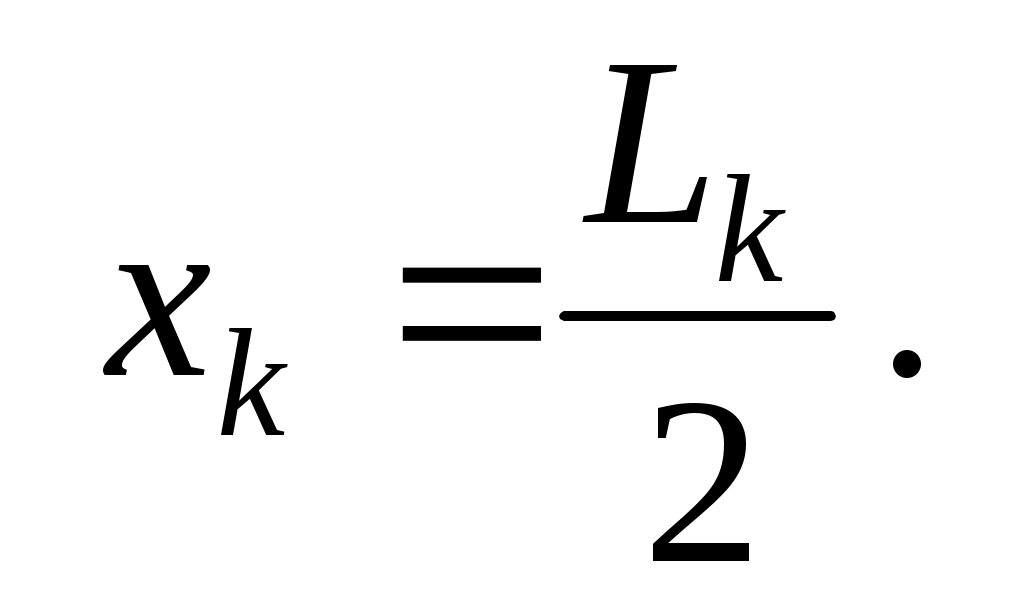 (12) (12)
Зная xk , а также расстояние от решетки до экрана D и длину волны света , из выражения (11) можно найти период дифракционной решетки:
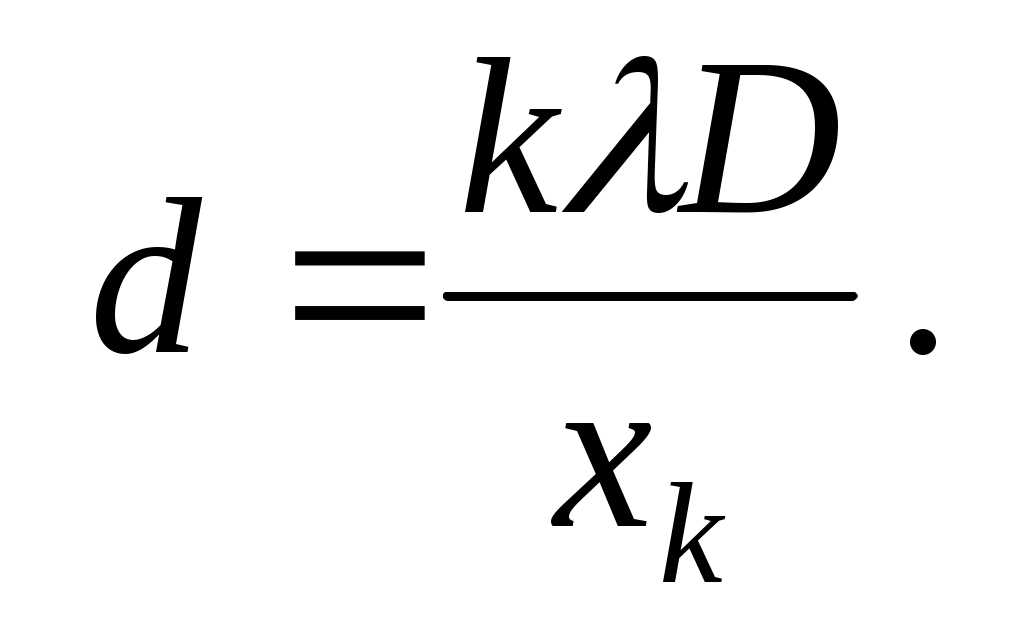 (13) (13)
Порядок измерений и обработки результатов
Упражнение 1. ОПРЕДЕЛЕНИЕ ШИРИНЫ ЩЕЛИ
1. Ознакомьтесь с приборами на рабочем столе; между лазером Л и экраном Э поместите пластинку Щ с вертикальной щелью.
2. Подключите к сети блок питания БП лазера. С помощью тумблера на панели БП включите лазер.
3. Запишите в тетрадь значение длины волны лазерного излучения = 0,633 мкм.
4. Установите экран Э так, чтобы на нем наблюдалась четкая дифракционная картина.
5. Запишите значение D в табл. 1, выразив его в миллиметрах.
Таблица 1
Номер опыта
|
D,
мм
|
m
|
Lm ,
мм
|
хm ,
мм
|
b,
мкм
|
b,
мкм
|
(b)2,
мкм2
|
1
|
|
|
|
|
|
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
n
|
|
|
|
|
|
|
|
|
|
|
|
=
|
|
=
|
|
6. Отсчитайте слева и справа от центра картины одинаковое число m минимумов; измерьте линейкой расстояние между ними Lm (см. рис. 2). Значения m и Lm (в мм) занесите в таблицу.
7. Изменяя расстояние D между щелью и экраном, повторите пп. 4-6 еще три-четыре раза (так, чтобы общее число опытов n было не менее четырех).
8. Для каждого опыта с помощью соотношения (6) найдите координату m-го минимума xm . По формуле (7) рассчитайте ширину щели b; последнюю выразите в мкм. Значения xm и b занесите в таблицу.
9. Вычислите сумму найденных значений ширины щели и определите ее среднее значение 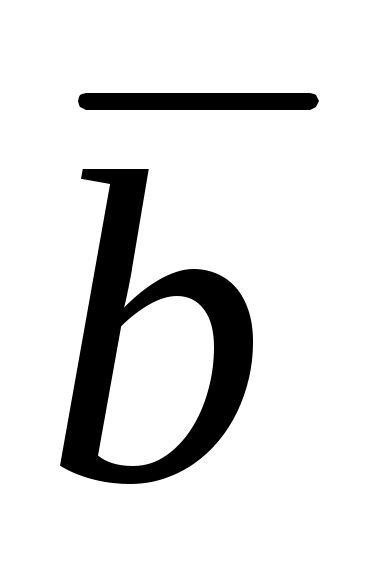 . .
10*. Выполните все расчеты, необходимые для оценки случайной погрешности измерения ширины щели s b. Найдите величину s b, задаваясь доверительной вероятностью = 0,95.
11*. Оцените абсолютные приборные ошибки прямых измерений D и Lm , а также относительные ошибки ED и EL . Найдите абсолютную приборную погрешность косвенного измерения b, при необходимости воспользовавшись формулой:
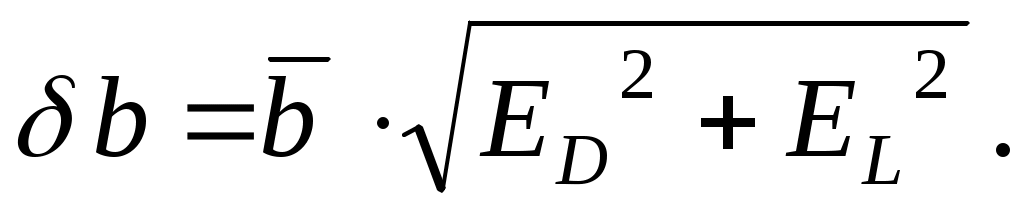
12*. Оцените полные абсолютную и относительную Е погрешности. Сделав необходимые округления, запишите окончательный результат измерения ширины щели.
Упражнение 2. ОПРЕДЕЛЕНИЕ ПЕРИОДА ДИФРАКЦИОННОЙ РЕШЕТКИ
1. Замените штатив 2 со щелью Щ на штатив с дифракционной решеткой ДР.
2. Установите экран Э так, чтобы на нем наблюдалась картина дифракции. Запишите в табл. 2 расстояние D от решетки до экрана.
Таблица 2
Номер опыта
|
D,
мм
|
k
|
Lk ,
мм
|
xk ,
мм
|
d,
мм
|
1
|
|
|
|
|
|
…
|
…
|
…
|
…
|
…
|
…
|
N
|
|
|
|
|
|
3. Отсчитайте от центра картины (среднего из трех наиболее ярких максимумов) влево и вправо по одинаковому количеству k главных максимумов (не считая центрального!); измерьте расстояние между ними Lk , как показано на рис. 4. Значения k иLk занесите в таблицу.
4. Повторите пп. 2 и 3, изменяя расстояние D от решетки до экрана так, чтобы общее число опытов n было не менее четырех.
5. Для каждого опыта по формулам (12) и (13) рассчитайте координату k-го максимума xk и период дифракционной решетки d. Результаты расчетов занесите в табл. 2.
6. Оцените среднее из измеренных значений 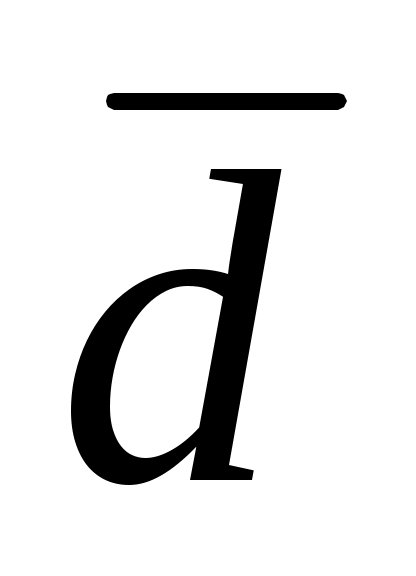 и запишите его в тетрадь. и запишите его в тетрадь.
Контрольные вопросы
Дифракция света. Принцип Гюйгенса-Френеля.
Метод зон Френеля и его применение для анализа дифракционной картины.
Дифракция Фраунгофера на одиночной щели. Условие наблюдения минимумов.
Дифракционная решетка. Период решетки. Характер дифракционной картины. Условия наблюдения главных максимумов и минимумов.
Дифракционная решетка как спектральный прибор. Угловая дисперсия и разрешающая способность решетки.
Литература:
[4] - §125-130; [8] - §5.1-5.9; [12] - §176-183.
|
 Скачать 1.84 Mb.
Скачать 1.84 Mb.





