МУ по Начертательной геометрии. МУ Начертательная геометрия и компьютерная графика. Методические указания по изучению дисциплины для обучающихся технических направлений всех форм обучения Составитель

• Название: Методические указания по изучению дисциплины для обучающихся технических направлений всех форм обучения Составитель
• Анкор: МУ по Начертательной геометрии
• Дата: 23.11.2021
• Размер: 0.75 Mb.
• Имя файла: МУ Начертательная геометрия и компьютерная графика.docx
• Тип: Методические указания; #279528
• страница: 4 из 4

Задача лист 3.
Построить фронтальную и горизонтальную проекции треугольников АВС и АСD и определить величину двугранного угла при ребре АС. Построить проекции отрезка прямой линии l, удаленной от плоскостей треугольников на расстоянии 15 мм. Данные для своего варианта взять из таблицы 2 или задание лист 3 распечатать на листе формата А4.

Для решения задачи необходимо изучить следующий теоретический материал:

- Точка и прямая. Образование чертежа точки в системе двух плоскостей проекций. Проекции отрезка прямой линии. Положение отрезка прямой относительно плоскостей проекций. Точка на прямой. Взаимное положение двух прямых.

- Плоскость. Различные способы задания плоскости на чертеже. Положение плоскости относительно плоскостей проекций.

- Способы преобразования чертежа. Способ замены плоскостей проекций.

Решение.

На листе формата А4 намечают оси координат (X,Y,Z). Из таблицы 3 согласно своего варианта строятся проекции точек А,В,С и D в горизонтальной и фронтальной плоскостях проекций. Точки А,С,В и А,С,D соединяем и получаем два треугольника, у которых АС общая сторона. Таким образом, плоскости двух треугольников образуют двугранный угол с общей стороной АС.

Двугранный угол проецируется в натуральную величину, если общая сторона АС будет расположена перпендикулярно плоскости проекций. Так как сторона АС является прямой общего положения, то необходимо, используя способ замены плоскостей проекций, прямую общего положения сначала преобразовать в прямую уровня, а затем прямую уровня преобразовать в проецирующую прямую, используя две замены плоскостей.

Вводим дополнительную плоскость проекций П₄ параллельно прямой АС. Проводим ось О₁Х₁ параллельно горизонтальной проекции прямой АС(А₁С₁) на небольшом расстоянии, выбранном произвольно. Проводим от горизонтальных проекций точек А₁В₁С₁D₁ линии проекционной связи перпендикулярно оси О₁Х₁ в плоскость П₄. На оси О₁Х₁ отмечаем точки А_Х1 В_Х1 С_Х1 D_Х1. Замеряем высоты точек АВСD в плоскости П₂ от оси ОХ по вертикальной линии проекционной связи до фронтальных проекций точек А₂ В₂ С₂ D₂ . Замеренные размеры высот откладываем от оси О₁Х₁ в плоскость П₄ по линиям проекционной связи и отмечаем точки А₄ В₄ D₄ C₄ . Так как высота точки С(С₂) равна 0 , то проекция точка С₄ будет расположена на оси О₁Х₁.

Вводим дополнительную плоскость проекций П₅ перпендикулярно АС на небольшом расстоянии, выбранном произвольно. Для этого продолжаем А₄C₄ и проводим ось проекций О₂Х₂ перпендикулярно А₄С₄. Проводим от точек В₄ D₄ линии проекционной связи перпендикулярно О₂Х₂ и на пересечении с осью отмечаем точки В_Х2 D_Х2 и А_Х2=В_Х2. Замеряем расстояние от оси О₁Х₁ до горизонтальных проекций точек А₁В₁С₁D₁ и замеренные размеры откладываем от оси О₂Х₂ и получаем проекции точек В₅ D₅ и А₅=С₅ , так как расстояние от оси О₁Х₁ до А₁С₁ одинаковое. Проекция двугранного угла в плоскости П₅ изображена в натуральную величину, так как плоскости треугольников АСВ и АСD стали перпендикулярны плоскости П₅.

Строим проекции отрезка прямой линии, удаленной от плоскостей треугольников на расстоянии 15 мм. Для этого проводим отрезки прямых параллельно А₅=С₅ , В₅ и параллельно А₅=С₅, D₅ на расстоянии 15 мм. Эти отрезки пересекаются в точке N₅. Через точку N₅ проводим прямую l₅ параллельную прямой А₅=С₅, которая проецируется на плоскости П₅ в точку N₅=l₅. Прямая l равноудалена от плоскостей треугольников АСВ и АСD на расстоянии 15 мм. и перпендикулярна плоскости проекций П₅.

Строим проекцию прямой l(l₄) в плоскости П₄.

Проводим от точки N₅= l₅ линию проекционной связи в плоскость П₄ перпендикулярно оси О₂Х₂ и на этой линии проекционной связи отмечаем точку N₄ произвольно в любом месте. Обводим линию l₅ с учетом видимости. Видимой она будет только там, где она выходит за изображение плоскости треугольника АСD.
Таблица 3

№вар.	XA	YA	ZA	XB	YB	ZB	XC	YC	ZC	XD	YD	ZD
	19	30	24	72	12	80	102	70	0	42	80	65
	18	66	40	55	12	72	96	30	18	84	56	66
	96	38	18	48	6	78	12	60	48	68	62	62
	18	40	14	65	10	74	102	64	44	38	76	68
	30	34	12	72	60	12	102	0	72	30	60	55
	40	68	16	90	30	70	0	10	45	17	66	80
	55	72	30	5	24	6	78	30	84	35	70	65
	18	36	18	66	6	78	102	60	48	38	72	72
	96	36	72	72	12	24	30	78	48	96	60	40
	55	6	66	102	60	12	24	30	0	30	60	55
	102	34	12	48	60	12	18	0	72	90	60	55
	55	30	64	6	54	18	84	24	6	84	71	59
	18	24	30	72	60	12	102	0	72	42	66	60
	72	6	66	108	72	45	42	44	0	55	66	50
	102	24	30	48	60	12	18	0	72	78	66	60
	55	22	72	6	6	24	78	78	57	40	65	65
	55	6	66	6	66	12	84	30	0	84	50	43
	102	12	24	48	12	60	22	72	0	90	55	60

Строим проекцию прямой l в плоскости П₁ рис.21.

Проводим от точки N₄ линию проекционной связи в плоскость П₁ перпендикулярно оси О₁Х₁ . На пересечении с осью О₁Х₁ отмечаем точку N_X1 и от этой точки откладываем расстояние, замеренное от точки N_X2 до точки N₅=l₅ . Получаем горизонтальную проекцию точки N(N₁). Через точку N₁ проводим горизонтальную проекцию прямой l( l₁) с учетом видимости. Видимой прямая l(l₁) в горизонтальной плоскости проекций будет там, где она выходит за изображение треугольника АСD(A₁C₁D₁).

Строим проекцию прямой l в плоскости П₂.

Проводим от точки N₁ линию проекционной связи вверх перпендикулярно оси ОХ и на пересечении с осью ОХ отмечаем точку N_X Замеряем расстояние от точки N_X1 до точки N₄ в плоскости П₄ и откладываем от точки N_X вверх и получаем фронтальную проекцию точки N(N₂). Проводим через точку N₂ линию l(l₂) параллельно А₂С₂ с учетом видимости .

Образец оформления работы показан в приложении 4.

Задача лист 4
Построить линию пересечения четырёхугольной призмы и треугольной пирамиды.

Данные для своего варианта взять из таблицы 3 или лист 4 распечатать на листе формата А4.

Для решения задачи необходимо изучить следующие теоретический материал:

- проецирование многогранных поверхностей на комплексном чертеже;

- построение линии пересечения многогранных поверхностей с проецирующей плоскостью;

- определение видимости линии пересечения многогранных поверхностей.
Решение

Для решения на листе формата А4 намечают оси координат (X,Y,Z). Из таблицы 4 согласно своему варианту строятся очерки поверхностей четырехугольной призмы и треугольной пирамиды. Боковые грани призмы являются плоскостями горизонтально-проецирующими, то есть перпендикулярными горизонтальной плоскости проекций. Линия пересечения многогранных поверхностей — это ломаная линия. Отмечаем точки пересечения грани UG (U₁G₁) c ребрами пирамиды на горизонтальной плоскости проекций.

Ребро AD(A ₁D₁) BD(B₁D₁) CD(C₁D₁) соответственно пересекаются с гранью призмы UG (U₂G₂) в точках 1₁, 2₁, 3₁. Находим фронтальные проекции полученных точек. Для этого проведём вверх вертикальные линии связи до пересечения с фронтальными проекциями соответствующих рёбер пирамиды и получаем фронтальные проекции точек 1₂ , 2₂ , 3₂ на ребрах A₂D₂, B₂D₂, C₂D₂. Обводим учетом видимости линию пересечения. Линию от точки 1₁ до точки 2₁ обводим штриховой линией невидимого контура, так как грань ABD во фронтальной плоскости проекций является невидимой, соответственно и линия пересечения 1₁2₁, принадлежащая грани АВD, тоже является невидимой .

На горизонтальной плоскости проекций отмечаем линию пересечения плоскости EG(E₁,G₁) с гранями и рёбрами треугольной пирамиды.

Точки 4(4₁) и 5(5₁) являются точками пересечения грани EG(E₁,G₁) с рёбрами пирамиды AD(A₁,D₁) и CD(C₁,D₁). Находим фронтальные проекции точек 4 и 5. Проводим вверх вертикальные линии связи до пересечения с фронтальными проекциями ребер пирамиды и получаем фронтальные проекции точек 4₂ и 5₂ на рёбрах AD(A₂,D₂) и СD(C₂,D₂).

Ребро призмы ЕЕ является горизонтально –проецирующей прямой, поэтому это ребро пересекает грань BCD(B₁,C₁ D₁) в точке 6(6₁ ) и грань ABD (A₁,B₁D₁) в точке 8(8₁). Поэтому на горизонтальной плоскости проекций проекция ребра призмы ЕЕ(Е₁) и проекции точек пересечения с рёбрами пирамиды совпадают Е₁=6₁ =8₁ .
Таблица 4

№вар.	XA	YA	XB	YB	XC	YC	XD	YD	XE	XK	XG	XU
	141	75	122	14	87	100	0	50	100	74	16	55
	0	70	20	9	53	95	141	45	40	67	125	86
	0	80	20	19	53	110	141	55	40	67	125	86
	0	68	20	7	53	93	141	43	40	67	125	86
	0	75	20	14	53	100	141	50	40	67	125	86
	0	82	20	21	53	112	141	57	40	67	125	86
	0	85	20	24	53	115	141	60	40	67	125	86
	0	90	20	29	53	120	141	65	40	67	125	86
	0	85	15	30	55	120	141	60	40	67	125	86
	141	70	122	9	87	95	0	45	100	74	16	55
	141	80	122	19	87	110	0	55	100	74	16	55
	141	68	122	7	87	93	0	43	100	74	16	55
	141	82	122	21	87	112	0	57	100	74	16	55
	141	85	122	24	87	115	0	60	100	74	16	55
	141	90	122	29	87	120	0	65	100	74	16	55
	135	75	116	14	81	100	0	50	100	74	16	55
	145	75	126	14	91	100	0	50	100	74	16	55
	145	95	120	34	87	120	0	70	100	74	16	55

Z_A=Z_E=Z_K=Z_G=Z_U=0; Z_C=Z_D=40; Y_E=50 Y_K=Y_G=20; Z_В=60; Y_U=95;

высота призмы h=85.

Находим фронтальную проекцию точки 6(6₂). Для этого на горизонтальной плоскости проекций через точку Е₁=6₁=8₁ проводим линию от точки D₁ до пересечения с ребрами B₁,C₁ и отмечаем точку N₁. Для нахождения фронтальной проекции линии DN (D₂,N₂) от точки N₁ проводим вверх вертикальную линию связи до пересечения с ребром B₂,С₂ и полученную точку N₂ соединяем с точкой D₂. На пересечении с ребром призмы Е (Е₂Е₂) получаем точку 6₂ .

Аналогично находим точку 8.

Для этого проводим через точку Е₁=6₁=8₁ и вершину пирамиды D(D₁) линию до пересечения с ребром AB(A₁ B₁) и получаем точку М(М₁). Находим фронтальную проекцию точки М(М₂), соединяем её с вершиной пирамиды D (D₂) и на пересечение с ребром призмы ЕЕ получаем точку 8₂.

Пересечение грани призмы ЕК (Е₁К₁) с ребром ВD (B₁D₁) и на пересечении ставим точку 7(7₁). Находим фронтальную проекцию точки 7(7₂) по принадлежности ребру BD(B₂,D₂).

Соединяем последовательно точки 4-8 линии пересечения многогранников с учетом видимости.

Видимыми на фронтальной плоскости проекций являются грани пирамиды АСD(A₂C₂D₂) и ВСD(В₂С₂D₂) и грани призмы EG(E₂G₂). Поэтому линия пересечения от точки 4₂ до 5₂ , от точки 5₂ до 6₂ во фронтальной плоскости проекций будут видимыми, а линии от точки 4₂ до 8₂ , от точки 8₂ до 7₂ , от точки 7₂ до 6₂ будут невидимыми.

СПИСОК ЛИТЕРАТУРЫ

1. Технология бурения нефтяных и газовых скважин: учебник для студентов вузов - в 5 т. Т.5. /под общей редакцией В.П. Овчинников. - Тюмень: ТИУ, 2017.-312 с.

2. Особенности добычи нефти и газа из горизонтальных скважин [Текст]: учебное пособие / Г.П. Зозуля [и др.]; под ред. Г.П. Зозули.- М.: Изд. Центр «Академия», 2009. - 176 с.

3. Техника и технология строительства боковых стволов в нефтяных и газовых скважинах [Текст]: учебное пособие / В.М. Шенбергер [и др.].- Тюмень: Изд-во «ЦентрЛитНефтегаз», 2007.- 496 с.

4. Исследование скважин по КВД / Р.Г. Шагиев. М.: Изд. Наука, 1998.- 304с.

5. Гидродинамические исследования малодебитных нефтяных скважин./ А.К. Ягафаров и др. Изд. Вектор Бук, 2006.-349с.

Приложение 1


Приложение 2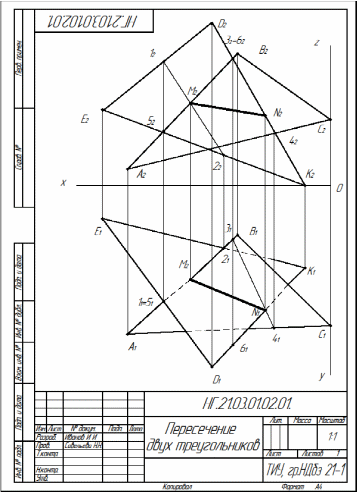



Приложение 3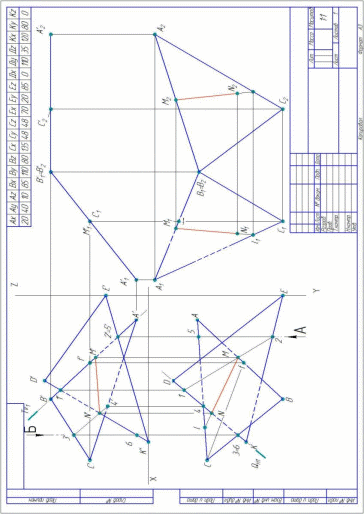



Приложение 4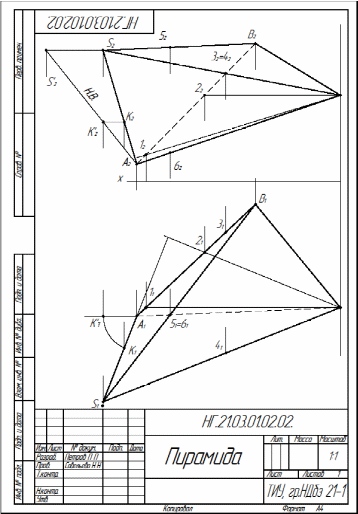



Приложение 5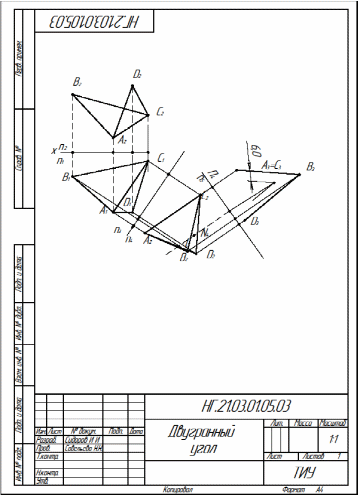
Приложение 6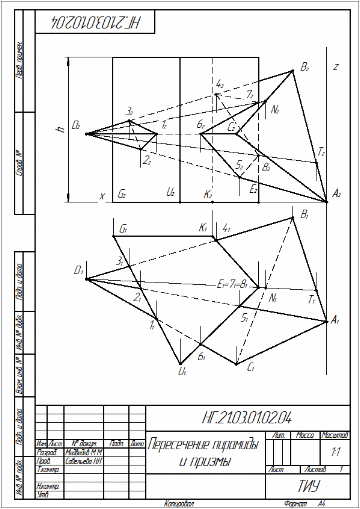

СПИСОК ЛИТЕРАТУРЫ

1. Технология бурения нефтяных и газовых скважин: учебник для студентов вузов - в 5 т. Т.5. /под общей редакцией В.П. Овчинников. - Тюмень: ТИУ, 2017.-312 с.

2. Особенности добычи нефти и газа из горизонтальных скважин [Текст]: учебное пособие / Г.П. Зозуля [и др.]; под ред. Г.П. Зозули.- М.: Изд. Центр «Академия», 2009. - 176 с.

3. Техника и технология строительства боковых стволов в нефтяных и газовых скважинах [Текст]: учебное пособие / В.М. Шенбергер [и др.].- Тюмень: Изд-во «ЦентрЛитНефтегаз», 2007.- 496 с.

4. Исследование скважин по КВД / Р.Г. Шагиев. М.: Изд. Наука, 1998.- 304с.

5. Гидродинамические исследования малодебитных нефтяных скважин./ А.К. Ягафаров и др. Изд. Вектор Бук, 2006.-349с.

Учебное издание

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ И ИНЖЕНЕРНАЯ (КОМПЬЮТЕРНАЯ) ГРАФИКА

Часть I

Методические указания по изучению дисциплины для обучающихся

технических направлений всех форм обучения
Составитель

САВЕЛЬЕВА Наталия Николаевна

В авторской редакции

Подписано в печать . Формат 60х90 1/16. Усл. печ. л. 2,875.

Тираж экз. Заказ № .

Библиотечно-издательский комплекс

федерального государственного бюджетного образовательного учреждения высшего образования

«Тюменский индустриальный университет».

625000, Тюмень, ул. Володарского, 38.
Типография библиотечно-издательского комплекса.

625039, Тюмень, ул. Киевская, 52.