МУ для заочников Основы электротехники. Методические указания по изучению дисциплины и выполнению контрольных заданий для учащихся заочников 3 курса
 Скачать 1.07 Mb. Скачать 1.07 Mb.
|
|
Пример 5. В трехфазную четырехпроводную сеть включены звездой лампы накаливания мощностью Р = 300 Вт каждая. В фазу А включили 30 ламп, в фазу В - 50 ламп и в фазу С - 20 ламп. Линейное напряже ние сети Uном = 380 В (рис. 5, а). Определить токи в фазах и начертить векторную диаграмму цепи, из которой найти числовое значение тока в нулевом проводе. Решение. 1. Определяем фазные напряжения установки: UA = UB = UC = Uном / 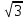 = 380/1,73 = 220В. = 380/1,73 = 220В.2. Находим фазные токи: IA = PФА / UА = 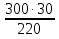 = 41 А; = 41 А;IB = PФB / UB =  = 68 А; = 68 А;IC = PФC / UC =  = 27,3 А. = 27,3 А.3. Для построения векторной диаграммы выбираем масштабы по току: 1 см - 20 А и по напряжению: 1 см - 80 В. Построение диаграммы начинаем с векторов фазных напряжений UA, UB, UC (рис - 5, б), располагая их под углом 120° друг относительно друга. Чередование фаз обычное: за фазой А - фаза В, за фазой В - фаза С. Лампы накаливания являются активной нагрузкой, поэтому ток в каждой фазе совпадает с соответствующим фазным напряжением. В фазе А ток IA = 41 А, поэтому на диаграмме он выразится вектором, длина которого равна 41/20=2,05 см. Длина вектора фазного напряжения UA составит 220/80 = 2,75 см. Аналогично строим векторы токов и напряжений в остальных фазах. Ток I0 в нулевом проводе является геометрической суммой всех фазных токов. Измеряя длину вектора тока I0 в нулевом проводе, получаем 1,75 см, поэтому I0 = 1,75-20=35 А. Векторы линейных напряжений на диаграмме не показаны, чтобы не усложнять чертеж. Пример 6. В трехфазную четырехпроводную сеть включили звездой несимметричную нагрузку: в фазу А - конденсатор с емкостным сопротивлением хА= 10 Ом; в фазу В - активное сопротивление RB = 8 Ом и индуктивное хB= 6 Ом, в фазу С - активное сопротивление Rс = 5 Ом. Линейное напряжение сети Uном = 380 В. Определить фазные токи, начертить в масштабе векторную диаграмму цепи и найти графи чески ток в нулевом проводе. Схема цепи дана на рис.6,а.  Решение. 1. Определяем фазные напряжения установки UA = UB = UC = Uном / 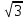 = 380/1,73 = 220В. = 380/1,73 = 220В.2. Находим фазные токи: IA = UА / xА =  = 22 А; = 22 А;IB = UB / zB =  = 22 А; = 22 А;Здесь zB =  = UC / RC = 220/5 = 44 A. Для построения векторной диаграммы выбираем масштабы по току: 1 см - 10 А и по напряжению: 1 см - 100 В. Построение диаграммы на чинаем с векторов фазных напряжений UA , UB , UC, располагая их под углом 120° друг относительно друга (рис. 6, б). Ток IA опережает на пряжение UАна угол 90°; ток IA отстает от напряжения UB на угол φB, который определяется из выражения cos φB = 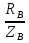 = = = 0,8; φB = 36°50'. = 0,8; φB = 36°50'. Ток IC совпадает с напряжением UC. Ток в нулевом проводе равен гео метрической сумме трех фазных токов. Измеряя длину вектора тока I0, которая оказалась равной 6,8 см, находим ток I0 = 68 А.  Пример 7. По заданной векторной диаграмме для трехфазной цепи (рис. 7, а) определить характер нагрузки каждой фазы и вычислить ее сопротивление. Начертить соответствующую схему цепи. Нагрузка включена в звезду. Определить активную и реактивную мощности, по требляемые цепью. Значения напряжений, токов и фазных углов приве дены на диаграмме. Векторы линейных напряжений не показаны. Решение. 1. Рассматривая векторную диаграмму, можно заме тить, что ток в фазе А отстает от фазного напряжения UA на угол φA = 53°10', значит в фазу A включена катушка с полным сопротивлением zА= UА/IA = 220/22=10Ом. Ее активное и индуктивное сопротивления вычисляем по формулам RA = zА cos φA = 10 соs 53о10' = 10 · 0,6 = 6 Ом; xA = zА sin φA = 10 sin 53о10' = 10 · 0,8 = 8 Ом; В фазе В ток IA совпадает с напряжением UB, значит в фазу В включено активное сопротивление RB=UB/IB = 220/11 = 20 0м. В фазе С ток IC опережает напряжение UCна угол φC = - 36°50', значит в фазу С включены конденсатор и активное сопротивление, Пол ное сопротивление фазы zC = UC/IC = 220/44 = 5Ом. Определим активное и емкостное сопротивления: RC = zC cos φC = 5 соs 36о50' = 5 · 0,8 = 4 Ом; xC = zC sin φC = 5 sin 36о50' = -5 · 0,6 = - 3 Ом; Схема цепи приведена на рис. 7, б. 2. Определяем мощности, потребляемые цепью. Активная мощность P = PA + PB + PC =  RA + RA +  RB + RB + 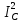 RC = 222 · 6 +112 · 20 + 442 · 4 = 13 068 Вт = 13,068 кВт. RC = 222 · 6 +112 · 20 + 442 · 4 = 13 068 Вт = 13,068 кВт. Реактивная мощность Q = QA - QC =  xA - xA - 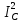 xC = 222 · 8 -442 · 3 = - 9680 вар = - 9,68 квар. xC = 222 · 8 -442 · 3 = - 9680 вар = - 9,68 квар.Знак минус показывает, что в цепи преобладает емкость. Пример 8. В трехфазную сеть включили треугольником несимметричную нагрузку (рис. 8, а) в фазу АВ - конденсатор с емкостным сопротивлением xAB = 10 Ом; в фазу ВС - катушку с активным сопротивлением RBC = 4 Ом и индуктивным xBC=3 Ом; в фазу СА - активное сопротивлениеRCA- 10 Ом. Линейное напряжение сети UНОМ = 220 В.  Определить фазные токи, углы сдвига фаз и начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить числовые значения линейных токов. Решение 1. Определяем фазные токи и углы сдвига фаз: IAB = UНОМ/xAB = 220/10 = 22А; φAB = - 90°; IBC = 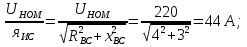 cos φBC = RBC/zBC = 4/5 = 0,8, где zBC = 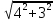 = 5 ОМ. = 5 ОМ.Отсюда угол φBC = 36°50'. Iса= Uном/RCA = 220/10 = 22 А; φCA = 0. Для построения векторной диаграммы выбираем масштаб по току: 1 см - 10 А, по напряжению: 1 см - 80 В. Затем в принятом масштабе откладываем векторы фазных (они же линейные) напряжений UAB, UBC, UCА, под, углом 120° друг относительно друга (рис. 8, б). Под уг лом φав= -90° к вектору напряжения Uав откладываем вектор тока IАВ; в фазе ВС вектор тока IВС. должен отставать от вектора напряжения UBCна угол φBC = 36°50', а в в фазе СА вектор тока IАC совпадает с вектором напряжения Uса. Затем строим векторы линейных токов на основании известных уравнений IA = IAB – ICA = IAB + ( - ICA); IB = IBC + ( - IAB); IC = ICA + ( - IBC). Измеряя длины векторов линейных токов и пользуясь принятым масштабом, находим значения линейных токов: IА = 11 А; IВ = 57А; IC = 47 А. Пример 9. По векторной диаграмме для трехфазной цепи (рис. 9, а) определить характер нагрузки в каждой фазе, вычислить ее сопротивление и начертить схему включения. 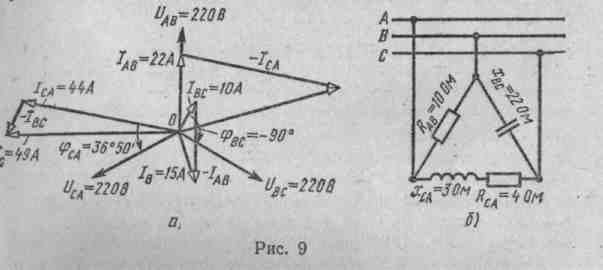 Нагрузка несимметричная, соединена в треугольник. Значения напряжений, фазных токов и углов сдвига фаз указаны на диаграмме. Решение. 1. Рассматривая векторную диаграмму, можно заключить, что ток IABв фазе АВ совпадает с напряжением Uав, значит в фазу АВ включено активное сопротивление Rав = Uав/Iав = 220/22 =10 Ом. В фазе ВС ток IBCопережает напряжение на угол φBC = -90°, значит в фазу ВС включено емкостное сопротивление xBC = UAB/IAB= 220/10 = 22 Oм В фазе СА ток IСАотстает от напряжения UCAна угол φCA =36о50', значит в фазу СА включено активно-индуктивное сопротивление zCA = UCA/ICA = 220/44 = 5 Ом. Очевидно, RCA = zCA cos φCA = 5 соs 36о50' = 5 · 0,8 = 4 Ом; xCA = zCA sin φCA = 5 sin 36о50' = 5 · 0,6 = 3 Ом; 2. На основании вычислений чертим схему цепи (рис. 9, б). Пример 10. В трехфазную четырехпроводную сеть включены печь сопротивления, представляющая собой симметричную нагрузку, соединенную треугольником, и несимметричная осветительная нагрузка) в виде ламп накаливания, соединенных звездой (рис. 10, а). Мощность каждой фазы печи Рп - 10 кВт. Мощность каждой лампы Рл=200 Вт  число ламп в фазах nA =50; nB = 40; nC = 30. Номинальное напряжение сети Uном = 380 В. Определить показания всех приборов, включенные в схему. Решение. 1. Находим фазные токи, потребляемые печью:. IAB = IBC = ICA = Pn /Uном = 10 · 1000 /380 = 26,3 А. Таким образом, амперметр АIпокажет силу тока 26,3 А.
IA =  = 45,4 A; = 45,4 A;IB =  = 36,4 A; = 36,4 A;IC =  = 27,3 A; = 27,3 A;Амперметры АЗ, А4, А5, включенные в линейные провода, соответствен но покажут эти токи. 4. Для определения тока в нулевом проводе I0 начертим в масштабе векторную диаграмму цепи, где включены лампы, Выбираем масштаб для напряжений и токов: 1 см - 100 В; 1 см - 10 А. Затем в принятом масштабе откладываем векторы фазных напряжений UA, UB, и UC, располагая их под углом 120° друг относительно друга (рис. 10, б). Чередование фаз обычное: за фазой А - фаза В, за фазой В - фаза С. I Лампы накаливания являются активной нагрузкой, поэтому ток в каждой фазе совпадает с соответствующим фазным напряжением. В фа зе А ток IA =45,4 А, поэтому на диаграмме он выразится вектором, дли на которого равна 45,4 : 10=4,54 см; длина вектора фазного напряжения UАсоставит: 220 : 100=2,2 см. Аналогично строим векторы токов и напряжений в остальных фазах. Ток I0 в нулевом, проводе определяется геометрической суммой всех трех фазных токов. Измеряя длину векто ра тока I0, которая оказалась равной 1,5 см, получим значение тока в нулевом проводе I0= 15 А. Векторы линейных напряжений на диаграмме не показаны, чтобы не усложнять чертеж. Контрольная работа Задание 1 Задача 1 (варианты 01-00). Цепь постоянного тока содержит несколько резисторов, соединенных смешанно. Схема цепи с указанием сопротивлений резисторов приведена на соответствующем рисунке. Номер рисунка, заданные значения одного из напряжений или токов и ве личина, подлежащая определению, приведены в табл. 3. Всюду индекс тока или напряжения совпадает с индексом резистора, по которому про ходит этот ток или на котором действует это напряжение. Например, через резистор R3 проходит ток I3 и на нем действует напряжение U3. Определить также мощность, потребляемую всей цепью, и расход элект рической энергии цепью за 8 ч работы. Пояснить с помощью логических рассуждений характер изменения электрической величины, заданной в таблице вариантов (увеличится, уменьшится, останется без изменения), если один из резисторов замк нуть накоротко или выключить из схемы. Характер действия с резисто ром и его номер указаны в табл. 3. При этом считать напряжение UABнеизменным. При трудностях логических пояснений ответа можно вы полнить расчет требуемой величины в измененной схеме и на основании сравнения ее в двух схемах дать ответ на вопрос. Указание. См. решение типового примера 1. Задача 2 (варианты 01-50). Цепь переменного тока содержит различные элементы (резисторы, индуктивности, емкости), включенные последовательно. Схема цепи приведена на соответствующем рисунке. Номер рисунка и значения сопротивлений всех элементов, а также один дополнительный параметр заданы в табл. 4. Начертить схему цепи и определить следующие величины, относящиеся к данной цепи, если они не заданы в табл. 4: 1) полное сопротив ление г; 2) напряжение U, приложенное к цепи; 3) ток I; 4) угол сдвига фаз φ (по величине и знаку); 5) активную Р, реактивную Q и полную S мощности цепи. Начертить в масштабе векторную диаграмму цепи и пояснить ее построение. С помощью логических рассуждений пояснить характер изменения (увеличится, уменьшится, останется без изменения) тока, активной, реактивной мощности в цепи при увеличении частоты тока в два раза, Напряжение, приложенное к цепи, считать неиз менным.    таблица 3
| ||||||||||||||||
