|
|
Методич_стат-исправлено. Методические указания по курсу Информатика
Контрольные вопросы
Метод Эйлера
Что является решением дифференциального уравнения?
Необходим ли поиск начальных условий в методе Эйлера?
К какой группе относится модифицированный метод Эйлера?
Почему точность метода Эйлера пропорциональна h, а модифицированного — h2?
Метод Эйлера относится к одно шаговым методам. В чем основное отличие одно- и многошаговых методов?
Можно ли методом Эйлера решать системы дифференциальных уравнений?
Можно ли использовать метод Эйлера для решения задач, не относящихся к задачам Коши?
Обязательно ли необходимо задание начальных условий при решении дифференциального уравнения методом Эйлера?
В чем заключается отличие явных и неявных вычислительных схем в модифицированном методе Эйлера?
Можно ли оценить погрешность решения дифференциального уравнения, не зная точного решения?
Метод Рунге — Кутта
Сколько раз необходимо на каждом шаге вычислять правую часть уравнения при использовании метода четвертого порядка?
Как можно оценить погрешность решения дифференциального уравнения при использовании метода Рунге — Кутта?
Можно ли задавать погрешность решения при автоматическом подборе шага в относительных величинах?
Сколько предыдущих значений функции нужно иметь, чтобы сосчитать одно следующее значение?
К какой группе методов (аналитические или численные) относится имеющий аналитическое выражение от искомого значения функции метод Рунге — Кутта?
Как записывается рекуррентная формула метода четвертого порядка?
Что можно отнести к недостаткам метода, например, самого распространенного четвертого порядка?
Как зависит погрешность метода от величины шага решения?
Возможно ли применение переменного шага в методе Рунге — Кутта?
Варианты заданий к лабораторной работе
№
п/п
|
Уравнение
|
Начальные
значение
|
Конечное значение
|
Шаг
|
Начальное значение функции Y
|
|
Y' = y + e2x
|
0
|
1,5
|
0.16
|
Y(0)=3
|
|
Y' = cos(x) - y
|
0
|
2
|
0.2
|
Y(0)=1.5
|
|
Y' = 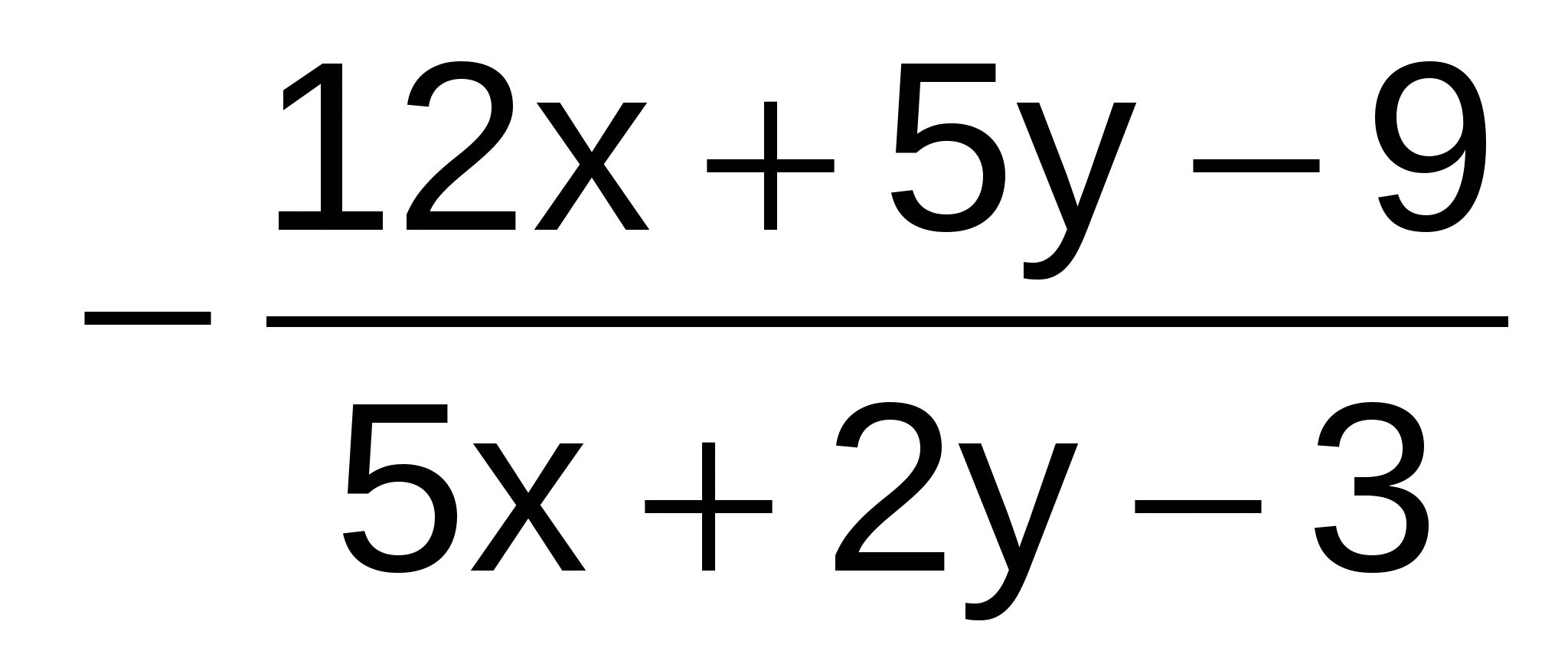
|
0
|
2
|
0,2
|
Y(0)=0
|
|
Y' = x2 - 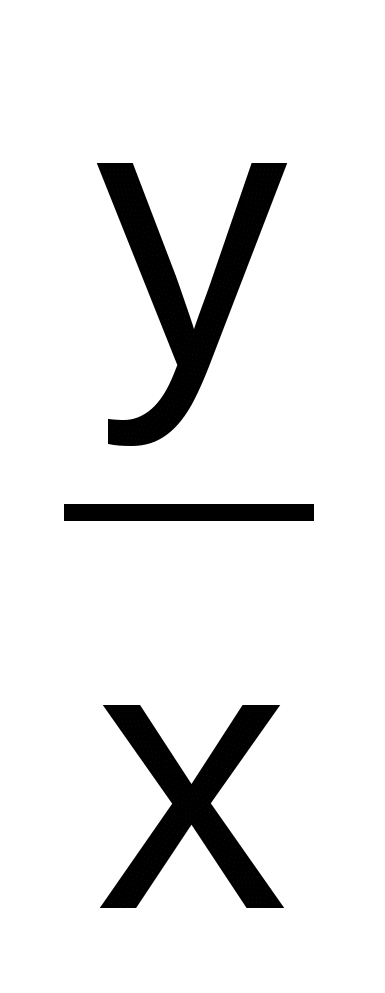
|
1
|
3
|
0,2
|
Y(1)=1
|
|
Y' = e2x - 3y
|
0
|
2
|
0,2
|
Y(0) = 0
|
|
Y' = 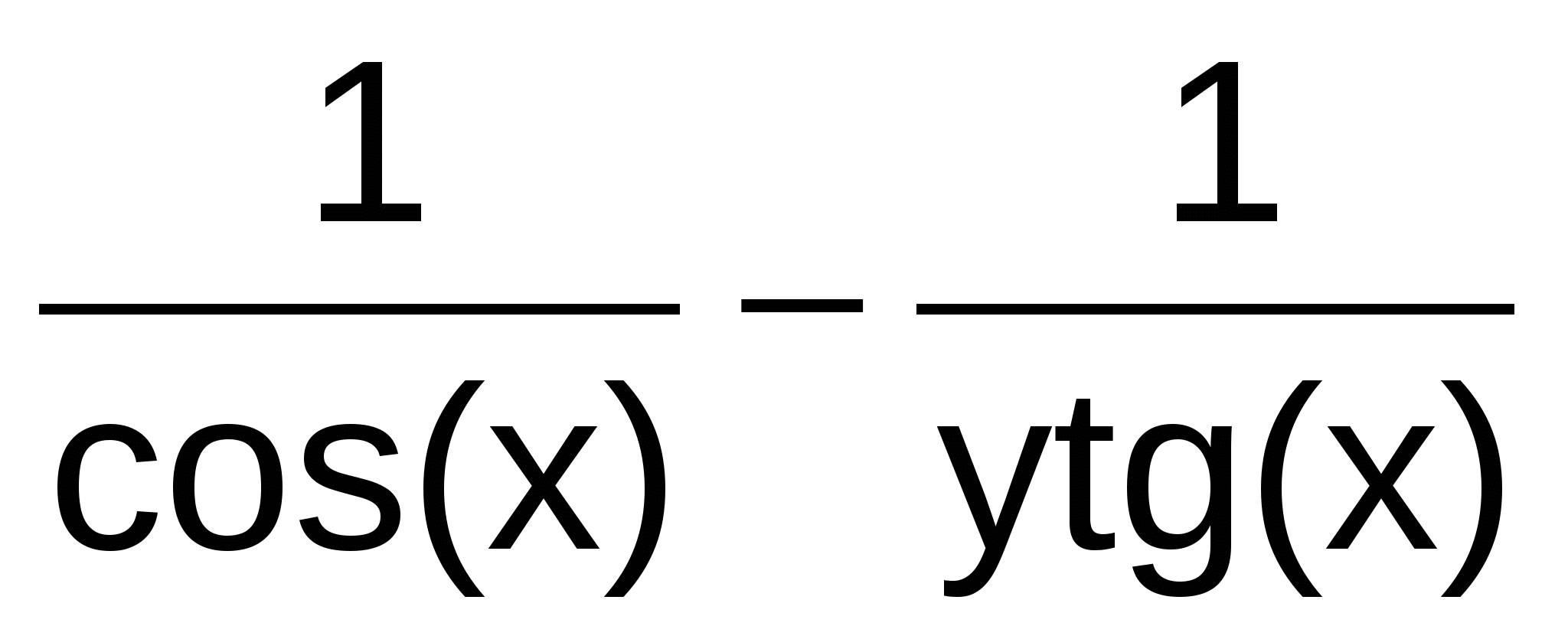
|
0
|
2
|
0,2
|
Y (0) = 2
|
|
Y' = ex – x + 2y
|
0
|
2
|
0,2
|
Y (0) = 0
|
|
Y' = 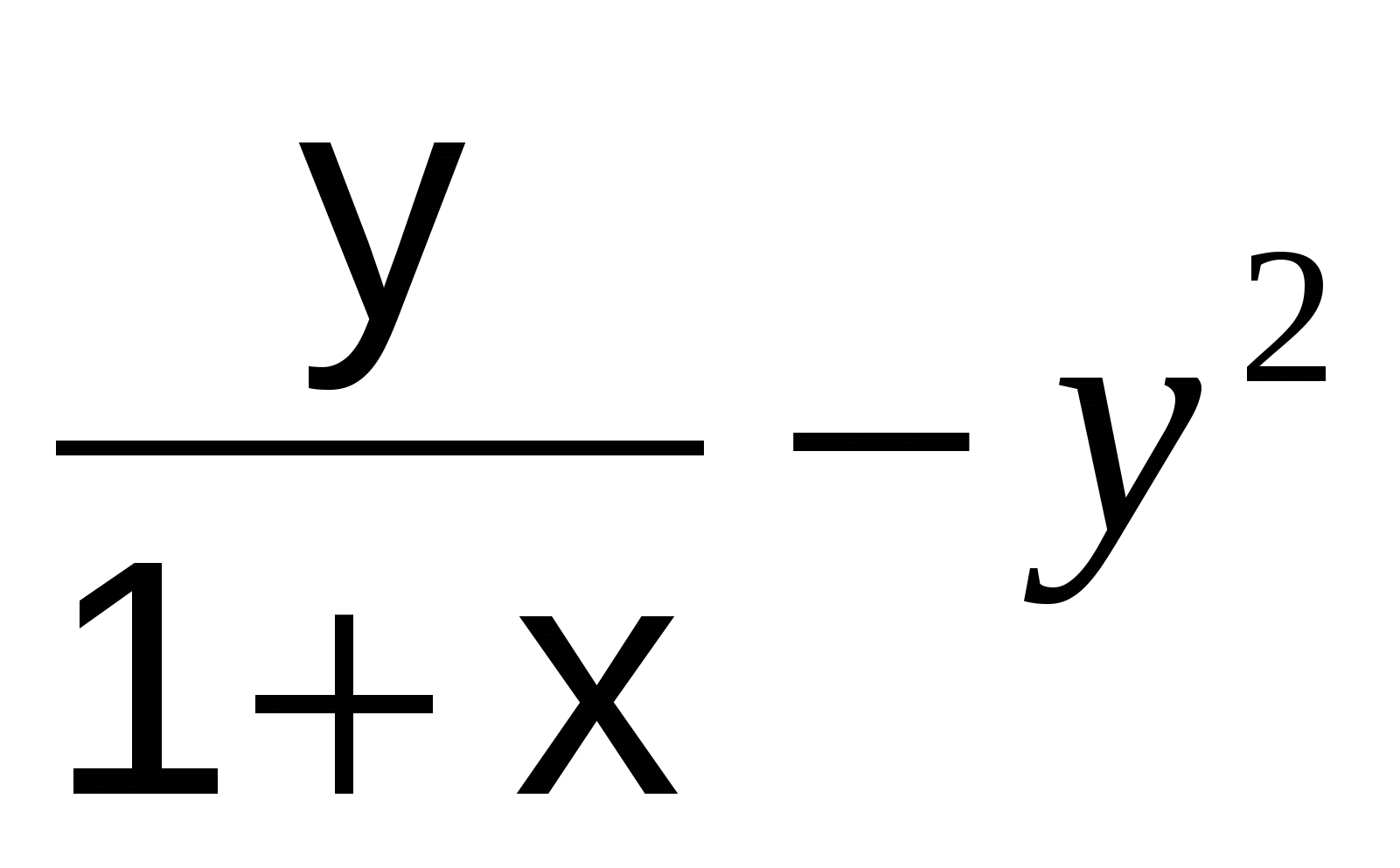
|
0
|
2
|
0,2
|
Y (0) = 1
|
|
Y' = 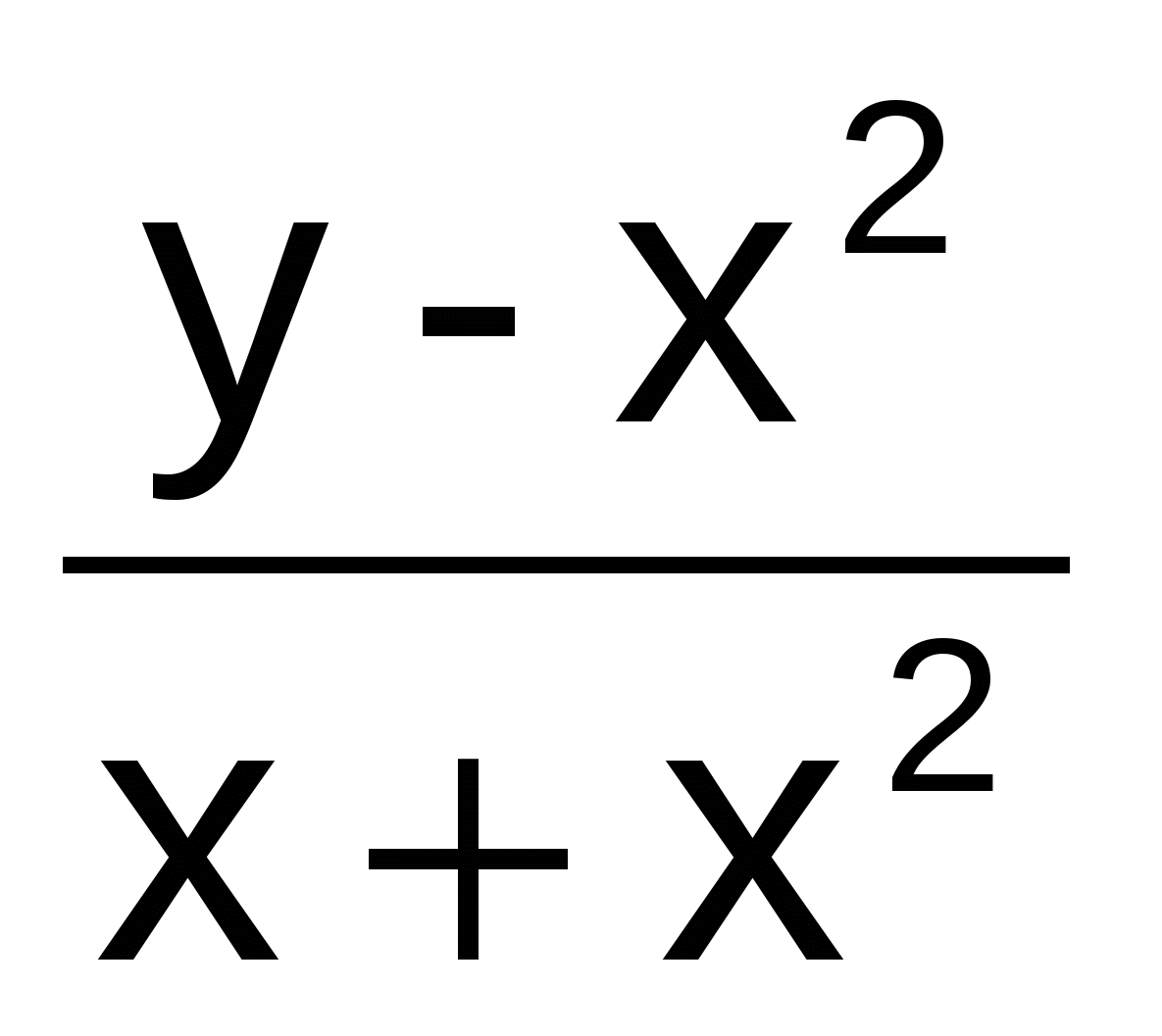
|
1
|
3
|
0,2
|
Y (1)=1
|
|
Y' = -4y + sin(2x)
|
0
|
1
|
0,2
|
Y(0) = 1
|
|
Y' = -y + e-xcos(x)
|
0
|
2
|
0,1
|
Y(0) = 0
|
|
Y' = -y + 1-ex
|
0
|
2
|
0,2
|
Y(0) = 2,5
|
|
Y' = -y + excos(x)
|
0
|
1
|
0,2
|
Y(0) = 0
|
|
Y' = -y – sin(xex)
|
0
|
2
|
0,1
|
Y(0) = 1
|
|
Y' = xy
|
0
|
1
|
0,2
|
Y(0) = 1
|
|
Y' = x+ 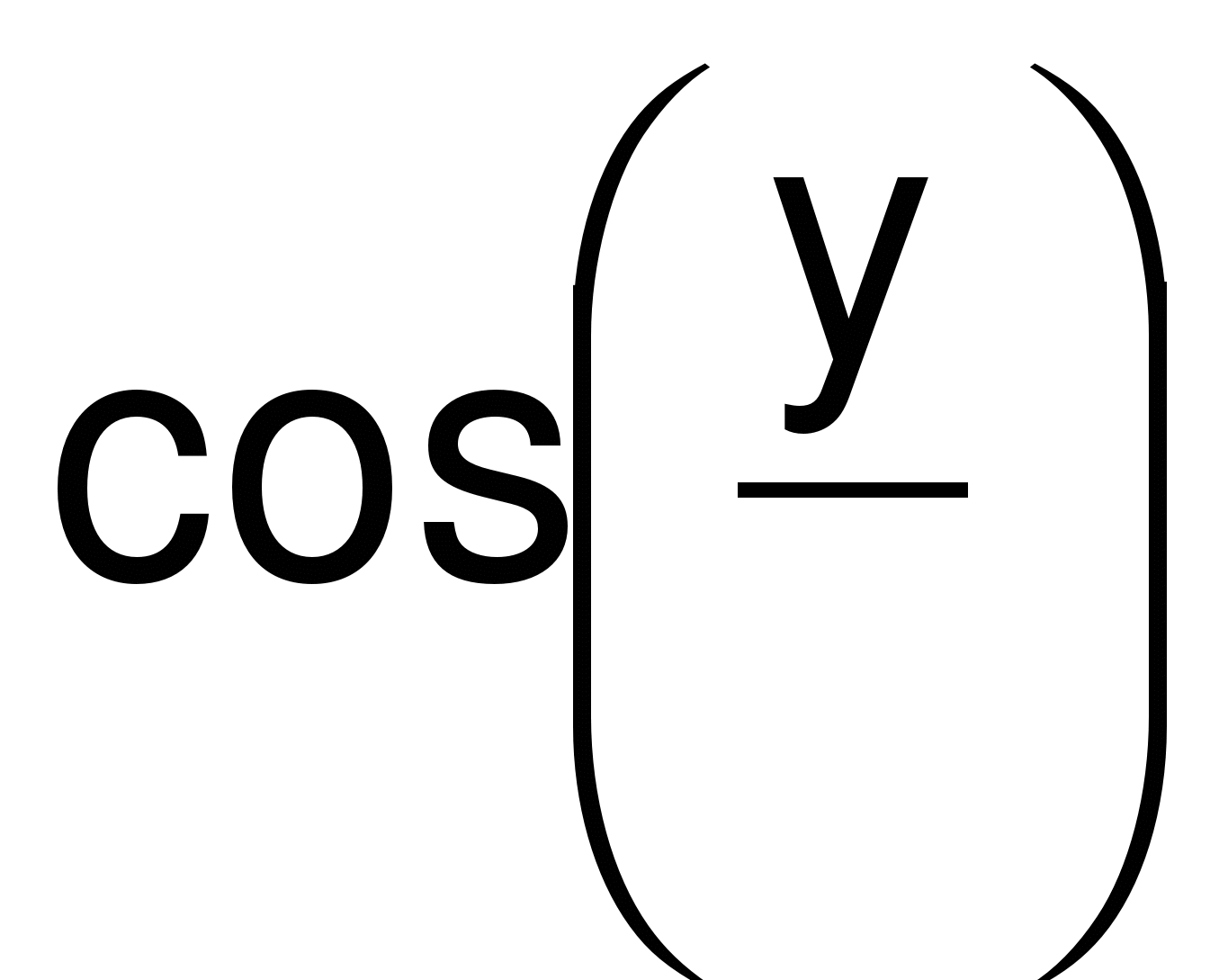
|
1,7
|
3
|
0,1
|
Y0(1,7) = 5,3
|
|
Y' =  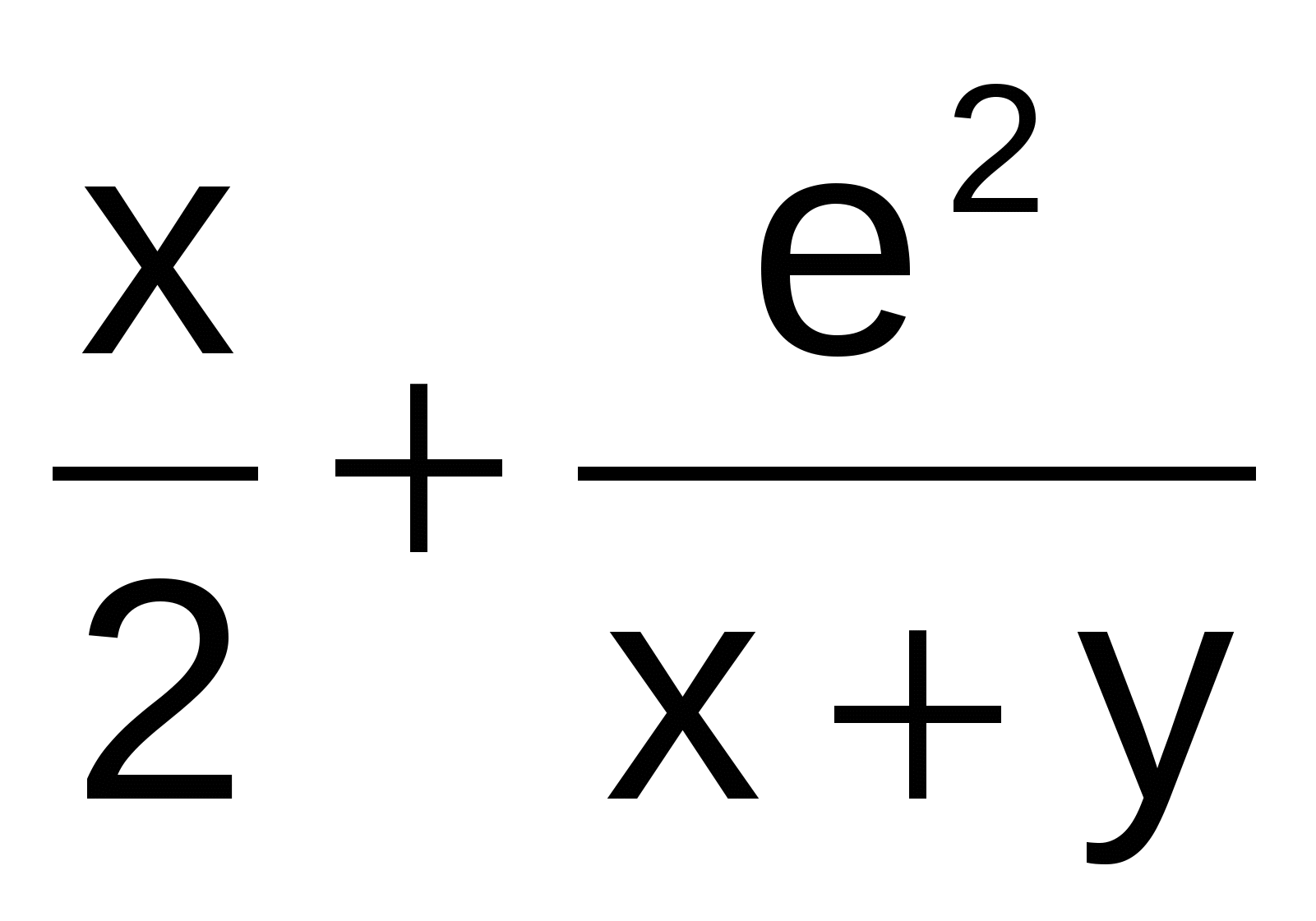
|
1,8
|
2,5
|
0,15
|
Y0(1,3) = 4,5
|
|
Y' = 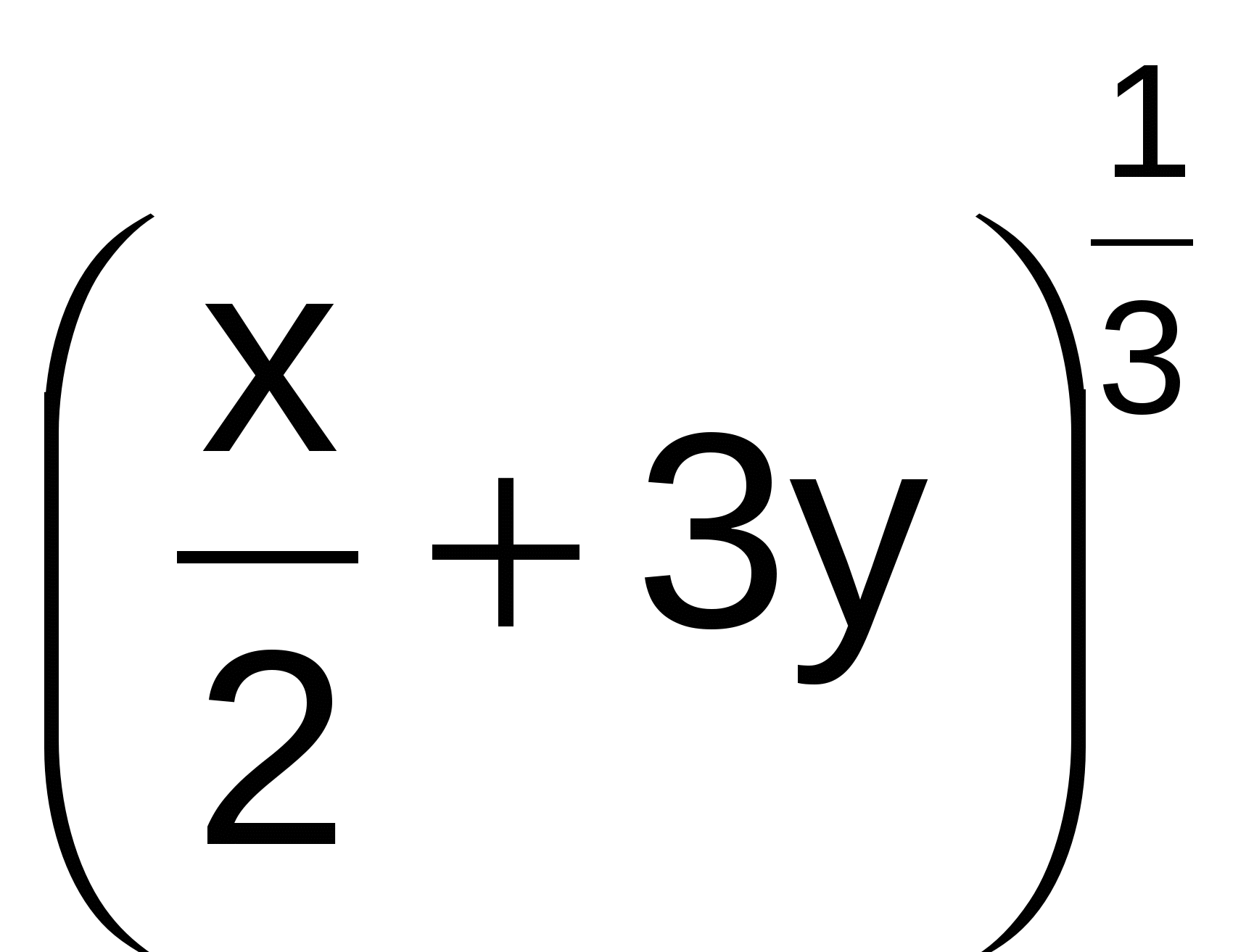
|
3,1
|
5,4
|
0,1
|
Y0(3) = 5
|
|
Y' = 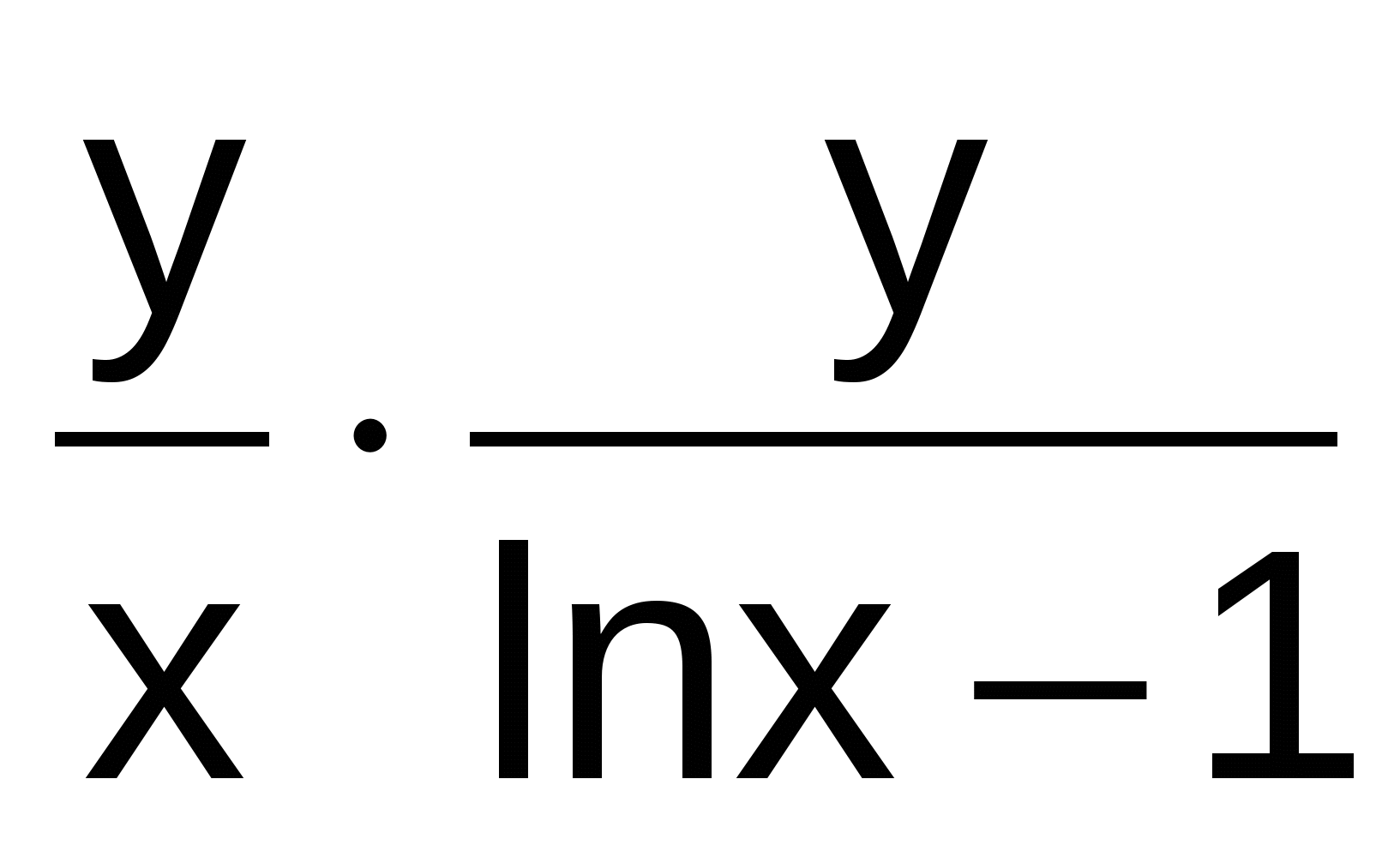
|
1
|
1,5
|
0,3
|
Y0(1) = О,5
|
|
Y' = 2x + sin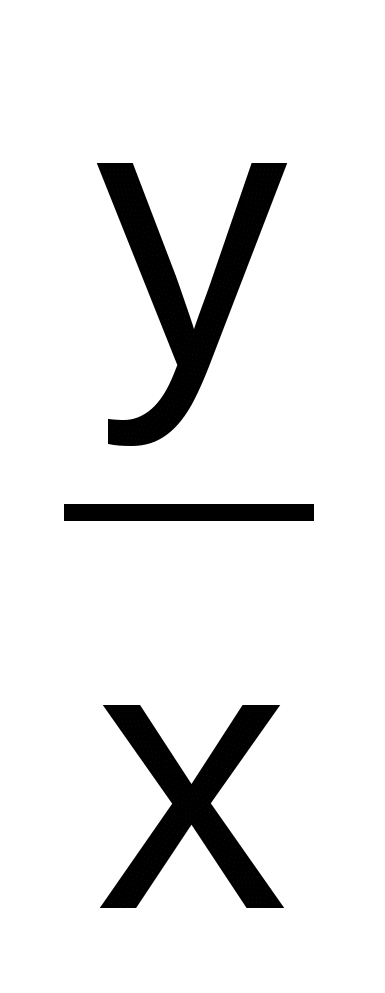
|
0,1
|
1
|
0,05
|
Y0(0,1)=1
|
|
Y' = 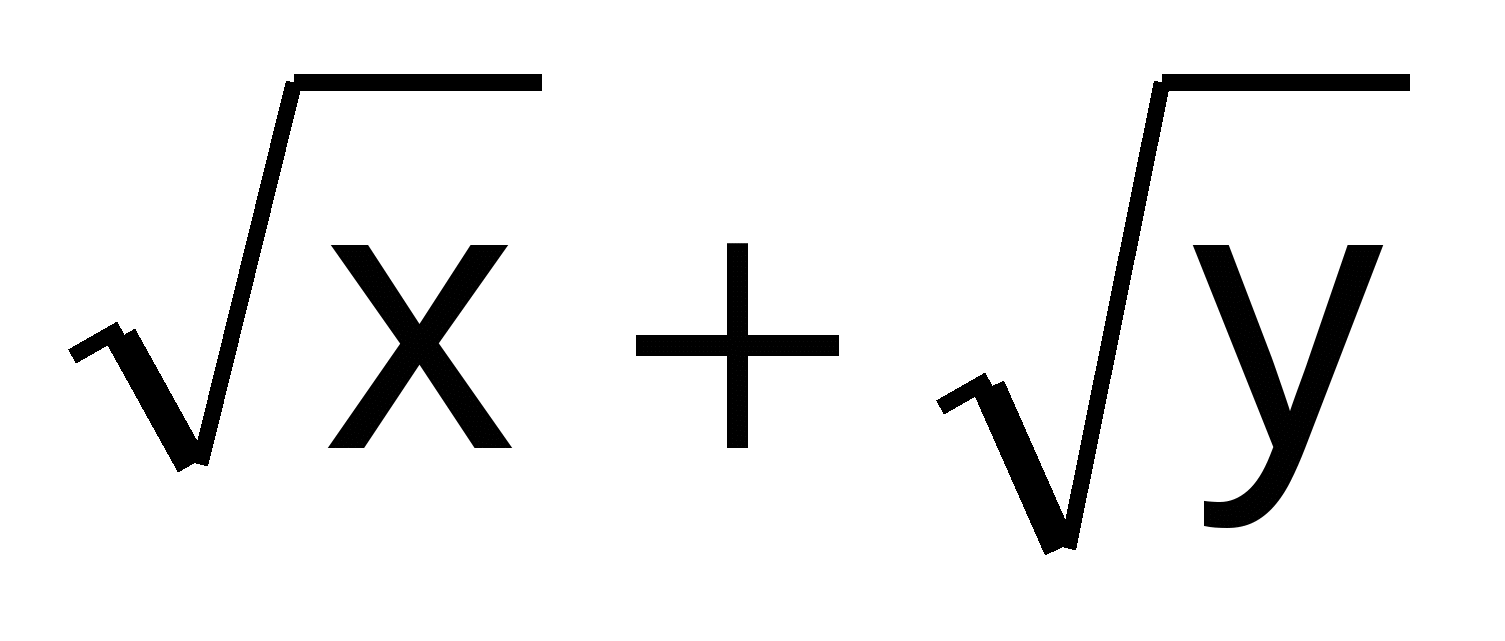
|
0
|
1
|
0,1
|
Y0(0) = 0
|
|
Y' = 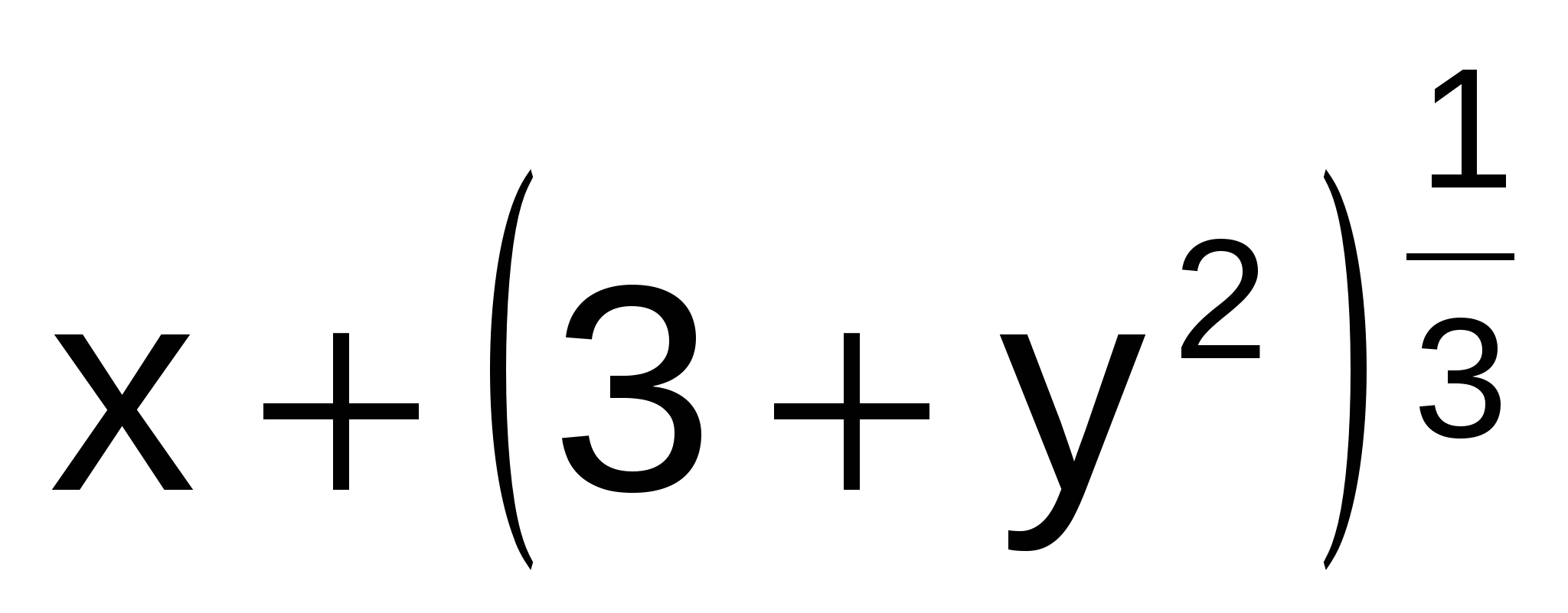
|
0
|
1
|
0,1
|
Y0(0) = 0
|
|
Y' = 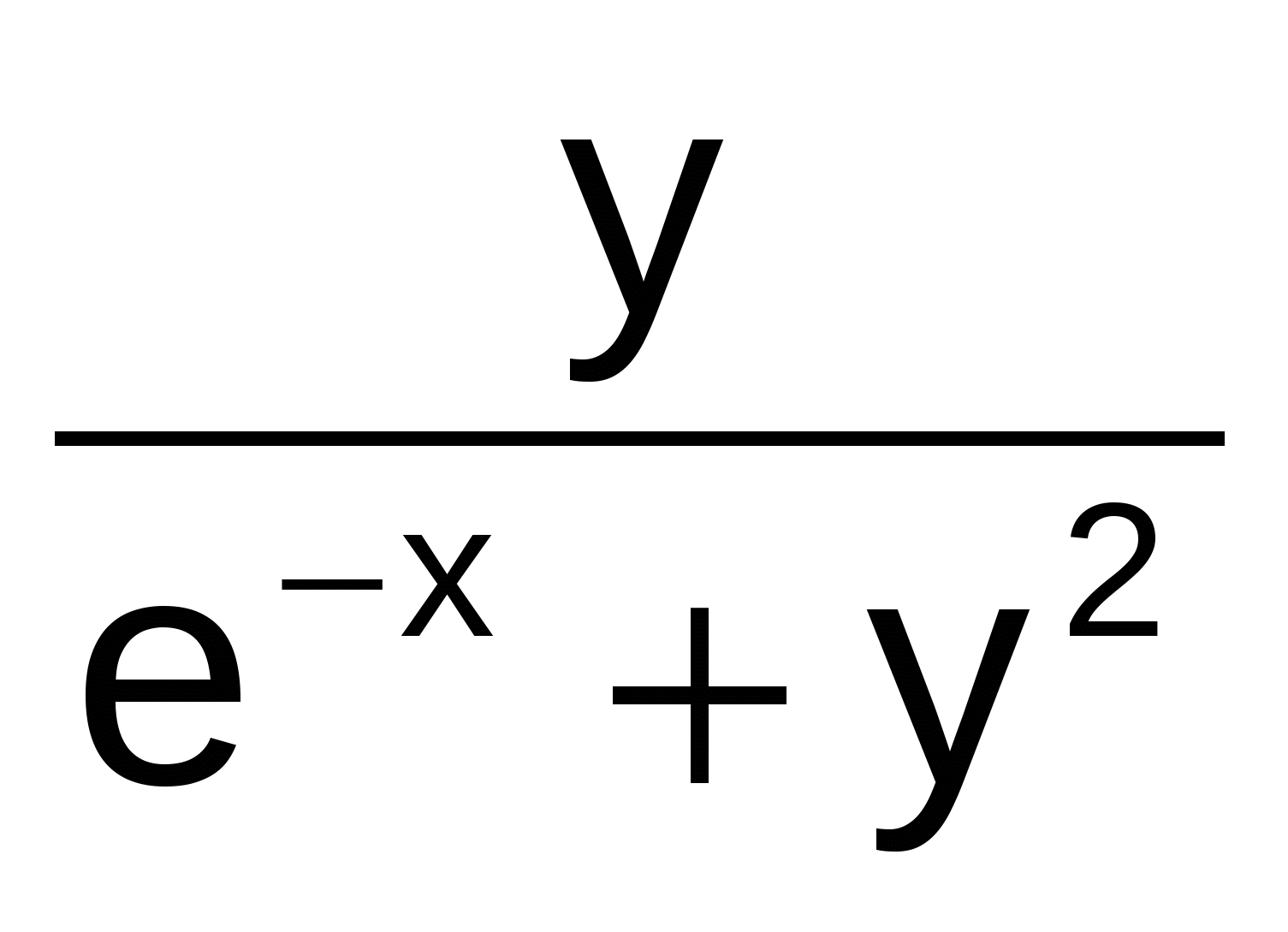
|
0,1
|
1
|
0,1
|
Y0(0,1)=1
|
|
Y' = x-y
|
0
|
1
|
0,1
|
Y0(0) = 0
|
|
Y' = 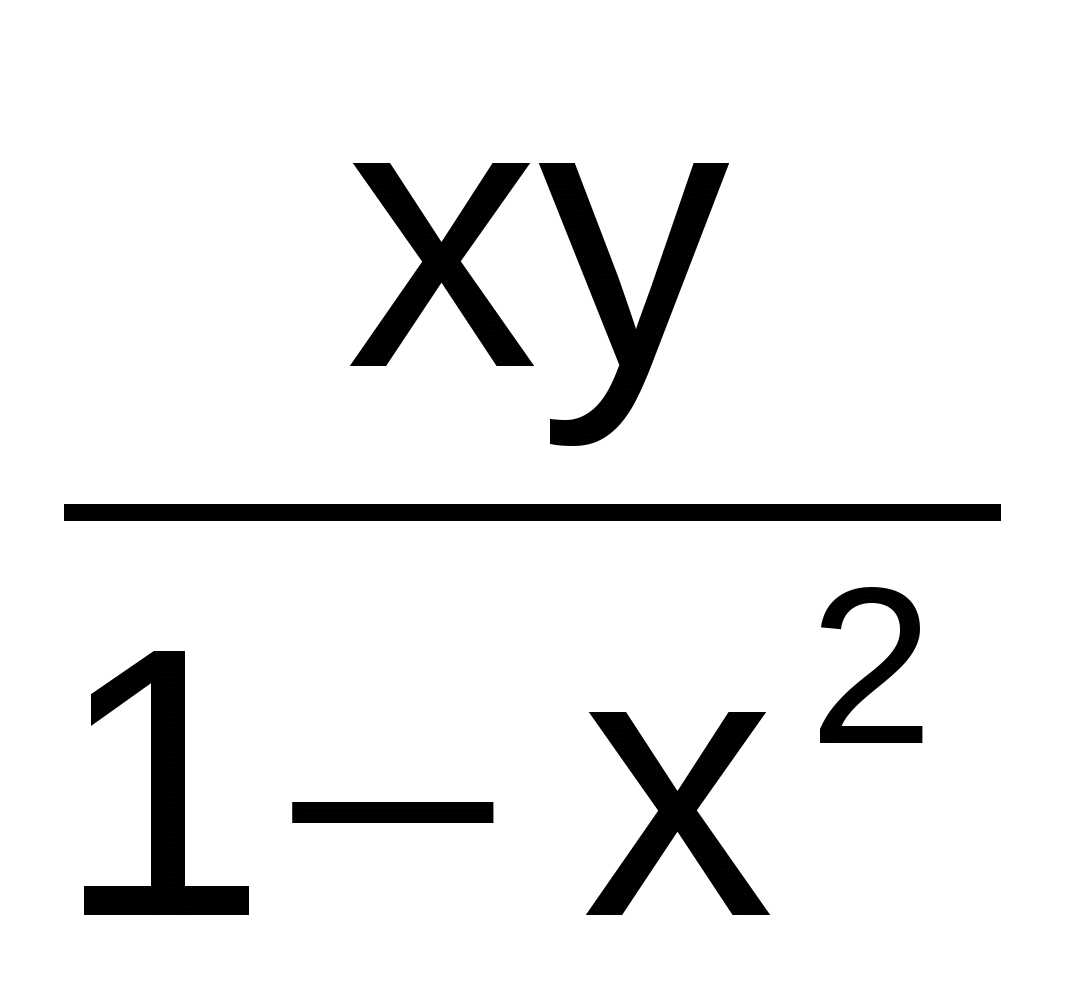
|
0
|
0,5
|
0,1
|
Y0(0,1)=1
|
|
Y' = 2xy
|
0
|
6
|
0,05
|
Y0(0) = 1
|
|
Y' = 2x – 3y
|
0
|
6
|
0,05
|
Y0(0) = 1
|
|
|
|
 Скачать 2.11 Mb.
Скачать 2.11 Mb.