Методич_стат-исправлено. Методические указания по курсу Информатика

• Название: Методические указания по курсу Информатика
• Анкор: Методич_стат-исправлено.doc
• Дата: 12.03.2019
• Размер: 2.11 Mb.
• Имя файла: Методич_стат-исправлено.doc
• Тип: Методические указания; #25584
• страница: 2 из 23

Введение

Широкое внедрение математических методов в самые разнообразные сферы деятельности сегодня уже никого не удивляет. Это не только технические и экономические науки, но и развивающиеся прикладные науки управления: менеджмент, логистика, социально-экономическое прогнозирование и т.д.

Математическое моделирование становится одним из главных направлений в технике, экономике, социологии, биологии и других областях. Поэтому специалистам различных направлений необходимо владеть концепциями и методами математического моделирования, иметь представление об инструментах, применяемых в моделировании.

При изучении курса информатики, студент знакомится с основами алгоритмизации и программирования, с пакетами прикладных программ общего назначения.

Данный лабораторный практикум по курсу «Информатики» включает следующие темы:

1. 
   статистическая обработка результатов эксперимента
   
2. 
   вычисление интегралов
   
3. 
   решение нелинейных уравнений
   
4. 
   решение дифференциальных уравнений
   
5. 
   оптимизация технологического процессов
   
6. 
   работа с файлами последовательного доступа
   
7. 
   символьные переменные.
   

ЛАБОРАТОРНАЯ РАБОТА № 1
«Статистическая обработка результатов эксперимента»

Цель работы ознакомление с основными характеристиками случайных величин.

В результате эксперимента определились такие показатели, как рост и вес человека.

рост	160 х1	170 х2	156 х3	………	………	………	……… Хn
вес	62 Y1	81 Y2	60 Y3	………	………	………	……… Yn

Обозначим х_i – рост, y_i – вес. Количество экспериментов- n, где n – размер выборки, i – текущий индекс.

Необходимо определить характеристики случайных величин (величин х и у).

Теоретические сведения

Математическая постановка задачи

(характеристики случайных величин)

1. Математическое ожидание (среднее значение)

по х:

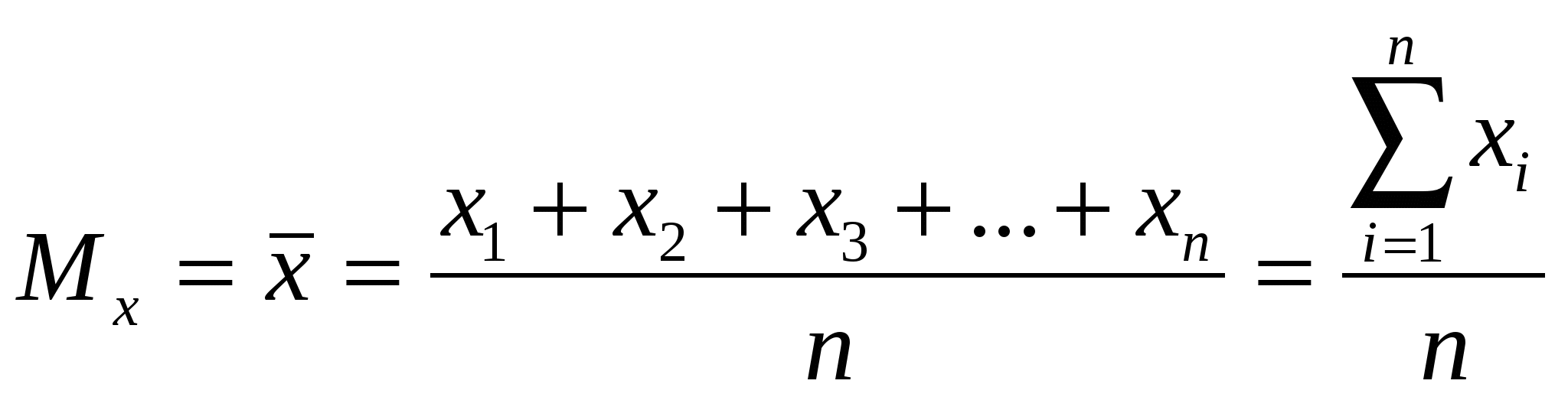
по у:

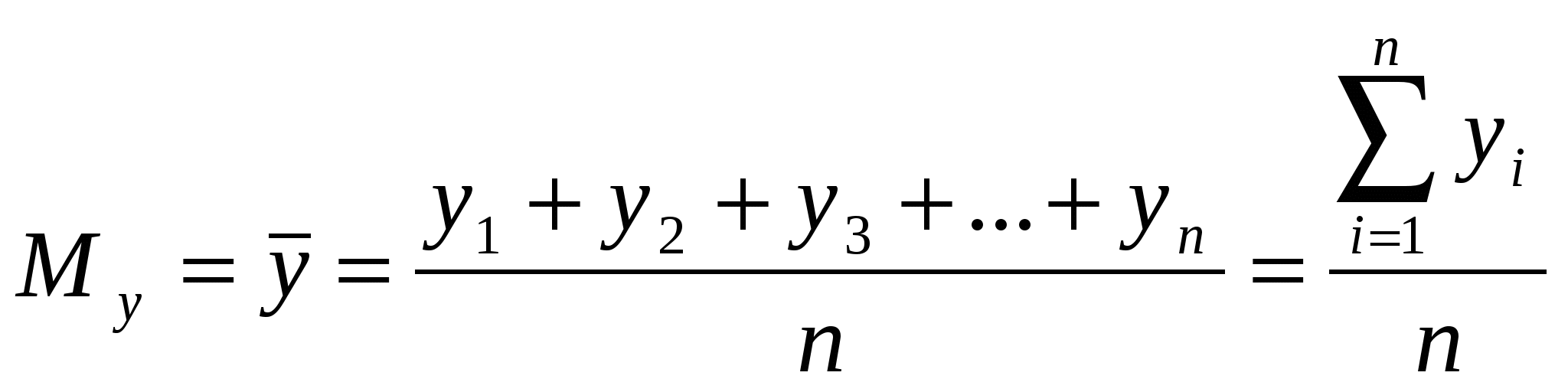
Математическое ожидание характеризует положение случайной величины на числовой оси.

2. Дисперсия

по х: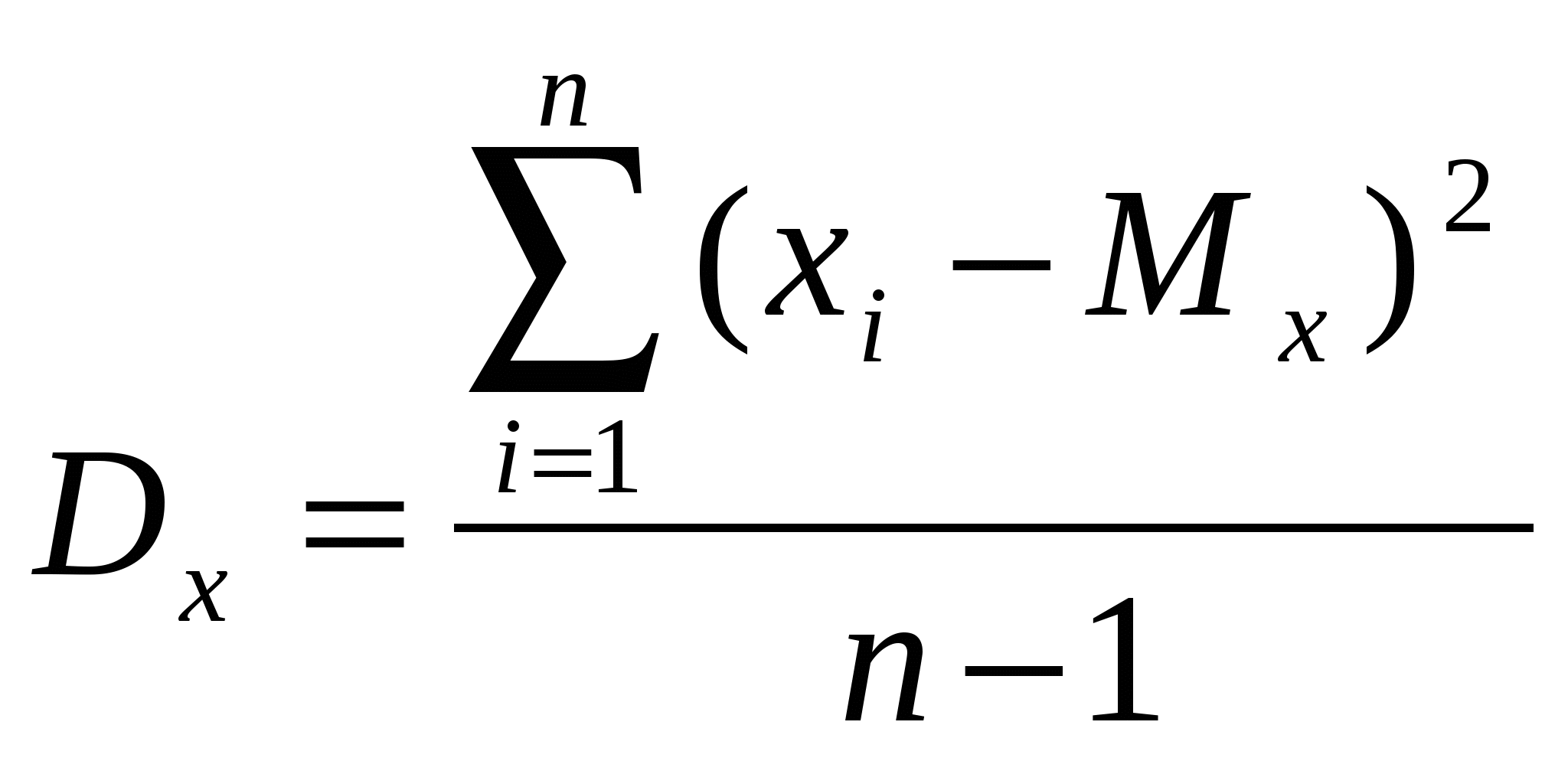

по у: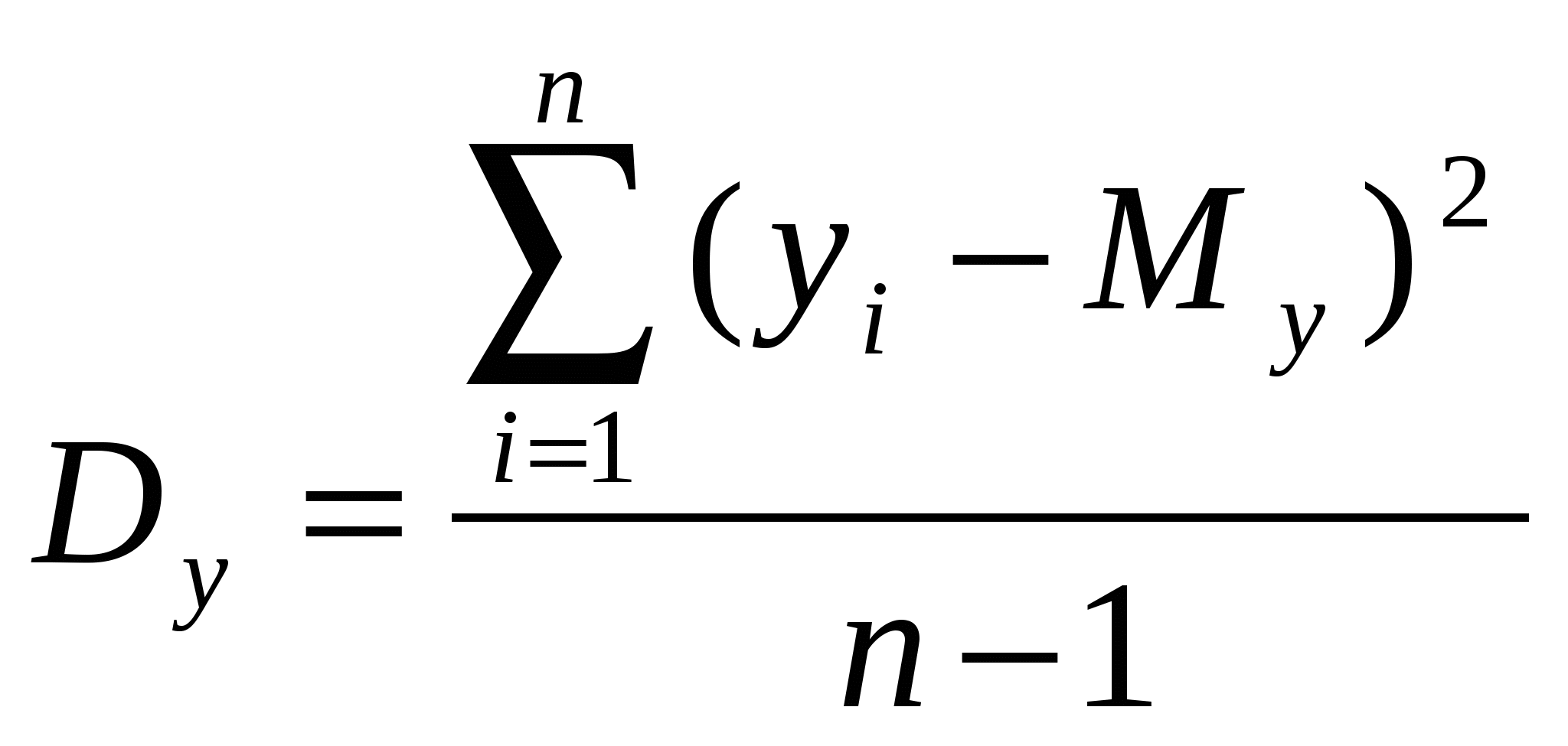

Где Mx, My – математическое ожидание.

Дисперсия характеризует разброс случайных величин. В данных формулах – разброс относительно математического ожидания.
3. Среднее квадратическое отклонение

по х:

по у:

Эта величина называется также стандартным отклонением, выражается в тех же единицах, что и величины, полученные в результате эксперимента. И зачастую оказывается более удобной характеристикой, чем дисперсия. Чем слабее варьирует признак, тем меньше среднее квадратическое отклонение.

4. 
   Коэффициент вариации
   

Коэффициент вариации необходим для сравнения изменчивости признаков, выраженных разными единицами. Дисперсия и среднее квадратическое отклонение – величины абсолютные, именованные, выражаемые в тех же единицах, что и характеризуемый ими признак.

Коэффициент вариации – относительный показатель, представляет процентное отношение среднего квадратического отклонения к математическому ожиданию

по х:

по у:

5. Нормированное отклонение

Нормированное отклонение – показатель, представленный отклонением той или иной величиной от математического ожидания, отнесённое к величине среднего квадратического отклонения:

по х:

по у:

6. Коэффициент корреляции

Коэффициент корреляции характеризует степень линейной зависимости (степень связи) между величинами х и у.

Вычисляется по формуле:



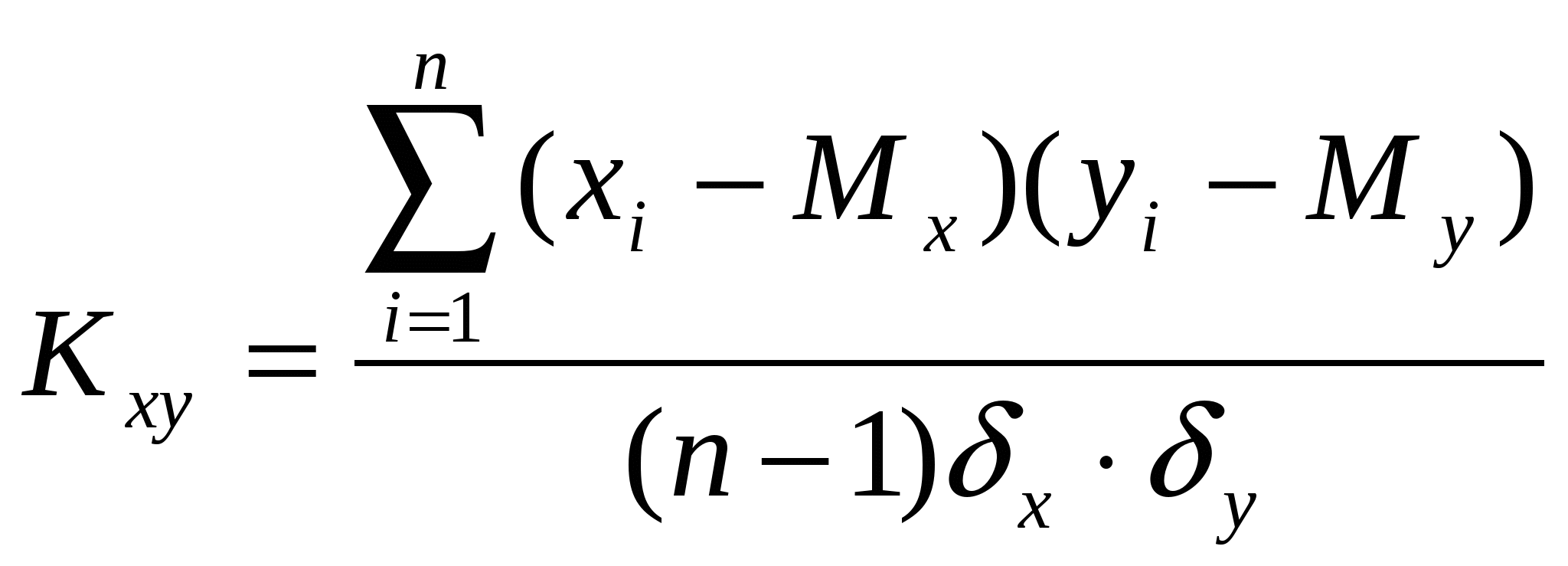
Или



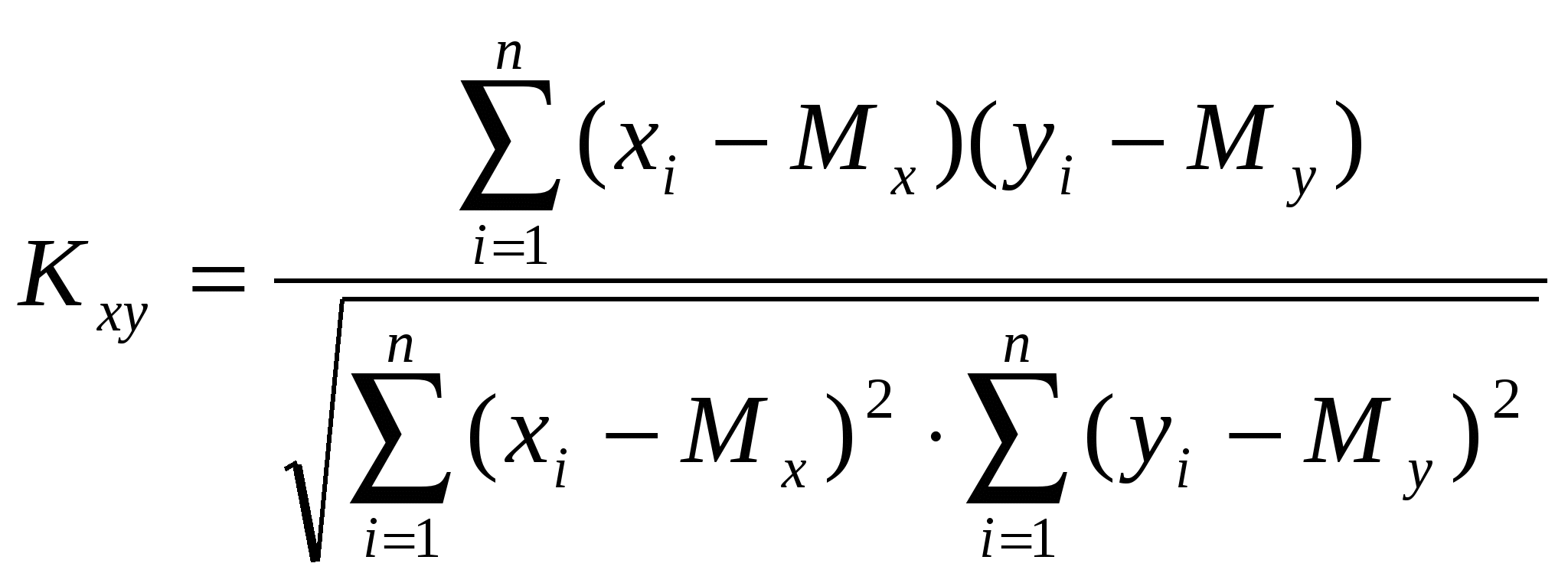
Значение К_ху изменяется в пределах от -1 до +1. Если значение К_ху > 0, то корреляция положительная (с ростом х значение у увеличивается), если К_ху < 0, то корреляция отрицательная (с ростом х значение у уменьшается).

При значении | К_ху | близком к 1 существует линейная зависимость между х и у, т.е. , знак корреляции совпадает со знаком коэффициента .