Методич_стат-исправлено. Методические указания по курсу Информатика

• Название: Методические указания по курсу Информатика
• Анкор: Методич_стат-исправлено.doc
• Дата: 12.03.2019
• Размер: 2.11 Mb.
• Имя файла: Методич_стат-исправлено.doc
• Тип: Методические указания; #25584
• страница: 5 из 23

2) Метод трапеций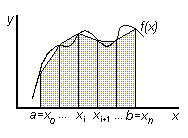

В методе трапеций график функции f(х) аппроксимируется ломаной, соединяющей точки с координатами
(x_i, у)

Рис.5

Искомое значение определенного интеграла представляется в виде суммы площадей трапеций, построенных на каждом из элементарных отрезков: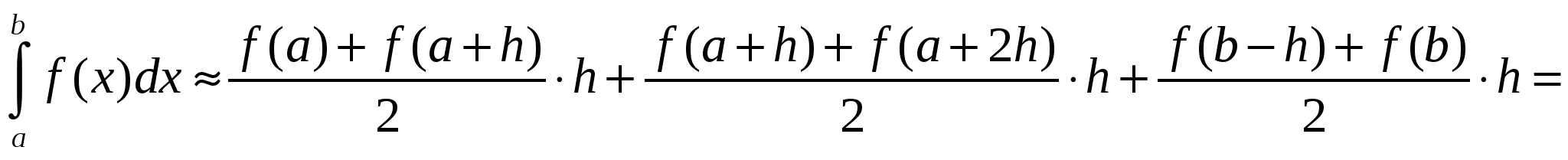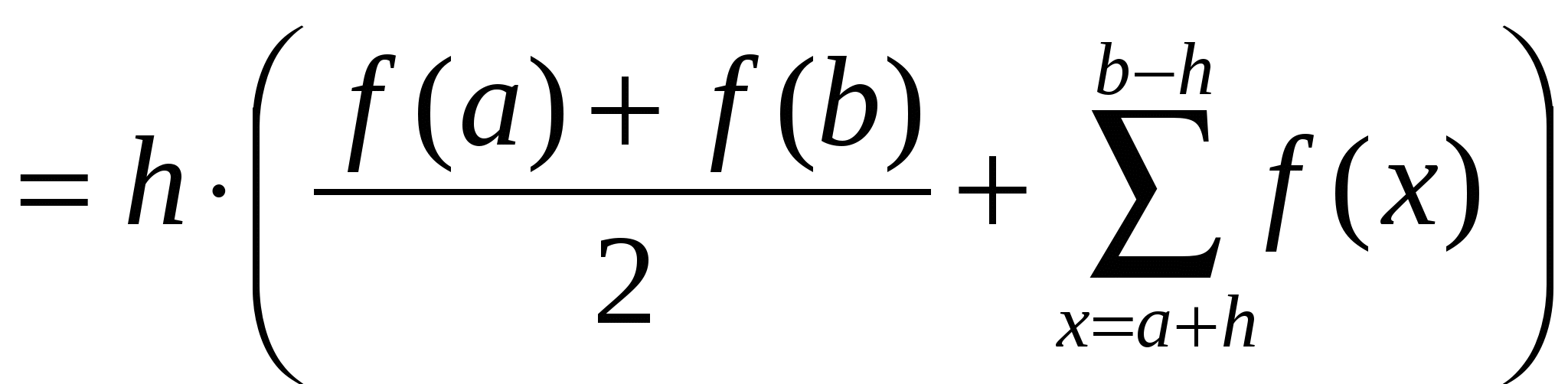

3) Метод парабол

В методе парабол (формула Симпсона) на каждом из элементарных отрезков по трем известным значениям функции f(Xj) строится парабола, заданная уравнением aх²+bх+с.

Формула для нахождения определенного интеграла может быть выведена из условия равенства значений: у_i = aх_i²+ bx_i +с:





3. Порядок выполнения работы



3.1. Получить у преподавателя вариант задания, включающий в себя подынтегральную функцию (F(Х)), отрезок интегрирования (a,b), точность вычисления значения интеграла (eps).

3.2. Исследовать подынтегральную функцию на непрерывность и существование на заданном отрезке.

3.3. Составить блок-схему для каждого метода и блок-схему головного модуля.

3.4. Написать подпрограмму для каждого метода (прямоугольников, трапеции, парабол).

3.5. Написать головной модуль.

3.6. Отладить программу и получить результаты .

3.7. Проанализировать полученные результаты и сделать выводы.

4. Содержание отчета.

4.1. Математическая постановка задачи.

4.2. Исходные данные.

4.3. Краткое описание методов. Блок-схема для каждого метода. Листинг подпрограмм.

4.4. Блок-схема головного (или управляющего) модуля. Листинг.

4.5. Распечатка полученных результатов.

4.6. Сравнительный анализ полученных результатов разными методами.

Пример выполнения работы

Вычислить интеграл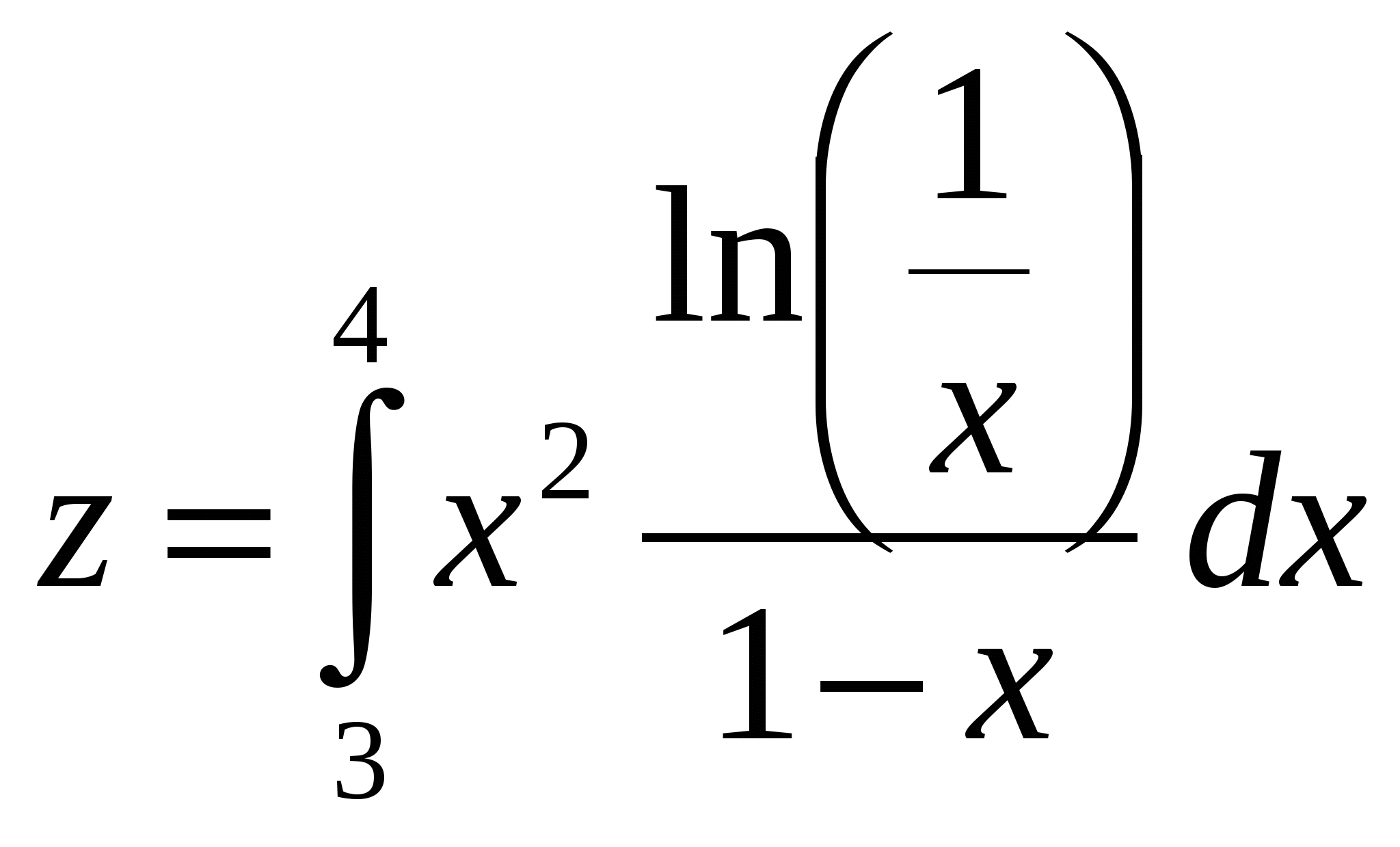

БЛОК-СХЕМА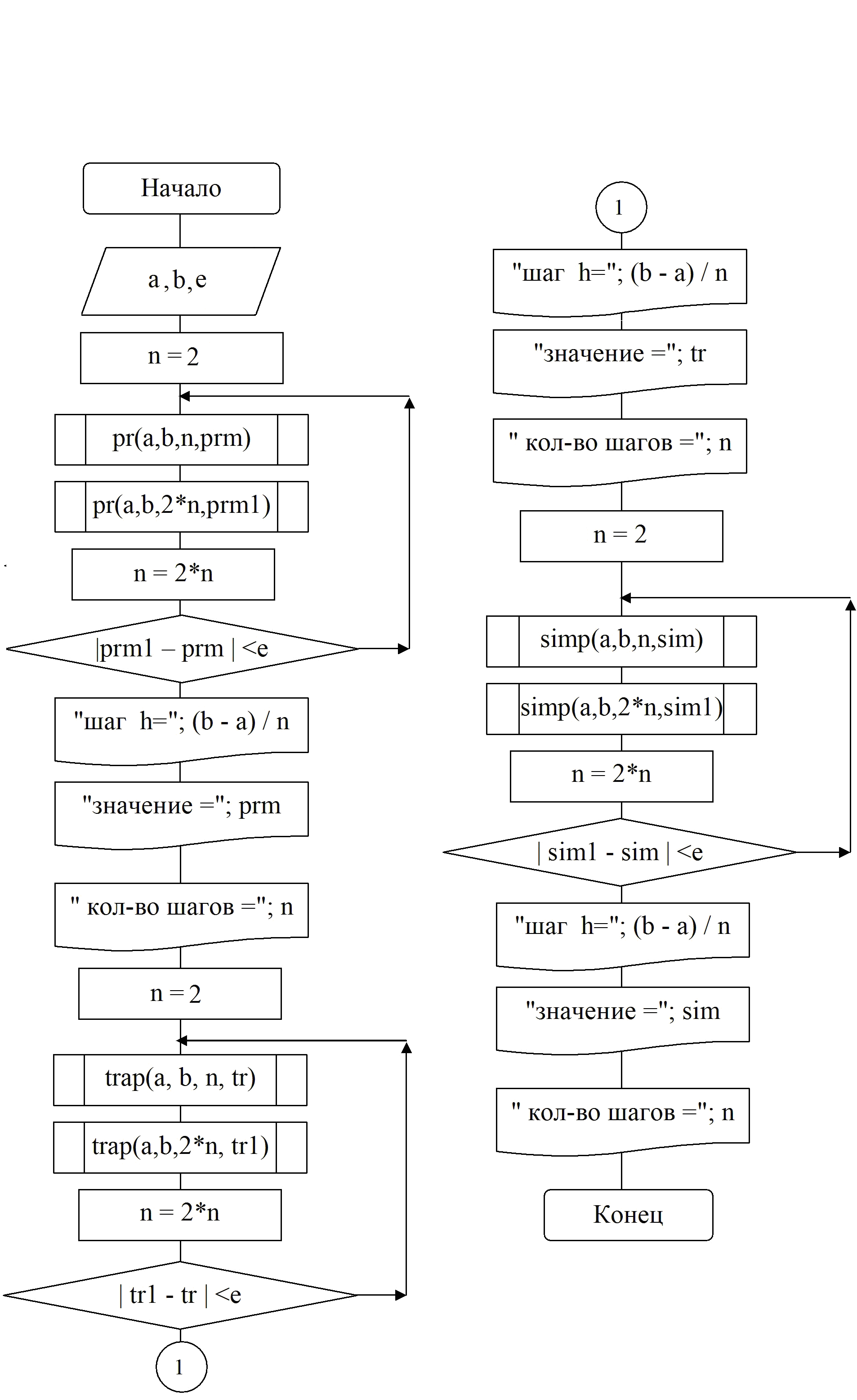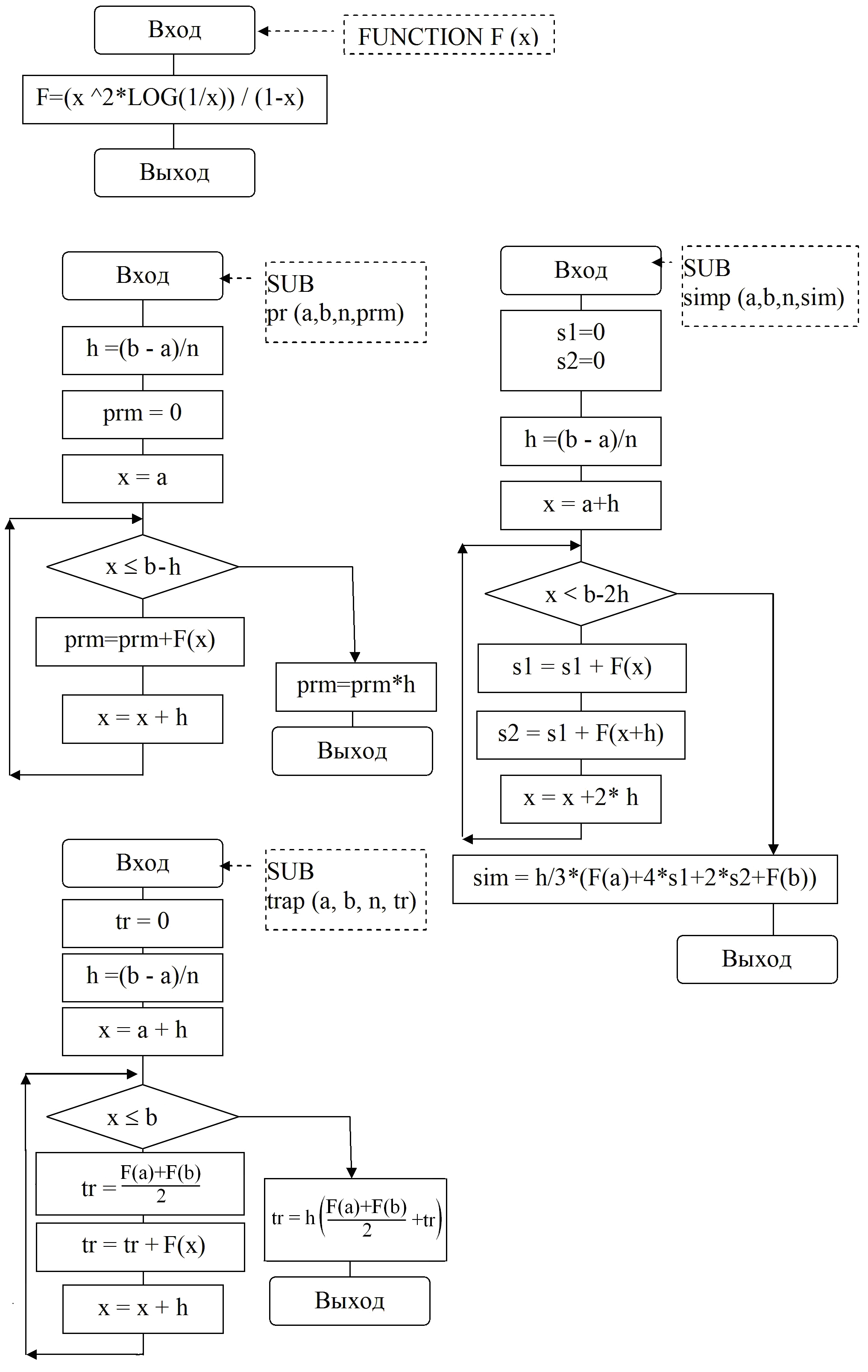

ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC

DECLARE SUB simp (a!, b!, n!, sim!)

DECLARE SUB trap (a!, b!, n!, tr!)

DECLARE SUB pr (a!, b!, n!, prm!)

DECLARE FUNCTION F! (x!)

CLS

INPUT "Введите a= "; a

INPUT "Введите b= "; b

INPUT "Введите e= "; e

n = 2

DO

CALL pr(a, b, n, prm)

CALL pr(a, b, 2 * n, prm1)

n = 2 * n

LOOP UNTIL ABS(prm1 - prm) < e

PRINT "шаг интегрирования h="; (b - a) / n

PRINT "значение интеграла по методу прямоугольника="; prm

PRINT " кол-во шагов для достижения точности Eps ="; n

PRINT

n = 2

DO

CALL trap(a, b, n, tr)

CALL trap(a, b, 2 * n, tr1)

n = 2 * n

LOOP UNTIL ABS(tr1 - tr) < e

PRINT "шаг интегрирования h="; (b - a) / n

PRINT "значение интеграла по методу трапеции="; tr

PRINT " кол-во шагов для достижения точности Eps ="; n

PRINT

n = 2

DO

CALL simp(a, b, n, sim)

CALL simp(a, b, 2 * n, sim1)

n = 2 * n

LOOP UNTIL ABS(sim1 - sim) < e

PRINT "шаг интегрирования h="; (b - a) / n

PRINT "значение интеграла по методу Симпсона="; sim

PRINT " кол-во шагов для достижения точности Eps ="; n

END
FUNCTION F (x)

F = (x ^ 2 * LOG(1 / x)) / (1 - x)

END FUNCTION
SUB pr (a, b, n, prm)

h = (b - a) / n

prm = 0

FOR x = a TO b - h STEP h

prm = prm + F(x)

NEXT x

prm = prm * h

END SUB
SUB simp (a, b, n, sim)

s1 = 0: s2 = 0

h = (b - a) / n

FOR x = a + h TO b - 2 * h STEP 2 * h

s1 = s1 + F(x)

s2 = s2 + F(x + h)

NEXT x

sim = h * (F(a) + 4 * s1 + 2 * s2 + F(b)) / 3

END SUB
SUB trap (a, b, n, tr)

tr = 0

h = (b - a) / n

FOR x = a + h TO b STEP h

tr = tr + F(x)

NEXT x

tr = h * ((F(a) + F(b)) / 2 + tr)

END SUB