Главная страница
Навигация по странице:

  • Рекомендации по решению задачи

    		•

    Методич_стат-исправлено. Методические указания по курсу Информатика


    Скачать 2.11 Mb.
    НазваниеМетодические указания по курсу Информатика
    АнкорМетодич_стат-исправлено.doc
    Дата12.03.2019
    Размер2.11 Mb.
    Формат файлаdoc
    Имя файлаМетодич_стат-исправлено.doc
    ТипМетодические указания
    #25584
    страница9 из 23
    1   ...   5   6   7   8   9   10   11   12   ...   23

    РЕЗУЛЬТАТЫ РАБОТЫ В QBASIC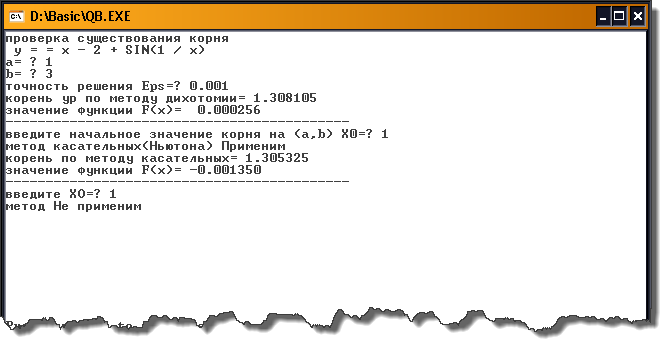



    РЕЗУЛЬТАТЫ РАБОТЫ в Eureka.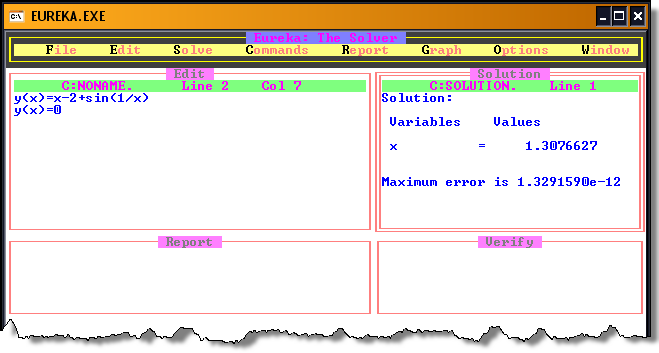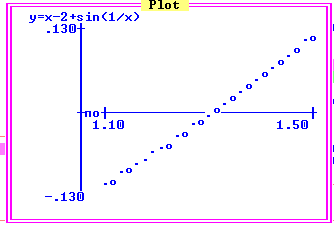




    Рекомендации по решению задачи:

    1. Решить задачу, используя ППП Eureka.

    2. Исходя из полученного решения, выбрать границы существования корня.

    3. Составить блок – схему решения и программу на QBasic.

    Контрольные вопросы
    «Уточнение корня уравнения»


    1. В чем заключается геометрический смысл метода половинного деления?

    2. Какой оператор цикла используется в процедуре дихотомии?

    3. Какими свойствами должна обладать функция F(x), чтобы методом половинного деления можно было гарантировать решение уравнения F(x)?

    4. Что необходимо для нахождения хотя ы одного действительного корня уравнения F(x) методом половинного деления?

    5. Какие процедуры функции используются в программе?

    6. Какой функцией заменяется левая часть уравнения F(x)=0 в методе итерации?

    7. Что называется сходимостью метода итерации?

    8. Каково условие сходимости метода итерации и как это условие проверяется в программе?

    9. В чем заключается геометрическая интерпретация метода Ньютона?

    10. Исходя из чего выбирается в методе Ньютона первое приближение Х0

    11. Для чего в программе предусмотрена процедура-функции для второй производной от исходной функции?

    Варианты заданий для самостоятельного решения

    Задание.


    1. Уточнить корень уравнения, используя следующие методы:

    - метод половинного деления;

    - метод простой итерации;

    - метод касательных (Ньютона).

    1. Для вариантов заданий, представленных в таблице 4, выбрать точность вычисления.

    2. Для вариантов заданий, представленных в таблице 6, вычислить корень с заданной точностью.

    3. Для вариантов заданий, представленных в таблице 7,8,9, установить границы существования корня, точность вычисления, установить границы существования корня.


    Таблица заданий № 4.

    П\П
    Вид уравнения
    Начальное приближение корня



    x – sin 2x – 1 = 0
    0



    2x ^ 3 + 4x – 1 = 0
    0.1



    x ^ 3 + 12x – 2 = 0
    0.95



    5 – x – 8lnx = 8

    4.32



    x ^ 3 + x = 1000
    9.42



    x – sin x = 0.25
    1.17



    x ^ 3 – 6x ^ 2 + 20 = 0
    2.25



    5x ^ 3 + 10x ^ 2 + 5x – 1 = 0
    0.6



    3sin+0.34x-3.8 =0
    2



    x – 3 + sin (3.6x) = 0
    0



    arcos(x)- = 0
    0



    √1- 0.4x ^ 2 – arcsin x = 0
    0



    x – 2 + sin x = 0
    1.2



    1 – x + sin x – ln (1 + x) = 0
    0



    x ^ 2 – ln (1 + x) – 3 = 0
    2



    x ^ 3 + x ^ 2 – 3 = 0
    0.6



    x ^ 3 – x – 0.2 = 0
    0.9



    5x ^ 3 – x – 1 = 0
    0.6



    x ^ 3 – 2x – 5 = 0
    1.9



    x ^ 3 + x = 1000
    9.1



    x ^ 4 + 2x ^ 3 – x – 1 = 0
    0



    x ^ 3 – x – 2 = 0
    0.9



    x – sin x/2 – 1 = 0
    0



    2 ^ 3 + 4x – 1 = 0
    0.1



    x ^ 3 + 12x – 2 = 0
    0.95


    Таблица заданий № 5

    П\П
    Вид уравнения
    Отрезок



    0.25x ^ 3 + x – 1 .2502 = 0
    0, 2



    0.1x ^ 2 – xlnx = 0
    1, 2



    3x – 4lnx – 5 = 0
    2, 4



    e ^ x – e ^ -x – 2 = 0
    0, 1



    e ^ x + lnx – 10x = 0
    3, 4



    3x – 14 + e ^ x – e ^ -x = 0
    1, 3



    3ln ^ 2x + 6lnx– 5 = 0
    1, 3



    2xsinx – cosx = 0
    0.4, 1



    xtgx – 1\3 = 0
    0.2, 1



    √ 1 – x - cos√ 1 – x = 0
    0, 1


    Таблица заданий № 6

    № вар.
    Уравнение
    Интервал
    Точность



    x – 1\ (2 + sin2x) = 0
    [0; 1]
    10 ־³



    arcsin(x\3) - √ 1 – (x\3) ^ 2 = 0
    [ 1,5; 3]
    10 ־³



    x - √ 9 –x+ x ^ 2 = 0
    [1; 2]
    10 ־³



    √1 – x ^ 2 - arcsin x = 0
    [0; 1]
    10 ־³



    tgx – (1/3)(tgx)^3 + (1/5)(tg x) ^ 5 – 1/3 = 0
    [0; 0,8]
    10 ־³



    e ^ x – e (- x) – 2 = 0
    [0; 1]
    10 ־³



    cosx – e(-(x ^ 2) / 2) + x – 1 = 0

    [0; 2]
    10 ־³



    sin(x ^ 2) + cos( x ^ 2) – 10x = 0

    [0; 1]
    10 ־³



    3sin√x + 0,35x – 3,8 = 0
    [2; 3]
    10 ־³



    √1 – 0,4 (x ^ 2) – arcsinx = 0

    [0; 1]
    10 ־³



    1/4(x ^ 3) + x – 1,25 = 0

    [0; 1]
    10 -5



    x – sin(x + 2) = 0
    [0; 1]
    10 -5



    √1 – x - cos√1 – x = 0
    [0; 1]
    10 ־³



    0,1(x ^ 2) – x lnx = 0

    [1; 2]
    10 ־³



    3x – 4 lnx – 5 = 0
    [1;4]
    10 ־³



    e ^ x + lnx – 10 x = 0

    [1; 4]
    10 ־³



    x tgx – 1/3 = 0
    [0; 1]
    10 ־³



    0,25(x ^ 3) + x – 1,25 = 0
    [0; 2]
    10 ־³



    3x – 14 + e ^ x + e (-x) = 0

    [1; 3]
    10 ־³



    2x sinx – cosx = 0
    [0,4; 1]
    10 ־³



    1/(1 + x ^ 2) – x = 0
    [1; 2]
    10 ־³



    .(tg x) ^ 2 – x = 0
    [1; 2]
    10 ־³



    x + ln(х + 0.5) - 0.5 = 0
    [0;2]
    10 ־³



    x ^3 – х - 0.2 = 0
    [1;1,1]
    10 ־³



    x^ 4 + 2х^ 3 – х – 1 = 0
    [0; 1]
    10 ־³



    x ^ 3 – 0.2х^ 2 - 0.2х - 1.2 = 0
    [1;1,5]
    10 ־³



    2sin^2х/3 – Зсоs^2х/4 = 0
    [0;П/2]
    10־³



    x ^ 4 + 0.8х ^ 3 - 0.4х ^ 2 - 1.4х - 1.2 = 0

    [-1,2;-0,5]
    10־³



    x ^ 4 - 4.1х ^ 3 + х^ 2 - 5.1х + 4.1 = 0

    [3,7;5]
    10־³



    х2 ^ х – 1 = 0
    [0;1]
    10־³


    Таблица заданий № 7

    № вар
    Уравнение
    № вар
    Уравнение



    x – sinx = 0,25 16.



    tg(0,3x + 0,4) = x ^ 2



    tg(0,58x + 0,1) = x ^ 217.



    x ^ 2 – 20sinx = 0



    √x – cos(0,387x) = 018.



    ctgx – x/4 = 0



    tg(0,4x + 0,4) = x ^ 2 19.



    tg(0,47x + 0,20 = 0



    lgx – 7/(2x + 6) = 020.



    x ^ 2 + 4sinx = 0



    tg(0,5x + 0,2) = x ^ 2 21.



    ctgx – x/2 = 0



    3x – cosx – 1 = 022.



    2x – lgx – 7 = 0



    x + lgx = 0,523.



    tg(0,44x + 0,30 = 0



    tg(0,5x + 0,1) = x ^ 2 24.



    3x – cosx – 1 = 0



    x ^ 2 + 4sinx = 025.



    ctgx – x/10 = 0



    ctg1,05x – x ^ 2 = 026.



    x ^ 2 + 4sinx = 0



    tg(0,4x + 0,3) = x ^ 2 27.



    tg(0,36x + 0,4) = 0



    xlgx – 1,2 = 028.



    x + lgx = 0,5



    1,8x ^ 2 – sin10x = 0 29.



    ctgx – x/5 = 0



    ctgx – x/4 = 030.



    2lgx – x/2 + 1 = 0



    Таблица заданий № 8

    № вар
    Уравнение
    № вар
    Уравнение



    x ^ 3 – 3x ^ 2 + 9x – 8 = 0.

    16
    x ^ 3 + 4x – 6 = 0



    x ^ 3 – 6x – 8 = 0
    17
    x ^ 3 + 0,2x ^ 2 + 0,5x + 0,8 = 0



    x ^ 3 – 3x ^ 2 + 6x + 3 = 0
    18
    x ^ 3 – 3x 62 + 12x – 12 = 0



    x ^3 – 0,1x ^ 2 + 0,4x –1,5 = 0
    19
    x ^3 -0,2 x^2 + 0,3x + 1,2 = 0



    x ^ 3 – 3x ^ 2 + 9x + 2= 0
    20
    x ^ 3 – 2x + 4 = 0



    x ^ 2 + x – 5 = 0
    21
    x ^ 3 – 0,2x ^ 2 + 0,5x – 1,4 = 0



    x ^ 3+ 0,2 x ^2 +0,5x –1,2 = 0
    22
    x ^ 3 – 3x ^ 2 + 6x – 5 = 0



    x ^ 3 + 3x + 1 = 0
    23
    x ^ 3 – 0,1x ^ 2 + 0,4x + 1,2 = 0



    x ^ 3 + 0,2x ^ 2 + 0,5x – 2 = 0
    24
    x ^ 3 – 0,2x ^ 2 + 0,5x – 1 = 0



    x ^ 3 – 3x ^ 2 + 12x – 9 = 0
    25
    x ^ 3 + 3x ^ 2 + 12x + 3 = 0



    x ^3 –0,2x ^ 2 + 0,3x – 1,2 = 0
    26
    x ^ 3 – 0,1x ^ 2 + 0,4x + 2 = 0



    x ^ 3 – 3x ^ 2 + 6x – 2 = 0
    27
    x ^ 3 – 0,2 x ^ 2 + 0,4x – 1,4 = 0



    x ^ 3 –0,1x ^ 2 +0,4x –1,5 = 0

    28
    x ^ 3 + 0,4x ^ 2 + 0,6x – 1,6 = 0



    x ^ 3 + 3x ^ 2 + 6x – 1 = 0
    29
    x ^3 + x – 3 = 0



    x ^ 3 +0,1x ^ 2+0,4x –1,2 = 0
    30
    x ^ 3 – 0,2x ^ 2 + 0,5x + 1,4 = 0


    Таблица заданий № 9

    № вар
    Уравнение
    № вар
    Уравнение



    2x ^ 3 – 3x ^ 2 – 12x – 5 = 0
    16
    2x ^ 3 – 3x ^ 2 – 12x + 1 = 0



    x ^ 3 – 3x ^ 2 – 24x – 3 = 0

    17
    x ^ 3 – 3x ^ 2 – 24x – 5 = 0



    x ^ 3 – 3x ^ 2 + 3 = 0
    18
    x ^ 3 – 4x ^ 2 + 2 = 0



    x ^ 3 – 12x + 6 = 0
    19
    x ^ 3 – 12x – 5 = 0



    x ^ 3 + 3x ^ 2 – 24x – 10 = 0

    20
    x ^ 3 + 3x ^ 2 – 24x + 1 = 0



    2x ^ 3 – 3x ^ 2 – 12x + 10 = 0
    21
    2x 6 3 – 3x^ 2 – 12x + 12 = 0



    2x ^ 3 + 9x ^ 2 – 21 = 0
    22
    2x ^ 3 + 9x ^ 2 – 6 = 0



    x ^ 3 – 3x ^ 2 + 2,5 = 0
    23
    x ^ 3 – 3x ^ 2 + 1,5 = 0



    x ^ 3 + 3x ^ 2 – 2 = 0
    24
    x ^ 3 – 3x ^ 2 – 24x + 10 = 0



    x ^ 3 + 3x ^ 2 – 3,5 = 0
    25
    x ^ 3 + 3x ^ 2 – 24x – 3 = 0



    x ^ 3 + 3x ^ 2 – 24x + 10 = 0

    26
    x ^ 3 – 12x – 10 = 0



    x ^ 3 – 3x ^ 2 – 24x – 8 = 0

    27
    2x ^ 3 + 9x ^ 2 – 4 = 0



    2x ^ 3 + 9x ^ 2 – 10 = 0
    28
    2x ^ 3 – 3x ^ 2 – 12x + 8 = 0



    x^ 3 – 12x + 10 = 0
    29
    X ^ 3 + 3x ^ 2 – 1 = 0



    x ^ 3 +3x ^ 2 – 3 = 0

    30
    x ^ 3 – 3x ^ 2 + 3,5 = 0



    1   ...   5   6   7   8   9   10   11   12   ...   23

    написать администратору сайта