|
|
Методич_стат-исправлено. Методические указания по курсу Информатика
Контрольные вопросы
Какие переменные называют символьными?
Где используются переменные текстового типа?
Что могут содержать текстовые переменные?
В чем состоит формат ASCII ?
Какие типы строковых переменных Вы знаете?
Какими способами может быть осуществлении присвоение значения текстовой переменной?
Какой знак используется для сложения текстовых переменных?
С помощью, каких знаков производится сравнение текстовых переменных?
В каком случае текстовые переменные считаются равными?
Какой принцип используется при сортировке переменных?
Перечислите функции работы с символьными переменными?
Что выполняет оператор MID$ ?
Что выполняет функция LEN?
Что выполняют функции LEFT$ и RIGHT$ ?
Что выполняет функция INSTR$ ?
Для чего предназначается функция MID$ ?
Что называют логической группой?
В чем заключается анализ символа?
На чем основаны алгоритмы выделения слов?
Как осуществляется перестановка элементов текста?
Введите строку А$ и определить, сколько в ней 1) букв русского алфавита; 2) заглавных латинских букв; 3) цифр.
Введите строки А$ и В$. Определите, сколько раз В$ входит в A$.
Введите строки А$ и В$. Удалите из А$ все вхождения В$.
Упорядочить по алфавиту вектор A$( 10), состоящий из десяти любых.
1). латинских букв; 2). русских букв; 3). цифр.
Упорядочьте в обратном алфавитном порядке вектор A$(10). Каждый элемент анализировать по всем знакам.
Введите переменную А$. Замените вес сочетания С$ на B$.
Введите текст А$. Считая словом непрерывную последовательность букв, выделите все слова A$ в отдельный массив.
Введите текст А$. Удалите все слова, которые встречаются больше двух раз, оставив только первое вхождение каждого такого слова.
Введите название переменной как текстовую строку. Проверьте, соответствует ли ее название требованиям QBasic.
Дана строка, содержащая английский текст. Найти количество слов, начинающихся с буквы В.
.Дана строка. Подсчитать, сколько в ней букв g, k, t.
Дана строка, содержащая текст. Найти длину самого короткою слова и самого длинного слова.
Дана строка, содержащая текст, закапчивающийся точкой. Вывести на экран слова, содержащие три буквы.
Дана строка. Подсчитать самую длинную последовательность подряд идущих букв а.
Дана строка. Указать тс слова, которые содержат хотя бы одну букву к.
В строке между словами вставить вместо пробела запятую и пробел.
Определить, сколько раз в строке встречается заданное слово.
18. Дана строка. Преобразовать ее, заменив точками все двоеточия (:),
Строка содержит произвольный русский текст. Проверить, каких букв в нем больше: гласных или согласных.
Результаты вступительных экзаменов представлены в виде списка из Nстрок, в каждой строке которого записаны фамилия студента и отметки по каждому из М экзаменов. Определить количество абитуриентов, сдавших вступительные экзамены только на «отлично».
Для заданного текста определить длину содержащейся в нем максимальной серии символов, отличных от букв.
Отредактировать заданное предложение, удаляя из него все слова с нечетными номерами.
ЛАБОРАТОРНАЯ РАБОТА № 6
Оптимизация технологического процесса. Методы оптимизации функции 1-ой переменной Цель работы
Ознакомление с методами одномерной оптимизации (поиска максимума и минимума).
Оптимизация функций одной переменной
Постановка задачи
На практике часто возникает задача нахождения экстремума некоторой целевой функции F(x). Такая функция одного параметра x описывает некоторую кривую на плоскости.
На определённом интервале функция может иметь одно (рис. 1а) или несколько экстремальных значений (рис. 1б).
Функция, изображённая на рис. 1а называется унимодальной.
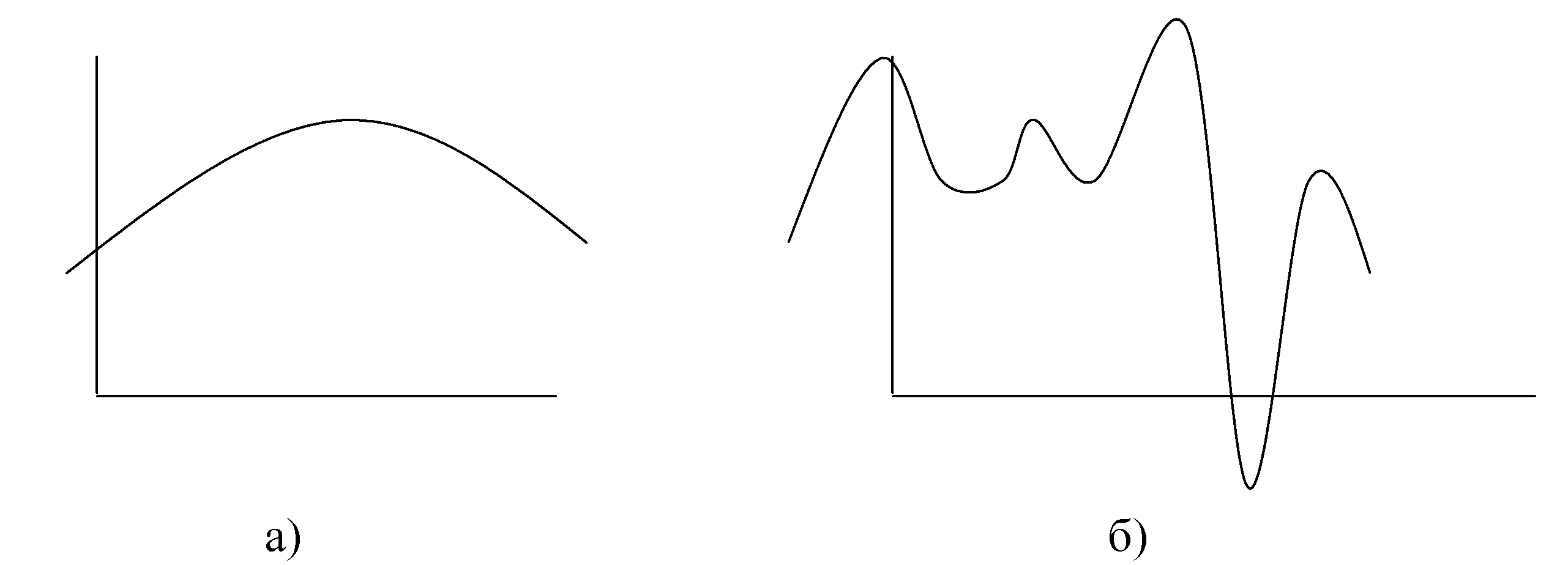
Рис. 1. Функции одного параметра x описывающие некоторую кривую на плоскости.
Функция на рис. 1б имеет несколько экстремумов (максимумов или минимумов). Из них главный (оптимальное решение для рассматриваемого интервала) называется глобальным.
Унимодальная функция не обязательно должна быть гладкой (рис. 2 а), она может быть ломаной (рис. 2б), разрывной (рис. 2в).
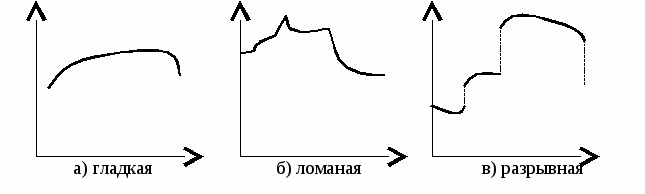 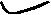
Рис. 2. Унимодальные функции
Рассматриваемые методы справедливы для функций на рисунке 2а, а для функций на рисунках 2б, 2в могут использоваться на отдельных интервалах.
Если целевая функция унимодальная, то можно сузить интервал исследования функции на оптимум путём определения значений целевой функции в двух точках интервала задания функций F(x1) и F(x2) и последующего поинтервального сравнения. При этом возможны три случая (рис. 3):
1) если F(x1) > F(x2),то xопт < x2, т.е. оптимум не может находиться правее, интервал [x2 , x] из дальнейшего рассмотрения исключается
2) если F(x1) < F(x2), то хопт > x1
3) если F(x1) = F(x2), то x1 < хопт < x2
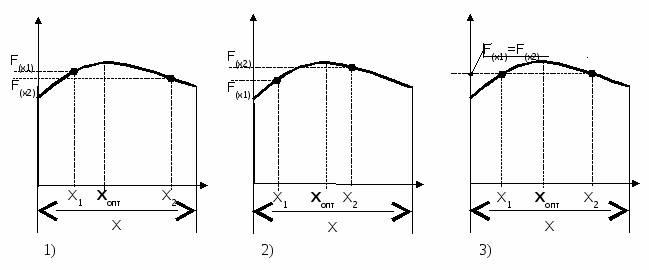
Рис. 3. Определение значений целевой функции в двух точках интервала задания функций
Последовательно сужая интервал исследования, в котором находится оптимальное значение функции, можно с достаточной степенью точности найти оптимальное значение переменной.
Задача поиска экстремумов сводится к их локализации и уточнению значений x и F(x) в точке экстремума. В дальнейшем для функций одной переменной под экстремумом будем подразумевать максимум F(x).
Поскольку максимуму функции F(x) соответствует минимум функции - F(x), то, сменив знак у F(x), программами поиска максимума можно пользоваться и для поиска минимума функций. Будем также полагать, что на изменения x (если это особо не оговорено) накладываются ограничения в виде неравенств a < x < b, где a и b – границы интервала поиска. В пределах отрезка [a , b] функцию считаем унимодальной, т.е. содержащей один максимум.
С помощью численных методов мы непосредственно находим максимум (минимум) функции F(x) в некотором интервале, в котором, как предполагается, лежит максимум (минимум). Иногда это единственно возможная стратегия поиска.
На пример, стоимость проведения химического процесса может зависеть от температуры процесса. Инженер знает, что стоимость является функцией от T, хотя может и не знать явного вида функции. Однако он может поставить эксперимент и провести эксперимент при различных температурах и, следовательно, найти стоимость для этих температур и определить минимальную стоимость и температуру проведения процесса, при которой она достигается.
Алгоритм нахождения максимума функции
Простейшая задача нахождения максимума функции решается по следующему алгоритму:
Задаются границы a и b, в пределах которых имеется максимум функции.
Интервал [a,b] разбивается на определенное количество шагов.
Функция табулируется в пределах заданного интервала, и каждое вычисленное значение функции сравнивается с максимальным (заданным до начала табулирования).
Находится максимальное значение функции на заданном интервале с определенным шагом и выводится на печать.
БЛОК-СХЕМА АЛГОРИТМА ИМЕЕТ ВИД:
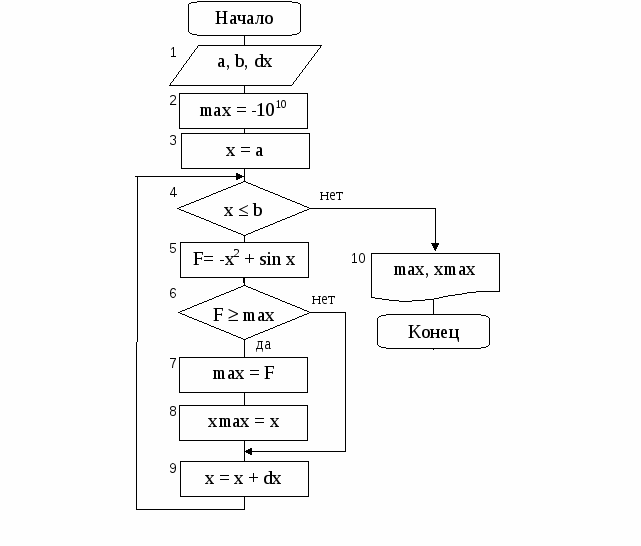
Рис. 4. Блок – схема алгоритма нахождения максимума функции
Естественно, что с уменьшением шага изменения аргумента точность вычисления максимума увеличивается.
Можно воспользоваться и следующим алгоритмом:
Найти значение максимума по алгоритму, представленному выше.
Для дальнейшего рассмотрения выбрать отрезок [xmax-dx, xmax+dx] и выполнить вычисление максимума с шагом, например, dx/10.
Сравнить два найденных значения.
max1 – значение максимума с шагом dx и max2 – значение максимума с шагом dx/10. Если |max2-max1| <=E (где Е – заданная степень точности вычисления), то закончить решение задачи и max2 вывести на печать, если нет, то вычисление продолжить дальше, повторяя п.2.
Такую задачу удобнее решать, используя процедуру нахождения максимального значения функции.
Блок – схема решения задачи имеет вид:
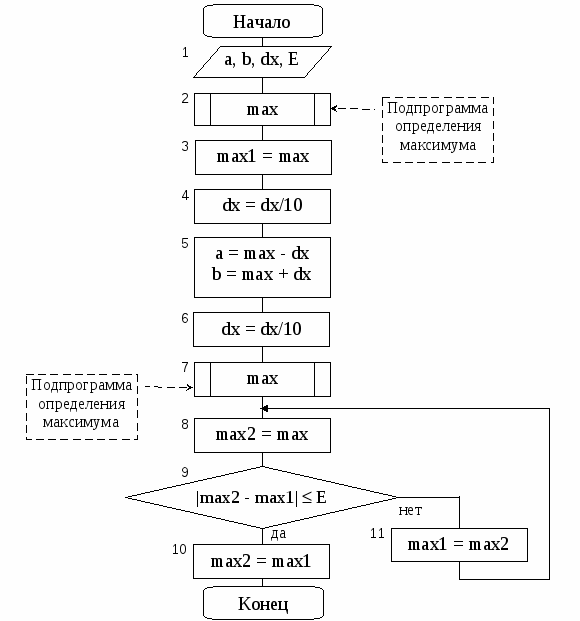
Рис. 5. Блок – схема алгоритма нахождения максимума функции
|
|
|
 Скачать 2.11 Mb.
Скачать 2.11 Mb.