Методич_стат-исправлено. Методические указания по курсу Информатика

• Название: Методические указания по курсу Информатика
• Анкор: Методич_стат-исправлено.doc
• Дата: 12.03.2019
• Размер: 2.11 Mb.
• Имя файла: Методич_стат-исправлено.doc
• Тип: Методические указания; #25584
• страница: 12 из 23

БЛОК-СХЕМА АЛГОРИТМА РЕШЕНИЯ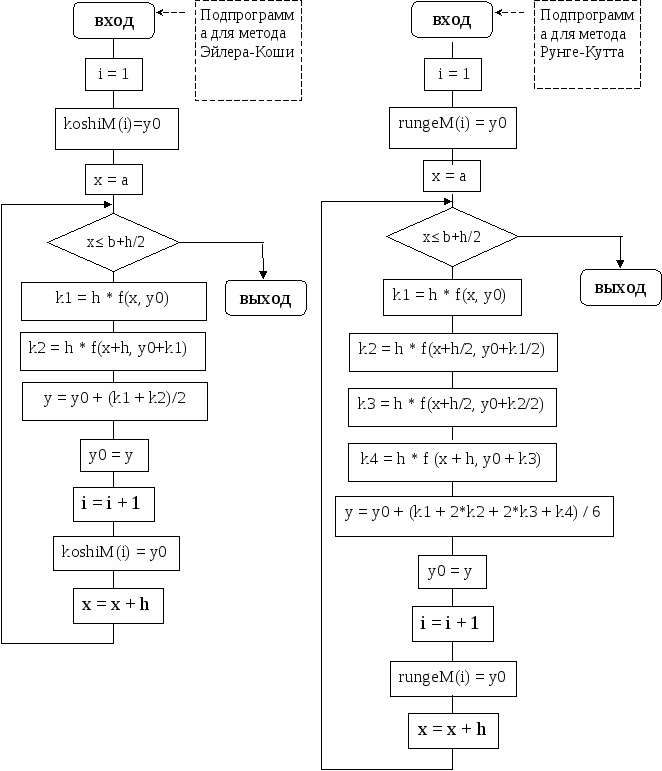

Запись всех подпрограмм можно осуществить через меню оболочки QBasic:

1. 
   Alt - вход в меню
   
2. 
   EditNew SUB … - создание новой подпрограммы
   
3. 
   EditNew FUNCTION… - создание новой подпрограммы функции
   
4. 
   Набираем в диалоговом окне новое имя подпрограммы (например: eiler)
   

На экране появляется заготовка для создания подпрограммы:

SUB <имя подпрограммы, параметры>

<текст подпрограммы>

END SUB

1. 
   Приступаем к написанию подпрограммы между ключевыми словами SUB и END SUB
   
2. 
   Все вспомогательные подпрограммы объединяются управляющей программой или головным модулем.
   
3. 
   Переход от текста управляющей программы к текстам подпрограммам происходит при нажатии клавиш F2.
   

ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC

Головной модуль на языке QBasic

DECLARE SUB eiler (a!, b!, h!, y0!)

DECLARE SUB koshi (a!, b!, h!, y0!)

DECLARE SUB runge (a!, b!, h!, y0!)

DECLARE FUNCTION f! (x!, y0!)

CLS

DIM SHARED eilerM(1000), koshiM(1000), rungeM(1000)

INPUT "левый конец интервала a= "; a

INPUT "правый конец интервала b= "; b

INPUT "шаг "; h

INPUT "краевое значение функции Y0= "; y0

yy = y0 'сохранение краевого значения функции

REM Вызов Метода Эйлера

CALL eiler(a, b, h, yy)

yy = y0
REM Вызов Метода Эйлера-Коши

CALL koshi(a, b, h, yy)

yy = y0

REM Вызов Метода Рунге-Кутта

CALL runge(a, b, h, yy)

PRINT "--------------------------------------------------------------"

PRINT "│ x │ elier │ koshi │ runge │"

PRINT "--------------------------------------------------------------"

L$ = "│ #.# │ ##.##### │ ##.##### │ ##.##### │"

i = 1

FOR x = a TO b + h / 2 STEP h

PRINT USING L$; x; eilerM(i); koshiM(i); rungeM(i)

i = i + 1

NEXT x

PRINT "--------------------------------------------------------------"

END

Первые четыре строчки пишутся автоматически при присоединении подпрограмм к головному модулю в результате выполнения команды Save All.

Подпрограмма для решения дифференциального уравнения
методом Эйлера:

SUB eiler (a, b, h, y0)

i = 1

eilerM(i) = y0

FOR x = a TO b + h / 2 STEP h

y = y0 + h * f(x, y0)

y0 = y

i = i + 1

eilerM(i) = y0

NEXT x

END SUB

Подпрограмма для решения дифференциального уравнения
методом Эйлера-Коши:

SUB koshi (a, b, h, y0)

i = 1

koshiM(i) = y0

FOR x = a TO b + h / 2 STEP h

k1 = h * f(x, y0)

k2 = h * f(x + h, y0 + k1)

y = y0 + (k1 + k2) / 2

y0 = y

i = i + 1

koshiM(i) = y0

NEXT x

END SUB

Подпрограмма для решения дифференциального уравнения
методом Рунге-Кутта:

SUB runge (a, b, h, y0)

i = 1

rungeM(i) = y0

FOR x = a TO b + h / 2 STEP h

k1 = h * f(x, y0)

k2 = h * f(x + h / 2, y0 + k1 / 2)

k3 = h * f(x + h / 2, y0 + k2 / 2)

k4 = h * f(x + h, y0 + k3)

y = y0 + (k1 + 2 * k2 + 2 * k3 + k4) / 6

y0 = y

i = i + 1

rungeM(i) = y0

NEXT x

END SUB
Процедура функция:

FUNCTION f (x, y0)

f = < функция соответствующего варианта >

END FUNCTION

Построение в Excel графика решений

1. 
   Для построения графика в Excel следует:
   
2. 
   Набить таблицу значений из Qbasic (в каждом столбце результат решения дифференциального уравнения соответствующим методом).
   

X	Метод Эйлера	Метод Эйлера-Коши	Метод Рунге-Кутта
0,5	0,672484	0,678814	0,678894
0,6	0,757629	0,770744	0,770909
0,7	0,855875	0,876242	0,876498
0,8	0,967663	0,995754	0,996108
0,9	1,093427	1,129714	1,130172
1	1,233588	1,278529	1,279097
1,1	1,388542	1,44257	1,443255
1,2	1,558648	1,622153	1,62296
1,3	1,74421	1,817519	1,818455
1,4	1,945463	2,028813	2,029882
1,5	2,162545	2,256061	2,257268

1. 
   Выделить столбцы три столбца – Метод Эйлера, метод Эйлера-Коши, метод Рунге-Кутта.
   
2. 
   Дальше в меню выбрать: Вставка  Диаграмма.
   
3. 
   Появиться меню «Мастера диаграмм».
   
4. 
   Выбрать: на вкладке «Стандартные»  График  График с маркерами, помечающими точки данных  Далее.
   
5. 
   Откроется окно «Исходные данные».
   
6. 
   В окне «Исходные данные», выбрать вкладку Ряд  Подписи оси Х, нажать маркер . Рисунок 1.
   

Рисунок 1.

1. 
   Выделить столбец Х, только цифры. Нажать Далее.
   
2. 
   Легенду разместить в низу. Нажать Далее  Готово (рис.1)
   
3. 
   Добавить Линию тренда, уравнение и R². (рис.2)
   

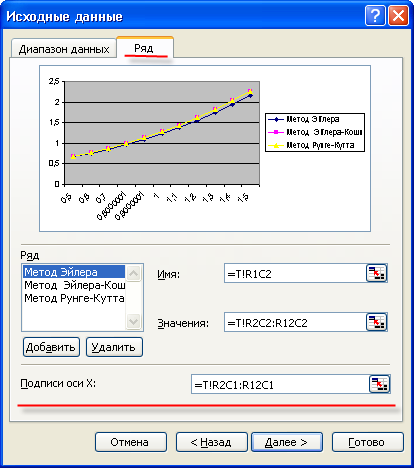
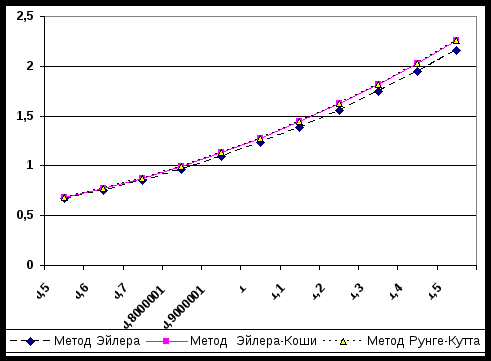Рисунок 1

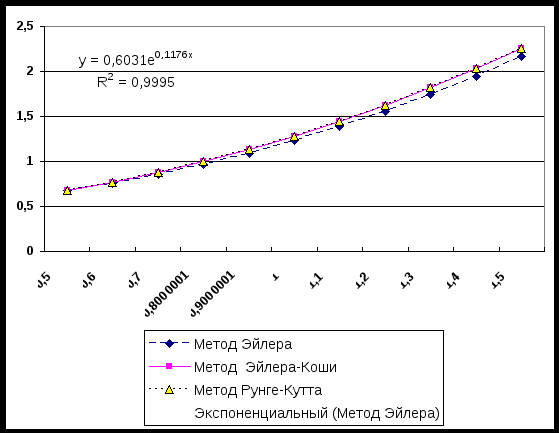Рисунок 2