Методич_стат-исправлено. Методические указания по курсу Информатика
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
3. Порядок выполнения работы1. Получить у преподавателя вариант задания, включающий в себя трансцендентное или алгебраическое уравнение ( F(x) = 0), отрезок для поиска решения ( a, b), точность вычисления значения корня (eps) и задание, каким из методов (все методы) решить задачу. 2. Исследовать существование корня на заданном отрезке, требования к функции: разные знаки на концах отрезка, непрерывность). 3. Выяснить, с какой стороны отрезка строить приближение к решению уравнения: если знак второй производной совпадает со знаком функции (f(х)- f"(х) > 0), то приближение строим елевой стороны отрезка, в противном случае - с левой стороны. 4. Написать подпрограмму для вычисления функции F(х). 5. Написать подпрограмму, например для первого метода дихотомии. 6. Написать подпрограмму, например, для второго метода касательных или простой итерации. 7. Найти первую производную функции F(x) и оформить её вычисление процедурой функции (для метода касательных). 8. Найти приведённую функцию и оформить её вычисление процедурой функции. 9. Написать головной модуль. 10. Отладить программу и получить результат. Пример выполнения лабораторной работы.
Решить уравнение методом дихотомии, простой итерации, методом касательных. a=1 b=3 F(x) = x - 2 + SIN(1 / x) - исходная функция G (x) = 2 - SIN(1 / x) - приведенная функция F1 (x) = 1+cos(1/x) 1-ая ПРОИЗВОДНАЯ ОТ F F2 (x) = -sin(1/x) 2-ая ПРОИЗВОДНАЯ ОТ F G1(x)=-cos(1/x) 1-ая ПРОИЗВОДНАЯ ОТ G e = 0.001 БЛОК-СХЕМА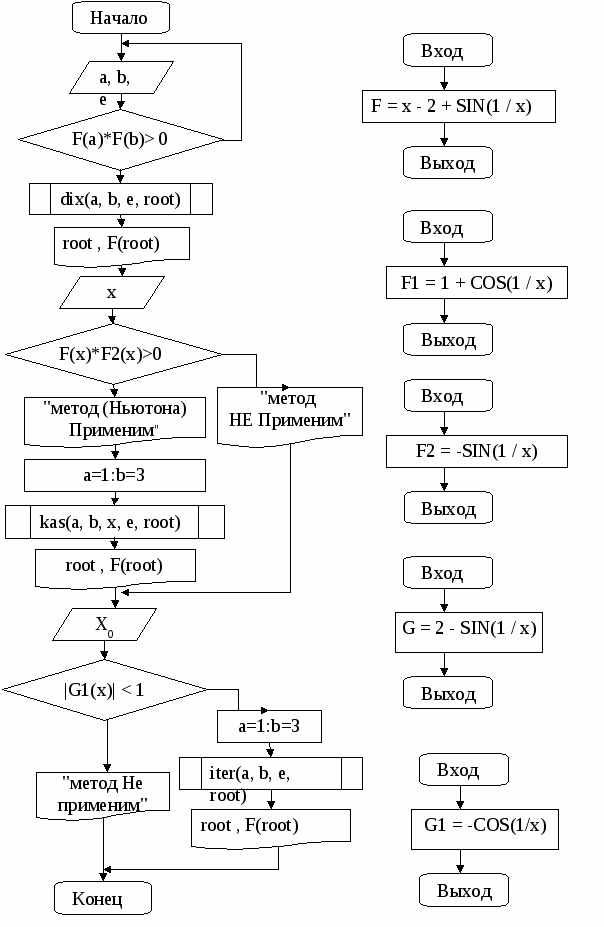  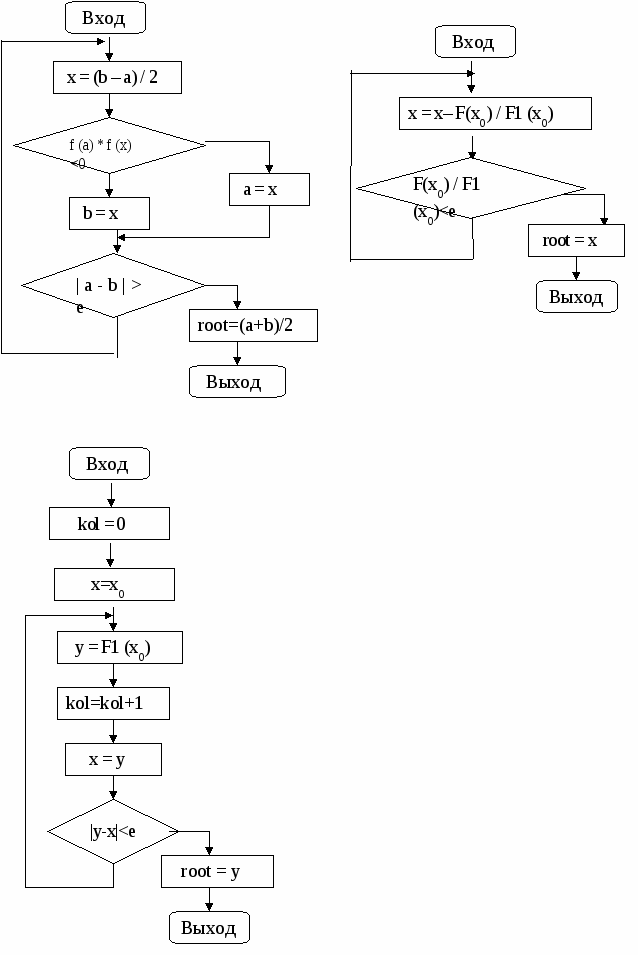 ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASICDECLARE SUB iter (x0!, e!, kol!, root!) DECLARE SUB iter (x0!, e!, kol!, root!) DECLARE SUB dix (a!, b!, e!, root!) DECLARE SUB kas (a!, b!, x!, e!, root!) DECLARE FUNCTION F! (x!) DECLARE FUNCTION G! (x!) DECLARE FUNCTION F1! (x!) DECLARE FUNCTION F2! (x!) DECLARE FUNCTION G2! (x!) REM численное решение не линейных уравнений 'уточнение корня методами касательных/дихот/ньютона/итерации CLS PRINT "проверка существования корня" PRINT " y = = x - 2 + SIN(1 / x)" REM ввод отрезка с проверкой на сущ решения DO INPUT "a= "; a INPUT "b= "; b INPUT "точность решения Eps="; e LOOP WHILE F(a) * F(b) > 0 REM мет дихотомии или метод деления отрезка пополам CALL dix(a, b, e, root) PRINT "корень ур по методу дихотомии="; root PRINT "значение функции F(x)="; PRINT USING " ##.######"; F(root) PRINT "-------------------------------------------" REM метод касательных или метод Ньютона INPUT "введите начальное значение корня на (a,b) X0="; x IF F(x) * F2(x) > 0 THEN PRINT "метод касательных(Ньютона) Применим" a = 1: b = 3 CALL kas(a, b, x, e, root) PRINT "корень по методу касательных="; root PRINT "значение функции F(x)="; PRINT USING " ##.######"; F(root) ELSE PRINT "метод касательных(Ньютона) НЕ Применим" END IF PRINT "-------------------------------------------" REM метод итерации INPUT "введите XO="; x0 IF ABS(G1(x)) < 1 THEN PRINT "метод Не применим" ELSE a = 1: b = 3 CALL iter(x0, e, kol, root) PRINT "корень по методу итерации="; root PRINT " количество итераций k="; kol PRINT "значение функции F(x)="; PRINT USING " ##.######"; F(root) END IF END SUB dix (a, b, e, root) x = (a + b) / 2 DO IF F(x) * F(a) < 0 THEN b = x ELSE a = x END IF x = (b + a) / 2 LOOP UNTIL (b - a) < e root = (b + a) / 2 END SUB FUNCTION F (x) F = x - 2 + SIN(1 / x) END FUNCTION FUNCTION F1 (x) F1 = 1 + COS(1 / x) END FUNCTION FUNCTION F2 (x) F2 = -SIN(1 / x) END FUNCTION FUNCTION G (x) G = 2 - SIN(1 / x) END FUNCTION FUNCTION G1 (x) G1 = -COS(1 / x) END FUNCTION SUB iter (x0, e, kol, root) kol = 0 x = x0 DO y = F1(x) kol = kol + 1 x = y LOOP UNTIL ABS(y - x) < e root = y END SUB SUB kas (a, b, x, e, root) DO x = x - F(x) / F1(x) LOOP UNTIL ABS(F(x) / F1(x)) < e root = x END SUB |
