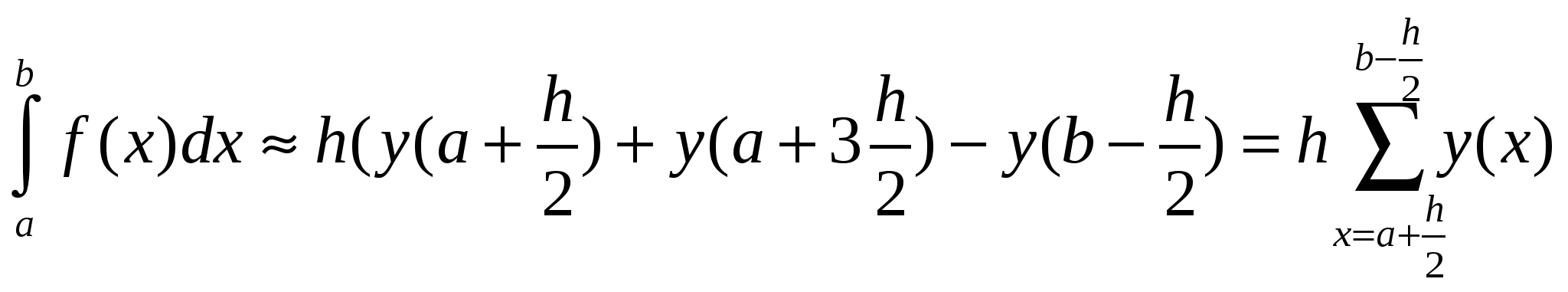|
|
Методич_стат-исправлено. Методические указания по курсу Информатика
БЛОК-СХЕМА
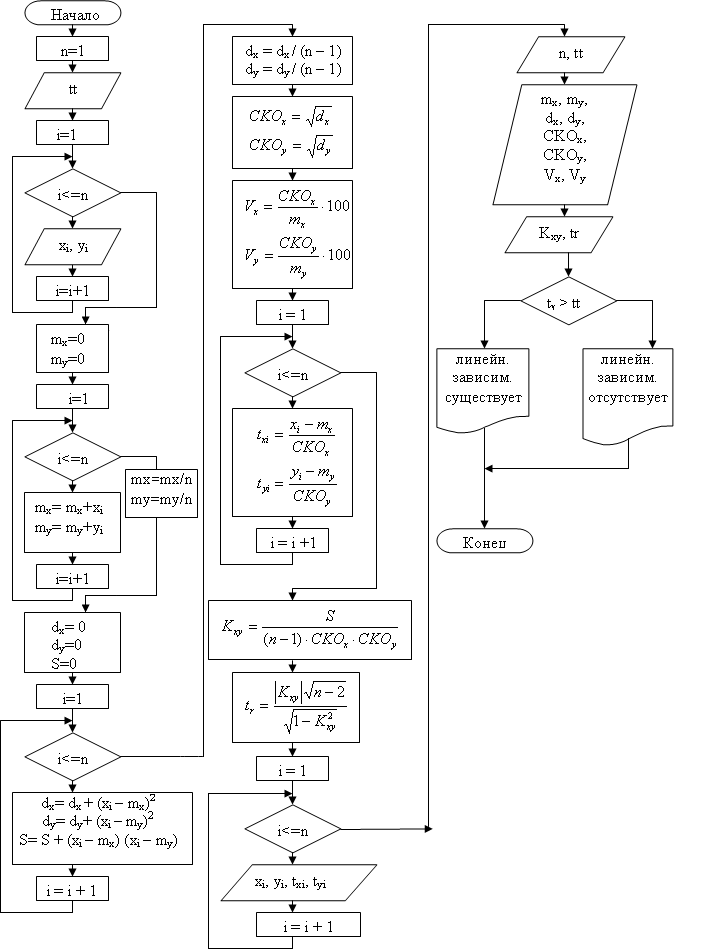
ПРОГРАММА НА ЯЗЫКЕ QBASIC
CLS
n = 11
INPUT "Введите Коэффициент Стьюдента="; tt
DIM x(1 TO n), y(1 TO n), tx(1 TO n), ty(1 TO n)
DATA 0.001, 0.002, 0.005, 0.01, 0.04, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5
FOR i = 1 TO n
READ x(i)
NEXT i
DATA 0.98, 0.97, 0.95, 0.92, 0.9, 0.84, 0.81, 0.8, 0.8, 0.81, 0.82, 0.84
FOR i = 1 TO n
READ y(i)
NEXT i
mx = 0: my = 0
FOR i = 1 TO n
mx = mx + x(i)
my = my + y(i)
NEXT i
mx = mx / n: my = my / n
dx = 0: dy = 0: S = 0
FOR i = 1 TO n
dx = dx + (x(i) - mx) ^ 2
dy = dy + (y(i) - my) ^ 2
S = S + (x(i) - mx) * (y(i) - my)
NEXT i
dx = dx / (n - 1): dy = dy / (n - 1)
CKOx = SQR(dx): CKOy = SQR(dy)
Vx = CKOx * 100 / mx: Vy = CKOy * 100 / my
FOR i = 1 TO n
tx(i) = (x(i) - mx) / CKOx
ty(i) = (y(i) - my) / CKOy
NEXT i
Kxy = S / ((n - 1) * CKOx * CKOy)
tr = ABS(Kxy) * SQR(n - 2) / SQR(1 - Kxy ^ 2)
PRINT " N", "x", "y", "tx", "ty"
FOR i = 1 TO n
PRINT i, x(i), y(i), tx(i), ty(i)
NEXT i
PRINT "число ответов ="; n
PRINT "табличное значение критерия Стьюдента ="; tt
PRINT "математическое ожидание :"; "по x="; mx, "по y="; my
PRINT "дисперсия :"; "по x="; dx, "по y="; dy
PRINT "среднеквадратическое отклонение :"; "по x="; CKOx, "по y="; CKOy
PRINT "коэффициент вариации :"; "по x="; Vx, "по y="; Vy
PRINT "коэффициент корреляции ="; Kxy
PRINT "рассчитанное значение критерия Стьюдента ="; tr
IF tr >= tt THEN
PRINT "линейная зависимость между x и y Cуществует"
ELSE
PRINT "линейная зависимость между x и y Отсутствует"
END IF
END
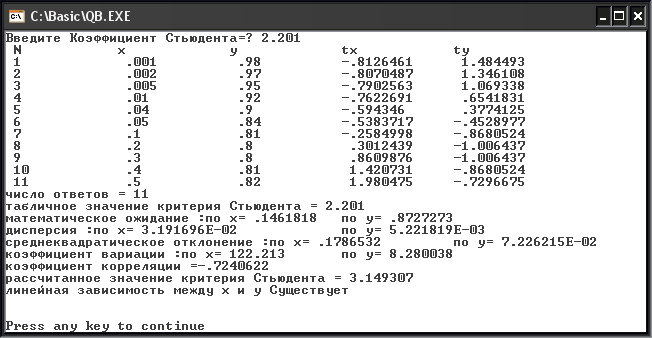
ПРИМЕР РАБОТЫ в EXCEL
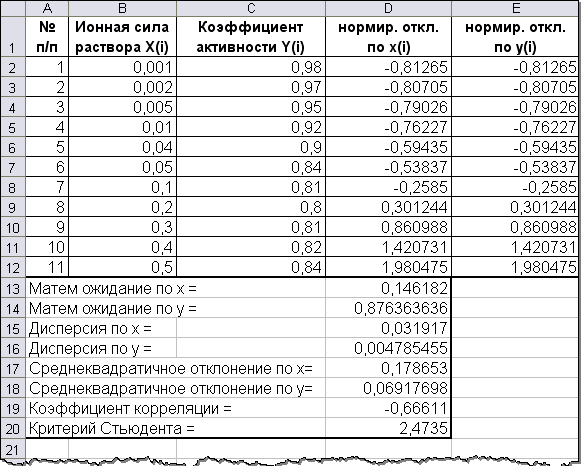
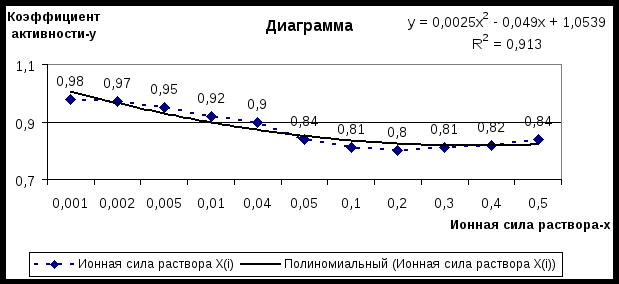
 Результаты эксперимента
Контрольные вопросы
«Статистическая обработка результатов эксперимента»
Что характеризует математическое ожидание?
Какие характеристики оценивают разброс случайных величин?
Как определяется дисперсия?
Для чего необходим коэффициент вариации?
Как определить нормированное отклонение?
Что характеризует коэффициент корреляции?
В каких пределах измеряется коэффициент корреляции?
Как определить уровень значимости коэффициента корреляции?
Как выбирается Ттабл?
Какое соотношение должно быть между Трасч и Ттабл, для утверждения, что линейная зависимость существует?
ЛАБОРАТОРНАЯ РАБОТА № 2
«Численное интегрирование» 1. Цель работы.
Ознакомится с принципом модульного программирования на примере задачи численного интегрирования. Использование оболочки QBASIC для построения процедур программ.
2. Основные теоретические сведения.
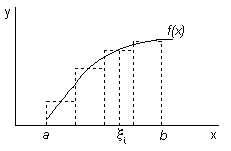
Пусть на отрезке [а,b] задана функция f(x). Определенный интеграл определяется как площадь, ограниченная подынтегральной функцией f(x), осью x и ординатами в точках «a» и «b»
Определенным интегралом от функции f(x) на отрезке [а, b] называется предел интегральной суммы при неограниченном увеличении числа точек разбиения.
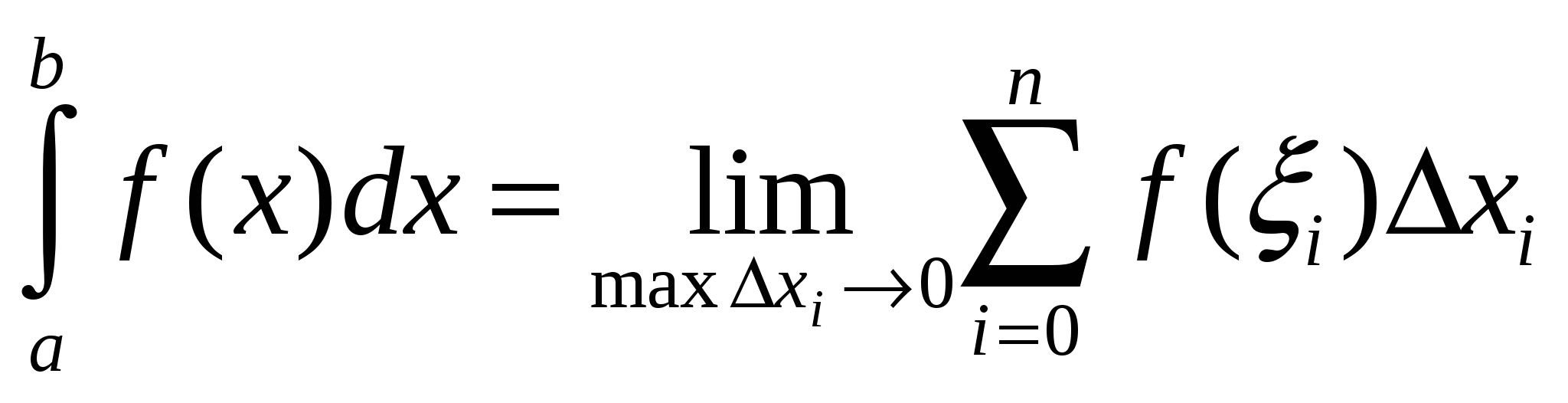
Во многих случаях, когда подынтегральная функция задана в аналитическом виде, определенный интеграл удается вычислить непосредственно по формуле Ньютона-Лейбница. Она состоит в том, что определенный интеграл равен приращению первообразной F(х) на отрезке интегрирования. На практике этой формулой часто нельзя воспользоваться по двум основным причинам:
Вид функции не допускает непосредственного интегрирования, т.е. первообразную нельзя выразить в элементарных функциях
Значения функций f(х) заданы таблично (множество хi конечно)
В этих случаях используются методы численного интегрирования.
Частным случаем в методах численного интегрирования является тот, когда величина элементарного отрезка ∆х,- величина постоянная и может быть вынесена за знак интегральной суммы. Эта величина называется шагом интегрирования и обозначается обычно ∆х.
Рассмотрим методы численного интегрирования.
В Методе прямоугольников непосредственно используется замена определенного интеграла интегральной суммой. В качестве точек xi; могут выбираться левые (xi-1) или правые (xi) границы элементарных отрезков. Расчетные формулы можно записать так:
При выборе левых границ (см. рис.1)
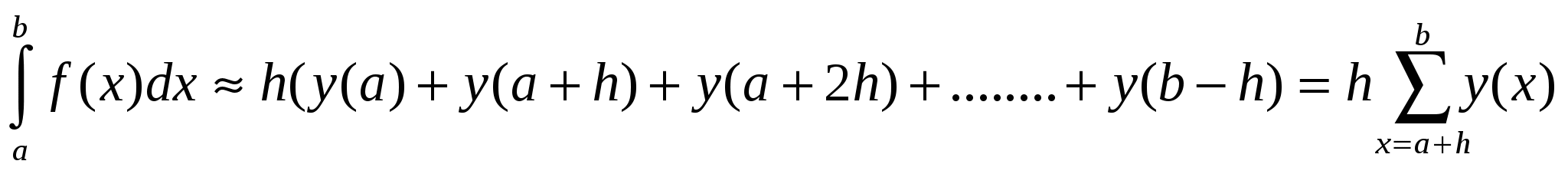
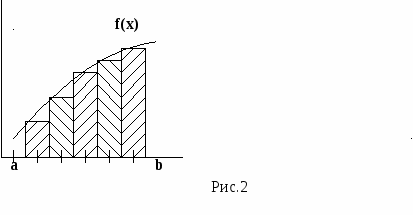
При выборе правых границ (см. рис.2)
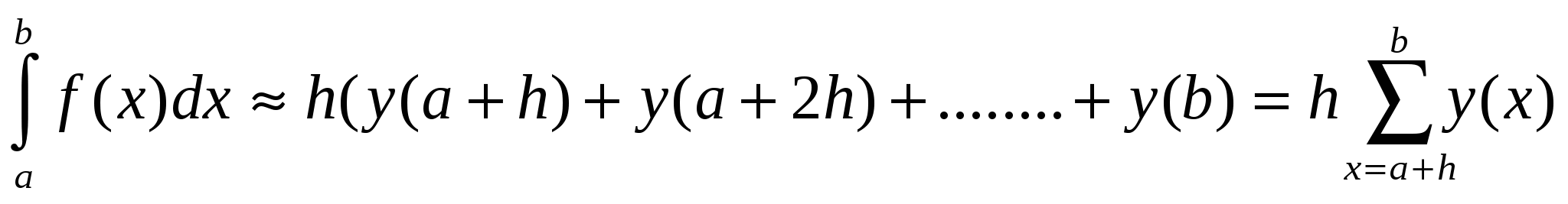
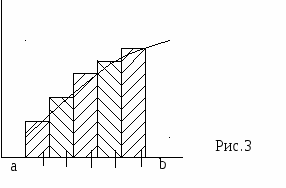
При выборе границ от a+ h/2 до b-h/2
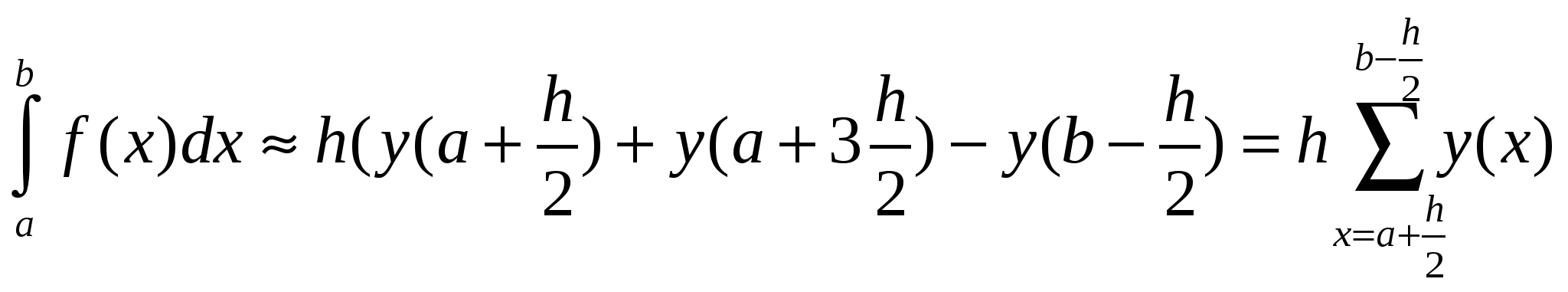
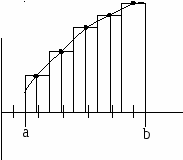
Рис.4
|
|
|
Скачать 2.11 Mb.
