Методические указания по проведению практических занятий для студентов 1 курса специальности 220501 Управление качеством

• Название: Методические указания по проведению практических занятий для студентов 1 курса специальности 220501 Управление качеством
• Анкор: metall
• Дата: 10.09.2022
• Размер: 313.26 Kb.
• Имя файла: met1.docx
• Тип: Методические указания; #670496
• страница: 3 из 8

Порог чувствительности прибора

Порог чувствительности прибора Лх - это есть минимальное изменение входного сигнала, которое может быть зарегистрировано (обнаружено, замечено) с помощью прибора без применения дополнительных технических средств.

Для приборов часто характерен гистерезис - (магнитный, электрический, механический), когда значения выходного сигнала y при одних и тех же значениях входного сигнала x не совпадают при прямом и обратном ходе. В этом случае статическая характеристика прибора имеет вид так называемой петли гистерезиса (см. рис. 4).

Причинами гистерезиса обычно являются: наличие трения в деталях прибора; наличие люфтов (зазоров) между деталями прибора.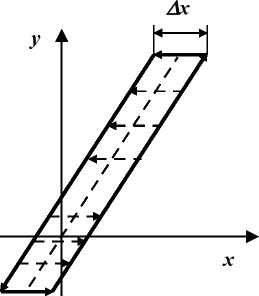


Рис. 4. Статическая характеристика прибора при наличии гистерезиса



Гистерезис является причиной существования порога чувствительности прибора и, как следствие, возникновения вариации показаний прибора. Гистерезис понижает точность измерений, поэтому желательно свести его к минимуму.

Аддитивные и мультипликативные погрешности

В зависимости от характера изменения величины погрешности при изменении измеряемой величины погрешности делятся на аддитивные и мультипликативные.

Аддитивные погрешности обусловлены смещением статической характеристики прибора вверх или вниз (вправо или влево), например, за счет смещения шкалы.

Влияние аддитивных погрешностей на статическую характеристику прибора показано на рис. 5.

Аддитивная погрешность (при выражении ее в виде абсолютной погрешности) имеет постоянную величину, не зависящую от значения измеряемой величины х:

Ay = y - y_u = k(x+Ax) - kx = kAx = const, т.к. k=const, Ax = const.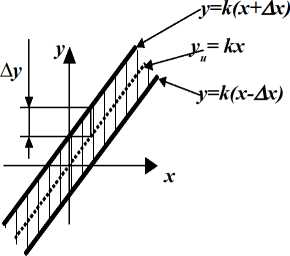



Рис. 5. Влияние аддитивных погрешностей на статическую характеристику прибора: y-и - идеальная статическая характеристика, y - фактическая статическая характеристика

При выражении аддитивной погрешности в виде относительной

погрешности получаем: 5y = Ay/y_u = kAx /kx = Ax /x = var, т.к. Ax=const, x= var.

Аддитивные погрешности преобладают у большинства стрелочных приборов.

Мультипликативные погрешности возникают из-за погрешностей задания передаточного коэффициента k статической характеристики y = kx.

Влияние мультипликативных погрешностей на статическую характеристику прибора показано на рис. 6.

Мультипликативная погрешность (при выражении ее в виде абсолютной погрешности) пропорциональная значению измеряемой величины:

Ay = y - y_u = (k+Ak)x - kx = Akx = var, т.к. Ak=const, x=var.

При выражении мультипликативной погрешности в виде относительной погрешности получим:

5y = Ay /Уи = Akx/ kx = Ak / k = const, т.к. Ak=const, k=const, т.е. у приборов с преобладающими мультипликативными погрешностями постоянной остается относительная погрешность.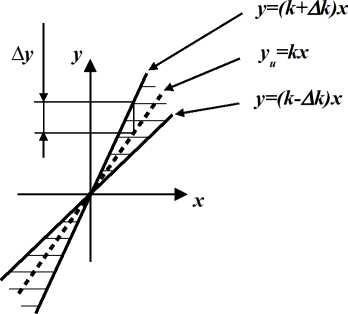



Рис. 6. Влияние мультипликативных погрешностей на статическую характеристику прибора: уи - идеальная статическая характеристика; y - фактическая статическая характеристика.

Мультипликативные погрешности преобладают у приборов, относящихся к масштабирующим преобразователям (шунты, добавочные сопротивления, усилители, делители, трансформаторы и т.п.).

Основные и дополнительные погрешности приборов

По влиянию внешних условий различают основную и дополнительную погрешности средства измерений.

Основной называется погрешность средства измерений, определяемая в нормальных условиях его применения. Для каждого средства измерений в нормативно-технических документах оговариваются условия эксплуатации - совокупность влияющих величин (температура окружающей среды, влажность, давление, напряжение, частота питающей сети и др.), при которых нормируется его погрешность (влияющая величина - это физическая величина, не измеряемая данным средством измерений, но оказывающая влияние на его результаты).

Пример задания основной погрешности в нормативно-технической документации.

Для вискозиметра автоматического ротационного типа ВАР-5Ж пределы допускаемой основной приведенной погрешности канала измерения вязкости по показаниям и выходному непрерывному сигналу равны ±2,5% от диапазона измерения при следующих нормальных условиях:

1. 
   температура окружающего воздуха (20±5)°С;
   
2. 
   относительная влажность окружающего воздуха до 80%;
   
3. 
   атмосферное давление от 84 до 106,7 кПа;
   
4. 
   температура анализируемой среды от 20 до 30 °С;
   
5. 
   давление анализируемой среды отсутствует;
   
6. 
   отклонение напряжения питания не более ±2% от номинального;
   
7. 
   отсутствие вибрации и ударов;
   
8. 
   длина линии связи между первичным преобразователем и измерительным блоком не более 10 м;
   
9. 
   движение анализируемой среды относительно первичного преобразователя отсутствует.
   

Дополнительной называется погрешность средства измерений, возникающая вследствие отклонения какой-либо из влияющих величин, т.е дополнительная погрешность, увеличивающая общую погрешность прибора, возникает, если прибор работает в условиях, отличных от нормальных.

Пример задания дополнительной погрешности в нормативно-технической документации.

Для вискозиметра автоматического ротационного типа ВАР-5Ж дополнительные погрешности в долях предела основной допускаемой погрешности (ОДП) канала измерения вязкости не превышают:

1. 
   0,5 предела ОДП, вызванной отклонением напряжения питания измерительного блока на плюс 10 минус 15 % от номинального;
   
2. 
   0,5 предела ОДП, вызванной отклонением температуры окружающего воздуха от нормальной на каждые 10 °С в пределах (5^50) °С;
   

Класс точности - это обобщенная характеристика средства измерений, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность.

Основные способы задания класса точности средств измерений.

Существует несколько способов задания классов точности приборов.

1. 
   способ используется для так называемых мер (мера - средство измерений, предназначенное для воспроизведения физической величины заданного размера; например, гиря - мера массы, температурная лампа - мера яркости, нормальный элемент - мера электродвижущей силы и напряжения). При этом способе указывается порядковый номер класса точности меры. Например, нормальный элемент 1 класса точности, набор разновесов (гирь) 2 класса точности и т.п. Порядок вычисления погрешностей в этом случае определяют по технической документации, прилагаемой к мере.
   
2. 
   способ предусматривает задание класса точности для приборов с преобладающими аддитивными погрешностями. В этом случае класс точности задается в виде числа К (без кружочка). При этом нормируется основная приведенная погрешность ух прибора, выраженная в процентах, которая во всех точках шкалы не должна превышать по модулю числа К,
   

т.е. |yx|<К, %.

Число К выбирается из ряда значений (1,0;1,5;2;2,5;4,0;5,0;6,0) ■ 10n , где n = 1, 0, -1, -2...

3. 
   способ предусматривает задание класса точности для приборов с преобладающими мультипликативными погрешностями. В этом случае нормируется основная относительная погрешность, выраженная в процентах, так что
   

|SХ|<К, %.

Класс точности задается в виде числа К в кружочке ® .

Число К выбирается из приведенного выше ряда.

4. 
   способ предусматривает задание класса точности для приборов с соизмеримыми аддитивными и мультипликативными погрешностями. В этом случае класс точности задается двумя числами a/b, разделенными косой чертой, причем a>b. При этом нормируется основная относительная погрешность, вычисляемая по формуле:
   

|SX| < [a + b-(|X_K/X| - 1)], %,

где Х_к - максимальное конечное значение пределов измерений.

Число a отвечает за мультипликативную составляющую погрешности, а число b - за аддитивную составляющую погрешности. Значения a и b выбираются из вышеприведенного ряда.

5. 
   способ задания класса точности используется для приборов с резко неравномерной шкалой. Класс точности задается числом К, подчеркнутым галочкой К- . В этом случае нормируется основная приведенная погрешность в процентах от длины шкалы.
   

Литература:

1. Мищенко, С.В. История метрологии, стандартизации, сертификации и управления качеством: Учебное пособие / Сост. С.В. Мищенко, С.В. Пономарев, Е.С. Пономарева, Р.Н. Евлахин, Г.В. Мозгова. - Тамбов : Тамбовск. гос. техн. ун-т, 2004. - 94 с.