|
|
Методические указания по проведению практических занятий для студентов 1 курса специальности 220501 Управление качеством
Предварительные сведения из математики
Понятие дифференциала. Если приращение функции y=f(x) представить в виде: Лу=АЛх+а, где А не зависит от Лх, а а имеет более высокий порядок относительно Лх (при Лх^0), то величина АЛх называется дифференциалом функции f(x) и обозначается dy или df(x).
Пример: y=x2.
Лу=(х+Лх)2-х2=х2+2хЛх+Лх2-х2=2хЛх+Лх2.
В данном случае dy=2xЛx - дифференциал, а а=Лх2.
Графически дифференциал представляет собой приращение ординаты касательной (см. рис. 1).
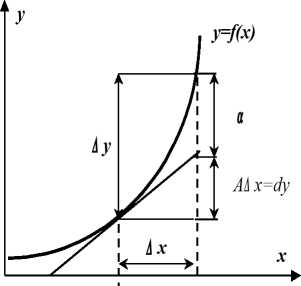
Рис. 5.15. Геометрический смысл дифференциала
Свойства дифференциала.
Постоянный множитель можно вынести за знак дифференциала: d [ af(x )]= ad [fx)], где a=const.
Дифференциал суммы равен сумме дифференциалов:
d[f1(x)+f2(x)-f3(x)]=d[f1(x)]+d[f2(x)]-d[f3(x)].
Дифференциал функции равен произведению производной на дифференциал аргумента: df(x) = d (x) dx = f (x)dx.
dx
Дифференциал логарифма переменной величины dln(x) = dln(x)dx = dx.
dx x
Методики получения формул для вычисления погрешностей косвенных
измерений по известным погрешностям прямых измерений
Получение формул для вычисления погрешностей косвенных измерений в случае зависимости вида Y = a + b - c (сумма, разность)
Исходные данные: a,b,c, A a, A b, A c.
Вывод формул для вычисления погрешностей косвенных измерений в рассматриваемом случае можно выполнить следующим образом.
Найдем дифференциал правой и левой части
dY = d(a+ b- c) = da+ db- dc .
Произведем широко используемую в теории погрешностей замену дифференциалов абсолютными погрешностями (при условии, что абсолютные погрешности достаточно малы) dY
A Y,da
A a,db
A b,dc
A c.
Тогда A Y = A a + A b - A c .
Учитывая, что знаки погрешностей A a, A b, A c обычно бывают заранее неизвестны, для получения гарантированной (предельной) оценки абсолютной погрешности косвенного измерения в последней формуле все знаки "-" заменим на знаки "+"
AY =Aa+Ab+Ac пр .
Найдем предельную оценку относительной погрешности косвенного
измерения, учитывая, что относительная погрешность есть отношение абсолютной погрешности к результату измерений:
AY Aa+ Ab+ Ac
пр = Y = a + b - c ’
Величина предельной погрешности во многих случаях бывает завышенной, поэтому часто применяют среднеквадратические оценки погрешности. Для получения среднеквадратической оценки погрешности в формуле для предельной оценки погрешности сумму заменяют корнем квадратным из суммы квадратов.
Найдем среднеквадратические оценки абсолютной и относительной погрешностей косвенного измерения:
A Y. = V(A a)2 + (A b)2 + (A c)2 ;
 
Y a+b-c
§ YCK ск
A Y«, 7(A a)2 + (A b)2 + (A c)2
Получение формул для вычисления погрешностей косвенных
измерений в случае зависимости вида Y = acb (произведение, деление).
Исходные данные: a,b,c, A a, A b, A c.
Вывод формул для вычисления погрешностей косвенных измерений в рассматриваемом случае можно выполнить следующим образом.
Прологарифмируем левую и правую части заданной зависимости:
lnY = ln a—- = lna + Inb- Inc .
c
Найдем дифференциал правой и левой частей:
dlnY = dln a—- = dlna + dlnb - dlnc . c
Учитывая, что дифференциал от логарифма переменной величины находится по формуле: d(lnx) = ^x ■ dx = —, получаем:
dx x
dY da db dc
— = — + —.
Yabc
Произведем широко используемую в теории погрешностей замену дифференциалов малыми абсолютными погрешностями (при условии, что абсолютные погрешности достаточно малы):
dY « A Y,da « A a,db « A b,dc « A c .
AY Aa Ab Ac
Тогда — = —+ — .
Yabc
Учитывая, что знаки погрешностей Aa,Ab,Ac заранее неизвестны, для получения гарантированной (предельной) оценки относительной погрешности косвенного измерения в последней формуле все знаки "-" заменяем на знаки "+":
 
или § Ynp
(AY
Y
пр
Aa Ab Ac
= —+ —+ — abc
Предельную оценку абсолютной погрешности косвенного измерения находим по формуле:
AY = §Y ■Y пр пр .
Величина предельной погрешности во многих случаях бывает завышенной, поэтому часто применяют среднеквадратические оценки погрешности. Для получения среднеквадратической оценки погрешности в формуле для предельной оценки погрешности сумму заменяют корнем
квадратным из суммы квадратов.

> a)2 +(§ b)2 +(§ c)2 .
f A a 1
(
|
2
_L
+
|
1 —
|
2
_L
+
|
'Ac'
|
2
|
I a J
|
|
[b
|
|
tcJ
|
| Найдем среднеквадратические оценки относительной и абсолютной погрешностей косвенного измерения:
A YrK = i
|
(A« 1
|
2
|
fAb1
|
2
|
fAc1
|
2
|
|
+
|
|
+
|
|
■ Y =
|
ck Д
|
taJ
|
tbJ
|
tcJ
|
ck
§Y
д/(§ a)2 + (§ b)2 + (§ c)2 ■ Y
|
|
|
 Скачать 313.26 Kb.
Скачать 313.26 Kb.





