лое. Лое. Методические указания по проведению практических занятий по метрологии и измерительной технике для студентов всех специальностей очной формы обучения

• Название: Методические указания по проведению практических занятий по метрологии и измерительной технике для студентов всех специальностей очной формы обучения
• Дата: 19.04.2023
• Размер: 1.9 Mb.
• Имя файла: Лое.doc
• Тип: Методические указания; #1074351
• страница: 10 из 12

4.4. Электронно-лучевые осциллографы
4.4.1. Вопросы для самоконтроля

4. 
   
   

1) Назначение электронно-лучевого осциллографа, как средства измерений, его основные характеристики.

2) Канал вертикального отклонения осциллографа (канал Y ). Основные блоки канала и их назначение.

3) Канал горизонтального отклонения (канал X ), основные блоки и их назначение.

4) Канала Z осциллографа и его назначение.

5) Что означает термин «развертка исследуемого сигнала»? Какие виды разверток используются в электронном осциллографе?

6) Что означает термин «синхронизация развертки»? В чем проявляется отсутствие синхронизации? Что физически означает понятие «синхронизация развертки осциллографа осуществлена»? В чем это проявляется?

7) Какие виды синхронизации используются в осциллографе? Как осуществляется тот или другой вид синхронизации?

8) Что такое «режим периодической линейной развертки с внутренней (или внешней) синхронизацией»? Как осуществляется этот режим (перечислить порядок действий для осуществления этого режима работы)? Когда используется этот режим работы?

9) Что такое «режим ждущей линейной развертки с внутренней (или внешней) синхронизацией»? Чем он отличается от режима периодической линейной развертки? Как осуществляется этот режим работы осциллографа (перечислить порядок действий по осуществлению этого режима)? В каких случаях используется этот режим?

10) Как реализуется режим синусоидальной развертки? Почему он так называется? Для измерения каких параметров сигналов и каким образом можно использовать этот режим работы осциллографа?

11) Что такое «режим наблюдения интерференционных фигур»? Как он реализуется? Для каких измерений можно использовать этот режим?

12) Что означают понятия «коэффициент отклонения канала Y» и «калиброванный коэффициент отклонения канала Y ( )», в чем отличие этих понятий? Как реализуется калиброванный коэффициент отклонения?

13) Что означают понятия «коэффициент развертки» и «калиброванный коэффициент развертки ( )»? Как реализуется калиброванный коэффициент развертки?

14) Как осуществляется измерение напряжения сигнала с помощью осциллографа (перечислить все действия по подготовке осциллографа к измерению напряжения и по определению величины измеряемого напряжения)?

15) Как осуществляется измерение временных интервалов с помощью осциллографа (перечислить все действия по подготовке осциллографа к измерению временных интервалов и по определению длительности измеряемого интервала)?

16) Какие условия необходимо выполнить, чтобы при определении погрешности результатов измерения напряжения (или интервалов времени) можно было пользоваться такой метрологической характеристикой осциллографа, как «предел допускаемой основной погрешности», приводимой в техническом описании?

17) Как определять погрешность результатов, если по условиям измерений метрологическую характеристику - «предел допускаемой основной погрешности» использовать нельзя? Объясните, когда возникают такие условия?

18) Как с помощью осциллографа осуществляется измерение коротких интервалов времени (таких, например, как время нарастания сигнала)? Перечислить все действия по подготовке осциллографа к измерениям и по определению временного интервала.

19) При измерении коротких временных интервалов с помощью осциллографа могут появляться методические погрешности. Каковы физические причины появления этих погрешностей? Каким образом результат можно исправить?

20) Почему при измерении коротких интервалов времени надо использовать штатные соединительные кабели (соединительные кабели из комплекта принадлежностей, поставляемых заводом изготовителем вместе с осциллографом)? Почему нельзя использовать любой другой, подходящий по разъемам, соединительный кабель?


4.4.2. Примеры решения задач
Задача № 4.10

Определить амплитуду U_m синусоидального сигнала по изображению на экране осциллографа, если отклонение луча по вертикали - l_Y, соответствующее размаху напряжения (размах – величина напряжения сигнала от пика до пика ), равно 5 делениям масштабной сетки, значение коэффициента отклонения , а значение множителя коэффициента отклонения .
Решение:

Величина размаха напряжения синусоиды определяется по формуле

U_р = K_y  M_y l_Y = 0,5  1  5 = 2,5 В.

Амплитуда синусоиды равна половине размаха, т.е.

.
Задача № 4.11

Определить длительность прямоугольного импульса по изображению на экране осциллографа, если отклонение луча l_X по горизонтали, соответствующее длительности импульса (на уровне 0,5), равно 4 делениям масштабной сетки, значение коэффициента развертки , а множитель развертки M_р = 0,1.
Решение:

Длительность импульса определяется выражением
 = K_р M_р l_X = 0,5  0,1  4 = 0,2 мкс.
Задача № 4.12

Определить длительность импульса и частоту однополярного прямоугольного импульсного сигнала, если его изображение на экране осциллографа имеет вид :

Коэффициент развертки , а множитель развертки
М _р= 0,5.
Решение:

В данном случае для измерения временных интервалов используется метод калиброванной развертки. Тогда длительность импульса _u и частота f сигнала определяются выражениями:
_u = К_р · М_р · l_u , _,

где l_u и l_Т  отрезки, соответствующие значениям длительности импульса и его периода в делениях масштабной сетки.
В соответствии с рисунком l_u = 2 дел, а Т = 6 дел.

Тогда: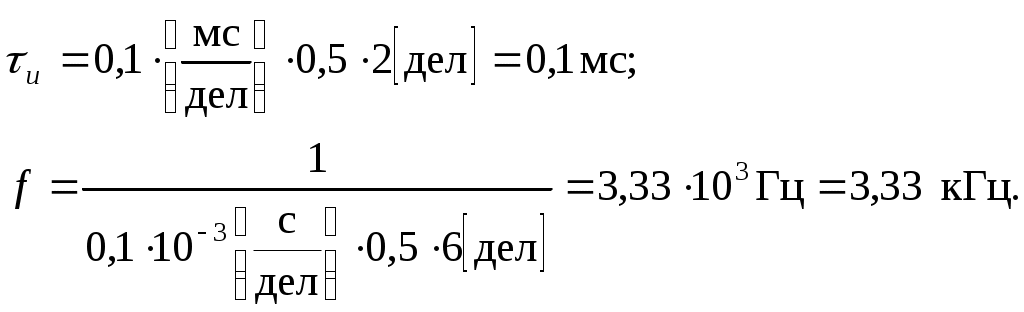

Задача № 4.13

В режиме линейной развертки на экране двухлучевого осциллографа наблюдается изображение следующего вида: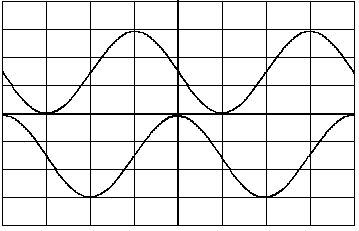


Определить фазовый сдвиг между сигналами, если коэффициент развертки - .
Решение:

Фазовый сдвиг при линейной развертке определяется выражением ,

где: ΔТ  временный сдвиг, между одинаковыми характерными точками обоих сигналов; Т  период сигналов.

Наиболее точно можно выделить на сигналах точки перехода через ноль в область положительных или отрицательных значений. В соответствии с рисунком интервалу соответствует одно деление масштабной сетки, а периоду Т – 4 деления.

Следовательно в нашем случае:

;
;
искомый фазовый сдвиг
.
Примечание. Так как в формуле для определения используется отношение величин ΔТ и Т, а коэффициент развертки Кр при измерении этих величин одинаков, то для расчета можно использовать значение ΔТ и Т выраженные в делениях масштабной сетки осциллографа и не вычислять эти величины в единицах времени.

Задача № 4.14

Для точного измерения временных интервалов импульсного сигнала, поданного на вход Y , на вход Z осциллографа подано напряжение образцового генератора в виде коротких импульсов положительной полярности с периодом Т_z = 1 мкс. Определить длительность исследуемого импульсного сигнала и его период, если изображение на экране осциллографа имеет вид:

Точками изображены яркостные отметки на изображении исследуемого сигнала, возникающие под воздействием импульсного сигнала, поданного на вход Z. При этом расстояние между двумя яркими точками соответствует длительности периода сигнала на входе Z , т.е. - Т_{z .}
Решение:

В том случае, когда для получения яркостных меток на изображении исследуемого сигнала на вход Z подается сигнал известной частоты, величина измеряемого интервала определяется числом яркостных меток, укладывающихся в этот интервал

t_x = nT_z ,

где n  число меток.
В нашем случае, при определении длительности импульса нетрудно подсчитать, что n_и = 12, а для периода сигнала  n _Т = 16.
Тогда:

_u· = n_u · T_z = 121 [ мкс ] = 12[ мкс ];
T = n_T · Т_z = 16 ·1 [ мкс ] = 16 [ мкс ].
Задача № 4.15

На э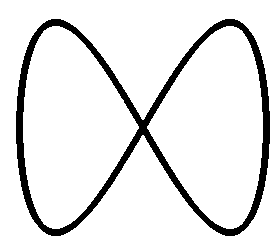кране осциллографа при измерении частоты методом фигур Лиссажу (режим синусоидальной развертки) получено неподвижное изображение следующего вида:
Y


X


Определить частоту сигнала, поданного на вход Y осциллографа, если частота сигнала, поданного на вход X равна 1 кГц.
Решение:

Кратность частот в данном случае определяют по числу пересечений неподвижной фигуры с горизонтальной - п_х и вертикальной - п_у линиями в соответствии с формулой . При этом линии необходимо располагать на фигуре так, чтобы число пересечений каждой из них было максимально возможным. В нашем случае п_х=4, п_у=2.

Тогда искомая частота .
Задача № 4.16

На экране осциллографа при измерении частоты методом круговой развертки (частный случай синусоидальной развертки) получено следующее изображение: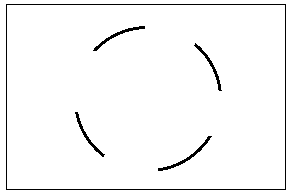


Определить частоту исследуемого сигнала, напряжением которого осуществлена круговая развертка, если частота образцового сигнала, поданного на модулятор ЭЛТ (вход Z), равна 1000 Гц.
Решение:

Для получения круговой развертки на входы Х и У осциллографа поданы синусоидальные напряжения неизвестной но одинаковой частоты, сдвинутые друг относительно друга на 90⁰. При этом полный круг луч описывает за время, соответствующее одному периоду этих сигналов. При подаче на вход Z сигнала известной частоты изображение круга на экране (при условии кратности частот) представляет собой чередование неподвижных ярких и темных меток. При этом время, за которое луч пробегает участок окружности, соответствующий яркой и темной меткам, равен периоду сигнала на входе Z.

Следовательно неизвестная частота сигнала на входах X и Y осциллографа может быть определена по количеству ярких (или темных) меток, укладывающихся в изображении окружности на экране.

В данном случае п = 4 и

_.
Задача № 4.17

Электронным осциллографом исследуется импульсный сигнал. Известно, что собственное время нарастания переходной характеристики усилителя канала вертикального отклонения _нy = 0,05 мкс. Определить верхнюю частоту полосы пропускания усилителя канала Y и длительность фронта исследуемого сигнала, если известно, что относительная погрешность измерения длительности фронта импульса по изображению на экране осциллографа составляет _ф = 15%.
Решение:

Сначала найдем верхнюю частоту полосы пропускания f_вy канала вертикального отклонения осциллографа. Известно, что время нарастания _нy и f_вy связаны между собой следующим соотношением:

,

тогда .
Величина фронта импульса, измеренная по изображению на экране осциллографа _{ф осц}представляет собой геометрическую сумму реального фронта импульса _ф (на входе осциллографа) и собственного времени нарастания _нy канала Yосциллографа, т.е.
.
Но определить искомую величину _ф непосредственно из этого выражения не удается, т.к. в нем известна только одна величина _нy. Необходимо использовать дополнительные данные из условия задачи. Относительная погрешность измерения физической величины по определению

,

где x_изм - измеренное значение физической величины X,

x_ист - истинное (действительное) значение измеряемой величины.
Если это определение интерпретировать к нашей задаче, то можно записать

_.

Величина относительной погрешности измерения нам известна. В этом случае для определения искомой величины _ф необходимо решить систему уравнений с двумя неизвестными: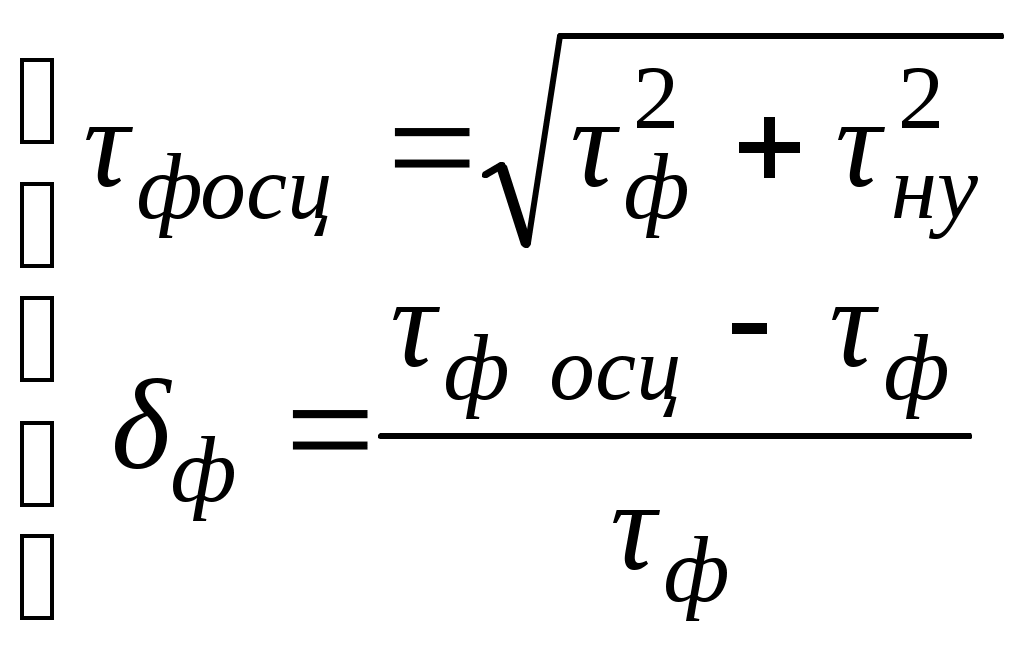
.

Выражая величину _{ф осц}через величины _ф и _ф:
_{ф осц} = _ф + _ф_ф = _ф (1+_ф)
первое уравнение можем записать в следующем виде:
.
Решаем систему уравнений относительно _ф: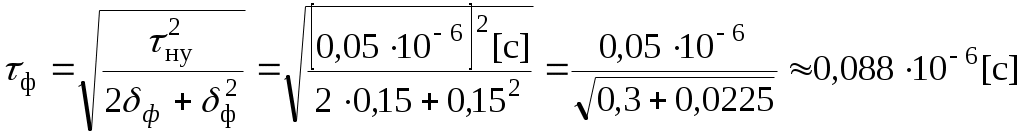
; ;
.
Ответ: f_вy= 7 МГц; _ф = 0,088 мкс.
Аналогичным образом решаются задачи рассмотренного типа при различных вариантах задания исходных величин _ф , _{ф осц} , _нy, f_{вy .}