лое. Лое. Методические указания по проведению практических занятий по метрологии и измерительной технике для студентов всех специальностей очной формы обучения

• Название: Методические указания по проведению практических занятий по метрологии и измерительной технике для студентов всех специальностей очной формы обучения
• Дата: 19.04.2023
• Размер: 1.9 Mb.
• Имя файла: Лое.doc
• Тип: Методические указания; #1074351
• страница: 4 из 12

Обработка результатов косвенных измерений.

1) В чем состоит специфическая особенность косвенных измерений?

2) Приведите классификацию косвенных измерений.

3) Какой прием используется для решения задачи о погрешности результата косвенных измерений? При каких условиях использование его правомерно?

4) Какие условия должны выполняться, чтобы при определении погрешности можно было использовать линейное приближение разложения исходной функции в ряд?

5.)Что такое коэффициент влияния? Что он определяет?

6) Как определяется значение коэффициента влияния? Какое числовое значение может он иметь?

7) В чем особенность суммирования составляющих погрешностей аргументов при определении систематической и случайной погрешностей результата косвенных измерений?

8) Как определяется общая погрешность результата косвенных измерений?
2.5.2. Примеры решения задач

Задача № 2.12

Обработка результатов, полученных при поверке образцового резистора класса 1,0 с номинальным значением 10 Ом, дала следующие результаты:

Ом; Ом; Ом.

Представить результат измерения с указанием общей погрешности. Исходя из пределов общей погрешности сделать вывод, соответствует ли резистор своему классу точности.

Решение.

1. В соответствии с рекомендациями ГОСТ 8.207-76 для определения границ общей погрешности определяем сначала величину отношения (см. стр. 67 – 69 [4] ).

Для условий задачи отношение .

Так как 0,8   8, то 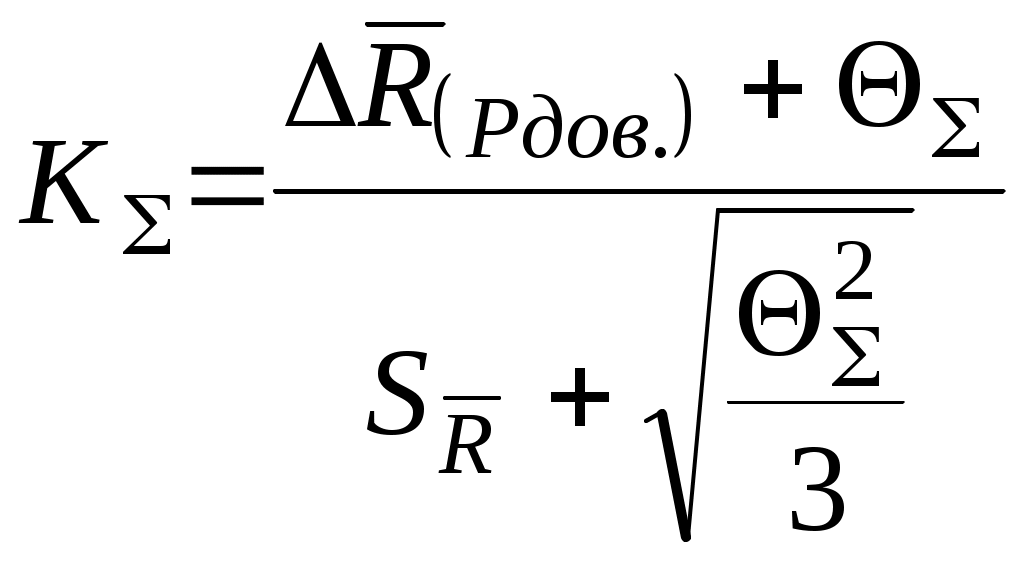(в соответствии с рекомендациями стандарта) границы общей погрешности вычисляем по формуле:

,

где ;

.

Учитывая, что класс точности образцовых резисторов присваивается по величине предельного отклонения, границы доверительного интервала случайной погрешности определим при .

Ом.

2. Определяем величины 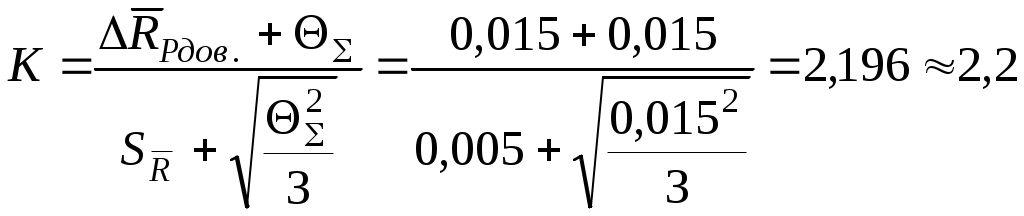и :

;

Ом;

Ом.

3. Так как Ом (по условию задачи), а границы общей погрешности образцового резистора Ом, то действительное значение поверяемого образцового резистора находится в границах:

10,038 Ом  R  10,082 Ом.

Согласно требованиям на образцовые меры электрического сопротивления, относительное отклонение действительного значения меры от номинального значения не должно превышать значения, численно равного обозначению класса точности.
4. Определяем предельное относительное отклонение образцового резистора от номинала

%  1%.

Ответ: действительное значение образцового резистора находится в границах 10,038 Ом  R  10,082 Ом; по результатам поверки образцовый резистор соответствует своему классу точности.
Задача № 2.13

В цепь с током 15А включены три амперметра:

А1 класса точности 1,0 со шкалой на 50 А;

А2 класса точности 1,5 со шкалой на 30 А;

А3 класса точности 2,5 со шкалой на 20 А.

Определить, какой амперметр обеспечит большую точность измерения тока?
Решение:

Ответить на вопрос задачи можно, сравнив между собой величины абсолютных или относительных погрешностей. Для СИ, у которых преобладает аддитивная погрешность, удобнее сравнивать абсолютные погрешности, поскольку они постоянны по всей шкале. Условное обозначение классов точности (1,0; 1,5; 2,5) говорит о том, что для всех трех амперметров преобладает аддитивная погрешность, которая определяется для соответствующего прибора соотношением , где  класс точности, а конечное значение шкалы (предел измерения см. табл. 3.1 [4] ).

Следовательно:

(А);

(А);

(А).

Ответ:

Большую точность измерения тока обеспечит второй амперметр.

Задача № 2.14

Можно ли определить величину измеряемого напряжения, если известно, что оно измерено с относительной погрешностью % прибором с пределом измерения В, а класс точности имеет на шкале условное обозначение вида ?

Решение:

При таком условном обозначении класса точности относительная погрешность результата измерения определяется выражением (см. табл. 3.1 [4]):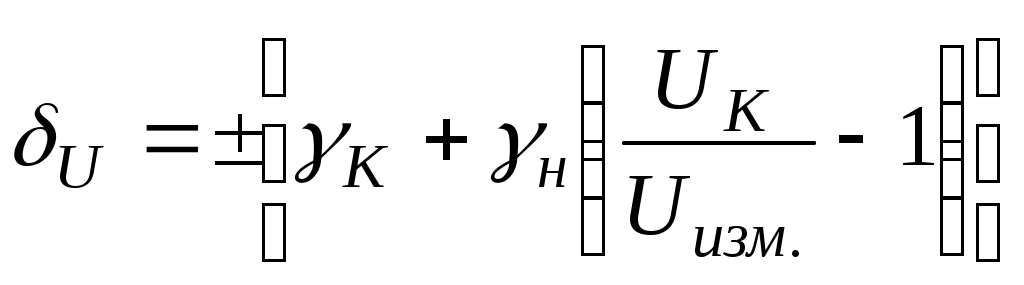

%.

Следовательно, можем записать: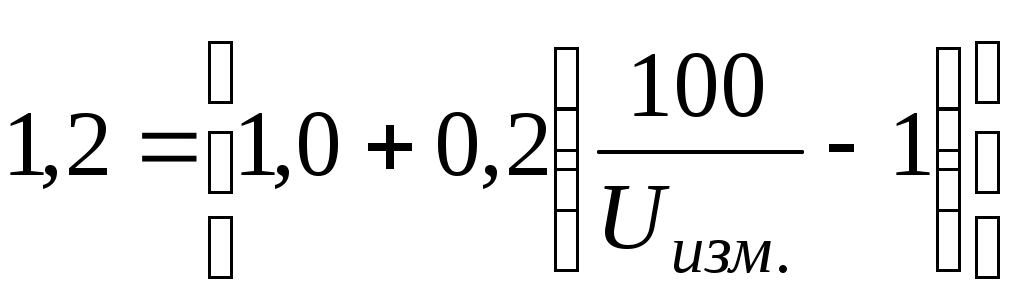

, откуда В.

Ответ: Можно, В.
Задача № 2.15

Необходимо выполнить однократное измерение падения напряжения на участке цепи с погрешностью, не превышающей %.
Априорные данные об исследуемом объекте и условиях проведения измерительного эксперимента:

Участок цепи представляет собой стабильное сопротивление Ом;

Ток в цепи постоянный;

Измерение проводится в сухом отапливаемом помещении при температуре до +30С и напряженности внешнего магнитного поля до 300 А/м;

Предполагаемое падение напряжения на участке цепи постоянно и не превышает 1,5 В.

Для измерений выбран вольтметр класса точности 0,5 с верхним пределом измерения В. Показания вольтметра при измерении В.

При изучении метрологических характеристик вольтметра по техническому описанию установлено, что:

Внутреннее сопротивление вольтметра Ом, %.

Нормальные условия эксплуатации следующие:

температура окружающего воздуха С;

напряженность внешнего магнитного поля А/м;

дополнительная температурная погрешность не превышает основной, при отклонении температуры от нормальной на каждые 10С;

дополнительная погрешность, обусловленная отклонением внешнего магнитного поля от нормальной не превышает половины основной, при отклонении напряженности внешнего магнитного поля от нормальной на каждые 100 А/м.

Решение:

1. Известно, что при измерении напряжения методическая погрешность определяется соотношением между сопротивлением участка цепи и сопротивлением вольтметра . Методическая погрешность в относительной форме определяется соотношением

%.

Очевидно, что если напряжение должно быть измерено с погрешностью не более %, то в результат измерения необходимо внести поправку на методическую погрешность.

Величина поправки в абсолютной форме определяется по формуле

(В).

Тогда с учетом поправки результат измерения будет

(В).

Поскольку и известны с погрешностями, то введением поправки не удается полностью исключить методическую погрешность, неисключенный остаток методической погрешности определяется погрешностями % и %. Границы неисключенного остатка методической погрешности можно оценить, зная что:

; %; %.

Оценка границ неисключенного остатка методической погрешности дает результат %. (Оценка границ неисключенного остатка методической погрешности в данной задаче не рассматривается, так как для этого необходимо воспользоваться правилами определения погрешности результата косвенных измерений. Определение границ неисключенного остатка методической погрешности приводится в решении задачи № 2.17).
2. Определяем границы основной погрешности результата измерения

%.

3. Определяем границы дополнительной температурной погрешности

%.

4. Определяем границы дополнительной погрешности от влияния внешнего магнитного поля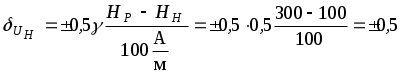

%.

5. Сравнивая границы неисключенного остатка методической погрешности с границами основной и дополнительных погрешностей, делаем вывод, что величина пренебрежимо мала, по сравнению с другими погрешностями и ее можно не учитывать. Принимая во внимание, что все составляющие погрешности измерения напряжения получены через класс точности вольтметра в виде границ, а о виде закона распределения каждой из составляющих достоверных сведений нет, границы погрешности результата находим по формуле (2.35 [4] ), задав доверительную вероятность и записав формулу для относительных погрешностей в виде:

%.

Учитывая, что число составляющих погрешности мало, оценим арифметическую сумму их

%.

Так как  , то в качестве границ погрешности результата измерения принимаем доверительные границы при .

6. Доверительные границы в абсолютной форме

(В).

Следовательно, результат измерения в окончательном виде можно представить в форме:

В; В; или

В; .

Ответ: В; .

Задача № 2.16

Мощность Р, потребляемая нагрузкой с сопротивлением , измеряется косвенным методом и вычисляется в соответствии с формулой

.

Оценки значения тока и величины сопротивления нагрузки и по условиям эксперимента могут быть получены путем прямых однократных измерений с относительными погрешностями, пределы которых оцениваются величинами: % и % соответственно. Определить пределы относительной погрешности, с которой в этих условиях будет измерена мощность потребляемая нагрузкой.

Решение:

В соответствии с изложенным выше, измерение мощности представляет собой обыкновенное нелинейное косвенное измерение. Оценку результата измерения в соответствии с (3.11 [4]) можем записать:

,

где 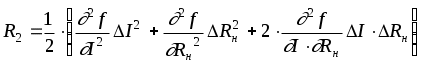 остаточный член разложения исходной функции в ряд Тейлора;

; ; ; ; .

Убедимся в возможности линеаризации исходного уравнения, для чего оценим величину остаточного члена 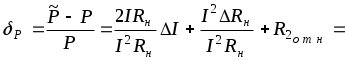. Так как по условию задачи сами оценки значения аргументов и остаются неизвестными, перейдем к относительной форме выражения погрешностей.



,

где :

.

Оценим величину остаточного члена по сравнению с другими погрешностями. Очевидно, что



.

Следовательно, линеаризация исходного уравнения правомерна и остаточным членом разложения можно пренебречь, при этом получаем

.

Принимая во внимание тот факт, что значения аргументов по условию задачи измерялись путем обыкновенных однократных прямых измерений, следует считать, что пределы относительных погрешностей аргументов и определены с использованием информации о классе точности используемых приборов.

Следовательно, для определения пределов относительной погрешности измерения мощности следует воспользоваться формулой (2.35 [4] ), записав ее для относительных погрешностей:

.

Приняв доверительную вероятность , получаем

%.

Учитывая, что суммируются всего две составляющие погрешности, оценим их арифметическую сумму

%.

Так как  , то в качестве границ погрешности результата измерения мощности принимаем доверительные границы при .

Ответ: %, .