лое. Лое. Методические указания по проведению практических занятий по метрологии и измерительной технике для студентов всех специальностей очной формы обучения
 Скачать 1.9 Mb.
|
|
Задача № 2.17 Оценить границы неисключенного остатка методической погрешности измерения напряжения по условиям задачи № 2.15. Решение: Абсолютное значение методической погрешности определяется формулой (см. задачу № 2.15)  .Вычислить точное значение поправки  невозможно, поскольку значения резисторов  и  известны с погрешностями (показания вольтметра  , для которого определяется поправка, считаются const). Оценка абсолютного значения поправки дана в задаче № 2.15 .Учитывая, что функция 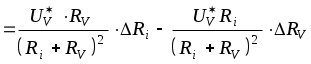 достаточно проста, а погрешности аргументов малы  считаем, что линеаризация исходной функции правомерна. Границы абсолютной погрешности определения величины поправки найдем, воспользовавшись формулой (3.14 [4] ).  .Погрешности аргументов известны в виде границ, т. к. о законе распределения ничего не известно, определяем границы погрешности результата по формуле (2.35) с учетом (3.14). Принимая во внимание тот факт, что приходится суммировать всего две составляющих, оценим максимально возможные границы погрешности определения поправки   (В).Таким образом, границы неисключенного остатка методической погрешности в абсолютной форме  В.Границы неисключенного остатка методической погрешности в относительной форме  %.Ответ:  В;  %.Задача № 2.18 Обработать результаты многократных прямых измерений тока, проведенных одним и тем же прибором за достаточно малый промежуток времени. При измерении получены следующие результаты (в мА): 10,07; 10,10; 10,15; 10,16; 10,17; 10,20; 10,40; 10,13; 10,12; 10,08. Считать, что полученная совокупность результатов свободна от систематических погрешностей и подчиняется нормальному закону распределения. Решение: Из условия задачи следует, что полученная совокупность результатов представляет собой выборку равноточных нормально распределенных данных. Используя формулы раздела 2.3 [4], получаем: 1) Наиболее вероятное значение измеренной величины (оценка действительного значения тока)  (мА);2) Оценка средней квадратичной погрешности (СКП) экспериментальных данных  (мА);3) В полученной совокупности экспериментальных данных седьмой результат  мА существенно отличается от остальных. Проверим, не содержит ли он грубую погрешность?Определим  .Зададим доверительную вероятность  и по таблице №3 Приложения находим допускаемую величину  для выборки из 10 результатов при . ,следовательно, результат мА содержит грубую погрешность и должен быть отброшен. Количество результатов в выборке уменьшается до  .4) Уточняем значения 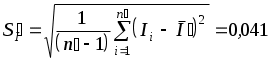 и   (мА) (мА).В оставшейся совокупности результатов следует проверить еще результат  мА. При той же доверительной вероятности для выборки из 9 результатов находим табличное значение  . Определяем  .Так как   , результат измерения мА должен быть оставлен.5) Определим СКП результата измерения (за результат измерения принимается уточненное значение  ) (мА).6) Определим границы доверительного интервала для результата измерений. Так как число обрабатываемых результатов 20, то при определении коэффициента  пользуемся табличными значениями распределения Стьюдента (см. Приложение). Задаем доверительную вероятность и для выборки из 9 наблюдений находим = 2,31.Границы доверительного интервала для результата измерения  (мА).7) Запишем результат измерения с указанием доверительной погрешности (соблюдая все правила метрологии при округлении значения погрешности и значения результата при окончательной записи результата измерений).  мА; ;  ,или 10,099 мА  10,163 мА; ; .Ответ:  мА; ; ,или 10,099 мА 10,163 мА; ; .Примечание: обе записи результата соответствуют требованиям стандарта и являются равнозначными. Задача № 2.19 Для выяснения закона распределения случайных отклонений изготовленных резисторов от номинала было проведено измерение точного значения 200 резисторов из одной партии. Номинальное значение резисторов 300 Ом. В результате предварительной обработки результатов измерений получены следующие данные: Максимальное значение резистора в выборке -  Ом;Минимальное значение резистора в выборке -  Ом;Среднее квадратическое значение отклонений резисторов от номинального значения -  Ом.Примечание: для экономии места вся совокупность полученных результатов измерений резисторов здесь не приводится.В таблице 1 приведены сгруппированные по интервалам данные предварительной обработки отклонений резисторов от номинала. Решение: Для обоснованной формулировки гипотезы о виде закона распределения отклонений резисторов от номинала построим гистограмму опытного распределения, соблюдая все рекомендации, приведенные в 4-6, для чего: 1) Группируем полученные отклонения по интервалам, число которых выбираем –r=11; 2) Определяем ширину интервала, используя (3.6 [4] ),  (Ом),или используя максимальные отклонения резисторов от номинала  (Ом).Округляя расчетное значение h, принимаем ширину интервала равной -  Ома;3) В качестве нижней границы первого интервала для удобства построения гистограммы выбираем не само значение полученного экспериментально отклонения  (Ом),а несколько меньшее число -  (Ом);4) Определив нижнюю границу первого интервала - Ом, определяем границы всех остальных интервалов (например,  и т.д.).5) Подсчитываем число отклонений, попавших в каждый интервал -  (частоты) и определяем значение экспериментальной вероятности попадания отклонений в соответствующий интервал (частости) Все полученные данные и результаты дальнейших промежуточных расчетов заносим (для удобства представления результатов) в таблицу 1. 6) Выбрав (в соответствии с рекомендациями) масштаб по осям, строим гистограмму опытного распределения рисунок . Вид этой гистограммы (сплошные линии на рисунке) позволяет с большой уверенностью предположить, что закон распределения отклонений резисторов от номинала является нормальным. Для окончательного принятия решения о виде закона распределения воспользуемся критерием согласия  (или критерием Пирсона).Для того чтобы использовать критерий согласия , проделаем некоторые промежуточные расчеты, результаты которых также заносим в таблицу 1.7) Определяем нормированную нижнюю границу первого интервала и нормированные верхние границы всех интервала по формуле  ;8) Воспользовавшись таблицей 2 Приложения, находим значение нормированной интегральной функции нормального распределения -  для нижней границы первого интервала и верхних границ каждого интервала;9) Используя формулу (2.28 [4]) находим теоретическое значение вероятности попадания результатов в соответствующий интервал  10) Находим ту часть общего числа имеющихся результатов измерений, которая теоретически должна быть в каждом из интервалов  ,если в какой либо интервал теоретически попадает меньше 5 результатов, то его в обеих гистограммах объединяют с соседним, таеим образом, чтобы в объединенных интервалах оказалось более 5 результатов. Число интервалов - r, определенное в п.1, соответствующим образом изменяется (объединение интервалов при  делается по той причине, что табличные значения -распределения, которыми предстоит пользоваться, рассчитаны для разных степеней свободы k при условии, что все  ).Для рассматриваемой задачи следует объединить 11 интервал с 10 интервалом, что и отражено в таблице. Следует обратить внимание на то, что решение об объединении интервалов можно принимать только после того, как для всех интервалов рассчитано число результатов, которые теоретически должны попадать в каждый из интервалов, и если для каких то интервалов это число оказывается меньше 5 (округлять расчетное число результатов до целого значения не следует). Для иллюстрации степени различия гистограммы опытного распределения и теоретического нормального распределения с тем же числом интервалов изображены на рис. (гистограмма теоретического распределения изображена на рисунке пунктирными линиями, данные взяты из табл. 1); 11) Для каждого интервала вычисляем меру расхождения опытной и теоретической кривой распределения -   и вычисляем величину критерия согласия -  ,где  - число интервалов группирования данных после объединения, если таковое происходило;12) Определяем число степеней свободы для - распределения (или распределения Пирсона), которое определяется соотношением  где s - число независимых связей, наложенных на частости  . Числовое значение параметра s определяется видом теоретического закона распределения, на соответствии которому проверяется опытное распределение. Для нормального закона - s=3 и эти связи следующие, для нормального закона распределения принимаются условия:  (условие нормировки).Таким образом, для рассматриваемой задачи,  ;13) Выбираем доверительную вероятность -  . с которой будем проверять согласие опытного распределения с теоретическим или выбираем уровень значимости критерия - g (. ).Уровень значимости - g должен быть достаточно малым, чтобы была мала вероятность отклонить правильную гипотезу (ошибка первого рода), но не слишком малым, чтобы не увеличивать вероятность принятия ложной гипотезы (не совершить ошибку второго рода). Для практического решения задачи определения согласия опытного распределения с выбранным теоретическим законом рекомендуется выбирать уровень значимости в интервале значений  [6].Для рассматриваемой задачи выбираем  (т.е.  );14) По таблицам - распределения (таблица 5 Приложения) при уровне значимости  и числе степеней свободы к=7 находим граничные значения функции ,  ;15) Принимая во внимание, что  можем сделать вывод, что распределение опытных данных не противоречит нормальному закону, т.е. гипотеза о нормальности закона распределения отклонений резистора от номинального значения может быть принята. Ответ: Закон распределения отклонений резистора от номинального значения  Ом можно с вероятностью считать нормальным со средним квадратическим отклонением   Ом. Рассмотренная в решении примера последовательность действий по применению критерия для проверки согласия опытного распределения с теоретическим входит как составная часть в общий алгоритм обработки результатов многократных прямых измерений при неизвестном заранее законе распределения. |