лое. Лое. Методические указания по проведению практических занятий по метрологии и измерительной технике для студентов всех специальностей очной формы обучения
 Скачать 1.9 Mb.
|
|
2.4. Случайные погрешности 2.4.1. Вопросы для самоконтроля 1) В каком виде может быть представлен закон распределения случайной погрешности? Какие виды законов распределения вам известны? 2) Что понимается под термином “числовые характеристики случайной погрешности”? Назовите известные вам числовые характеристики? Какие из них наиболее часто используются в практике измерений? 3) Что такое нормированный нормальный закон распределения? Для чего нормируют закон распределения? Что понимается под термином “нормированная величина случайной погрешности”? 4) Что понимается под предельной случайной погрешностью при нормальном распределении и при других законах распределения? Какова связь между предельной случайной погрешностью и СКП? 5) Что обозначают символы  ,  и  ? Существует ли связь между ними?6) Дайте определение понятиям “доверительный интервал” и “доверительная вероятность”. Какая величина доверительной вероятности соответствует интервалу предельной случайной погрешности при нормальном распределении? 7) Можно ли определить доверительный интервал для случайной погрешности при неизвестном законе распределения, если оценка СКП известна?8) Доверительный интервал нормально распределенной случайной погрешности результата вычисляется по одной из следующих формул:  или  .О чем говорит первая и вторая форма записи? Одинаковый ли этот интервал в первом и во втором случаях, если доверительная вероятность  в обоих случаях одинакова?9) Что означают термины “теоретически допускаемое максимальное по модулю нормированное отклонение” и “максимальное по модулю нормированное отклонение”? Как определяются и для чего используются эти величины? 10) Какая форма представления результата (с использованием точечных или интервальных оценок случайной погрешности) предпочтительна и почему? 2.4.2. Примеры решения задач Задача № 2.8 Погрешность измерения некоторой ФВ распределена по нормальному закону. Определить вероятность того, что случайная погрешность отдельного результата не превысит более чем в 1,5 раза значение среднеквадратической погрешности (СКП). Решение: По условию задачи  . Пользуясь формулой (2.12 [4] ), определяем нормированные границы интервала (при M[ΔXсл]=0). .Так как интервал симметричный, то по таблице №1 Приложения находим значение интеграла вероятности, соответствующее  ; .Ответ:  .Задача № 2.9 Случайная погрешность измерения напряжения распределена по нормальному закону. При обработке результатов измерений получены следующие оценки погрешностей: систематическая погрешность  мВ; оценка СКП  мВ. Определить вероятность того, что результат измерения отличается от истинного значения не более чем на  мВ.Решение: 1. Определим вероятность события при условии, что поправка на систематическую погрешность не вводится. Наличие систематической погрешности делает интервал несимметричным относительно нуля. В этом случае доверительная вероятность определяется следующим образом:  ,где:  нижняя граница доверительного интервала; верхняя граница доверительного интервала.Определим нормированные границы доверительного интервала:  ; .Для определения доверительной вероятности в случае несимметричного интервала воспользуемся формулой (2.28 [4] ). Значение нормированной интегральной функции нормального распределения определяем по таблице №2 Приложения.  .Ответ:  , при  мВ.2. Определим вероятность события при условии, что на систематическую погрешность вводится поправка, т. е. результаты измерений исправляются прежде, чем проводится статобработка. В этом случае доверительный интервал будет симметричным мВ и дальнейшее решение не отличается от решения задачи № 2.8.Нормированные границы доверительного интервала  . .Ответ:  ,при  . Задача № 2.10 Случайная погрешность измерения сопротивления распределена по нормальному закону. Оценка СКП  Ом. Определить границы симметричного доверительного интервала, за которые с вероятностью  не выйдет случайная погрешность отдельного результата измерений.Решение: Границы симметричного доверительного интервала определяется формулой (2.22 [4] ).  (Ом).По таблице №1 Приложения для  находим значение безразмерного коэффициента  .Следовательно,  (Ом).Ответ: с доверительной вероятностью погрешность отдельного результата измерения не выйдет за границы  Ом. Задача № 2.11 При измерении емкости конденсатора были получены следующие результаты (в пФ):
Анализ результатов показывает, что 11 результат существенно отличается от остальных в совокупности полученных результатов. Требуется проверить, не содержит ли этот результат грубую погрешность. Закон распределения погрешности считать нормальным. Решение: 1. Определим параметры распределения с учетом всех результатов по формулам (2.16 и 2.17 [4] ). 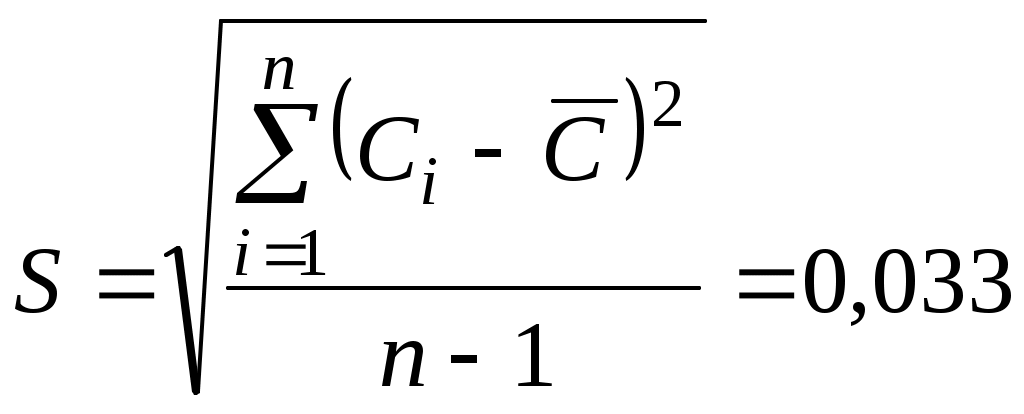 пФ; пФ.2. Для сомнительного результата (в соответствии с 2.33 [4] ) определяем величину нормированного отклонения  .3. Зададим уровень доверительной вероятности  и по таблице №3 Приложения для числа наблюдений п = 15 найдем табличное значение βГ =2,997 (допускаемая граница нормированного отклонения для выборки из 15 наблюдений при доверительной вероятности 0,95).Так как β*11 = 3,15  = 2,997, то 11 результат содержит грубую погрешность и должен быть отброшен.Ответ: с доверительной вероятностью  11-й результат содержит грубую погрешность.5. Определим, насколько точнее будут определены параметры распределения без 11-го результата. Воспользовавшись формулами (2.16) и (2.17) для выборки из 14-ти результатов, получаем уточненные значения:  пФ;  пФ.Таким образом, без влияния результата, содержащего грубую погрешность, доверительные границы результата измерения будут определены в два раза точнее, т. к.  .2.4.3. Задачи для самостоятельного решения 1. Как отразится на результате измерения следование русской поговорке: “Семь раз отмерь один отрежь”? Во сколько раз точнее будет получен результат, если каждое измерение осуществляется с погрешностью  %?2. Каков должен быть объем выборки п, чтобы с вероятностью 0,99 точность оценки математического ожидания результата измерений  была, ±0,2, если  ?3. При изготовлении деталей допускаемое случайное отклонение параметров от номинального значения чаще всего выбирают равным  , что соответствует доверительной вероятности  (закон распределения погрешностей нормальный). На сколько изготовленных деталей будет приходиться в среднем одна забракованная? Как изменится эта ситуация, если повысить требования к точности (т. е. сузить границы доверительного интервала до  )? Что произойдет, если расширить границы до  ?4. С помощью вольтметра, имеющего СКП  =  В, по результатам 10 измерений получена оценка напряжения с границами доверительного интервала ΔŪРдов=±0,01В. Сколько потребуется измерений, чтобы такая же точность с той же доверительной вероятностью была получена другим вольтметром со СКП =  В?5. В результате большого числа измерений был определен доверительный интервал для ЭДС термопары. С доверительной вероятностью 0, 997 этот интервал оказался следующим - 17,73 мВ Е 17,27 мВ. Определить СКП измерения ЭДС в предположении нормального закона распределения. 2.5. Математическая обработка результатов измерений 2.5.1. Вопросы для самоконтроля Правила суммирования составляющих погрешностей. Правила округления значений погрешности и результата при окончательной записи. 1) Сформулируйте правила суммирования составляющих систематической и составляющих случайной погрешностей. 2) Что понимается под термином “общая погрешность результата измерений”? Как она определяется? 3) Сформулируйте основные правила округления значения погрешности и значения результата измерения при окончательной записи. 4) Сформулируйте основные правила записи результата, когда систематическая и случайная погрешности указываются раздельно. Когда используется такая запись? 5) Сформулируйте основные правила записи результата, когда границы погрешностей результата несимметричны. 6) Сформулируйте основные правила записи результата с указанием общей погрешности. Когда используется такая форма записи? Погрешности средств измерений. Обработка результатов прямых однократных измерений. 1) По каким признакам группируются СИ при выборе способа нормирования предела допускаемой основной погрешности? 2) Дайте определение понятиям “предел допускаемой основной погрешности” и “класс точности” средства измерений. Что определяют эти понятия? 3) Как нормируется предел допускаемой основной погрешности и как эта величина обозначается на шкале или корпусе прибора, если у СИ преобладает: а) аддитивная погрешность; б) мультипликативная погрешность; в) учитываются обе составляющие погрешности. 4) Как выбирается нормирующая величина N при определении приведенной погрешности для присвоения СИ класса точности. 5) Какую погрешность СИ (систематическую, случайную или общую) определяет класс точности? 6) Дайте определение понятию “дополнительные погрешности СИ”. Какие они бывают? Когда и почему возникают? Какие способы нормирования их вам известны?   7) Расшифруйте условные обозначения классов точности: 1,5; 1,5 ; 1,5 ;  .8) Объясните, как, используя информацию о классе точности в виде условного обозначения на шкале или корпусе прибора, определить абсолютную и относительную погрешности результата измерения, если условное обозначение имеет вид: а   ) 1,5; б) 1,5 ; в) 1,5 ; г) .9) Сформулируйте правила, по которым определяется погрешность результата измерения для случая использования СИ в реальных условиях эксплуатации. 10) Опишите общий порядок действий (алгоритм обработки) при определении погрешности результата однократных технических измерений. Обработка результатов прямых многократных (статистических) измерений. 1) Сформулируйте полный алгоритм обработки нормально распределенных данных. 2) Сформулируйте полный алгоритм обработки опытных данных, распределение которых заранее неизвестно. 3.)Что такое “гистограмма опытного распределения”? Для чего она строится? 4) Что означают термины “упорядоченные опытные данные” и “сгруппированные опытные данные”? Для чего проводятся эти действия над опытными данными? 5) Какие условия необходимо соблюдать, выбирая число интервалов при группировании данных? 6) Какие правила необходимо соблюдать при построении гистограммы опытного распределения? 7) Почему число результатов сгруппированных данных, попадающих в каждый интервал, должно удовлетворять условию  ?8) Что означает термин “проверка согласия опытного распределения с теоретическим”. По каким критериям это согласие проверяется? При каких условиях эта проверка может осуществляться? 9) Что является мерой расхождения опытной и теоретической кривой распределения в критерии согласия Пирсона (критерии  )?10) Что такое уровень значимости критерия согласия и как он выбирается? |