Электротехника. Методические указания предназначены для студентов закончивших неэлектрических специальностей при изучении электротехники по курсу "эоэ и мпт", 1
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
|
Таблица 2 (продолжение)
б) форма записи комплексных чисел показательная и алгебраическая Рассмотрим несколько примеров перевода комплексных чисел из алгебраической формы в показательную: где а и b- проекции на ось действительных и мнимых чисел соответственно. Резонанс напряжений Резонанс напряжений возможен лишь в электрической цепи, содержащий последовательно включённые реактивные сопротивления XL и XC. Условием возникновения резонанса напряжений является равенство XL =XC или ωL=1/(ωc). Резонанс токов. Резонанс токов возможен в электрической цепи при параллельном включении реактивных сопротивлений XL и XC. Условием появления резонанса тока является равенство реактивных проводимостей соответствующих ветвей: b  L= bС ; L= bС ; где bL = Электрическая схема с параллельным включением реактивных сопротивлений XL и XC изображена на рис. 4. 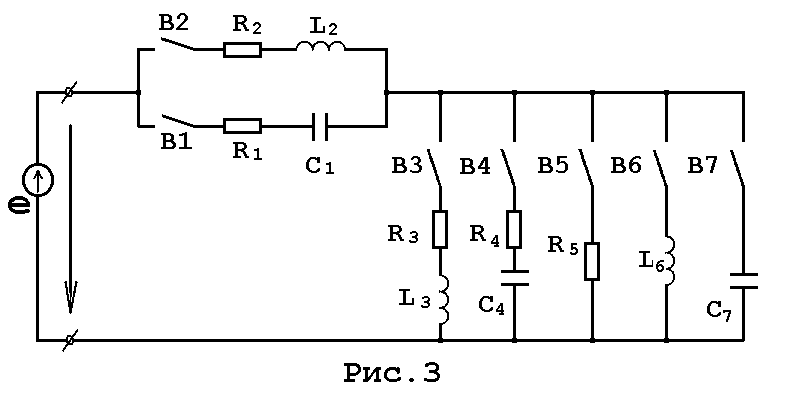  Задача3. Анализ трёхфазной электрической цепи при схеме соединения приёмников “ звездой”. В трёхфазную сеть с симметричной системой линейных напряжений UЛ включён трёхфазный потребитель электроэнергии, фазы которого имеют комплексные сопротивления Za, Zb, Zc и соединены “звездой”. Определить: линейные и фазные ток; активную Р, реактивную Q и полную S мощности потребителя; показания приборов: амперметра и ваттметра; построить векторную диаграмму токов и напряжений; Краткие теоретические положения. Трёхфазная система питания потребителей электроэнергии. Трёхфазная система питания электрических цепей представляет собой совокупность трёх синусоидальных ЭДС или напряжений, одинаковых по частоте и амплитудному значению, сдвинутых по фазе относительно друг друга на угол 120. еА = Em sin wt; eВ = Em sin (wt-2П/3) eC = Em sin (wt+2П/3). В симметричных источниках питания максимальные значения ЭДС равны, соответственно равны и действующие значения ЭДС EA=EB=EC=Eф. Пренебрегая внутренним сопротивлением источника, можно принять соответствующие ЭДС источника равными напряжениям, действующим на его зажимах: EА=UА, EВ=UВ, EС=UС. Комплексные напряжения симметричного источника питания могут быть представлены системой уравнений:  UА = Uф ej0 = Uф, UВ = Uф e-j120 = Uф(-0,5- j √3/2) , UС = Uф ej120 = Uф(-0,5+ j √3/2) Фазным называется напряжение между началом и концом фазы. Линейным назовём напряжение между двумя линиями или между началами двух фаз. Соотношение между линейным и фазным напряжениями симметричного источника питания: Uл = √3 Uф. Трёхфазные электрические цепи при соединении фаз приёмников “звездой”. При соединении фаз трёхфазного источника питания “звездой” концы фаз источника X,Y,Z объединены в общую нейтральную точку N, а начала фаз А,В,С подключаются к соответствующим линейным проводам Аа, Вв, Сс. Аналогичным образом при соединении трёхфазных потребителей “звездой” объединяются в нейтральную точку n концы его фаз x,y,z, а начала фаз а,в,с подключаются к линейным проводам. Линейные токи Iл в питающих линиях имеют условно-положительное направление от источника энергии к приёмнику. При соединении приёмника энергии по схеме “звезда” линейные токи IА,IВ,IС одновременно являются и фазными токами приёмника Iа,Iв,Iс, т.е. IА= Iа; IВ = Iв ; IС = Iс. Трёхфазные источники питания практически всегда выполняются симметричными. Трёхфазные потребители электроэнергии могут быть симметричными и несимметричными. Для симметричных приёмников электроэнергии справедливы соотношения, полученные для трёхфазных симметричных источников питания. При этом Uа= Ub=Uc=Uф; UАВ = UВС =UСА = UЛ; Za=Zb=Zc=Zф; Cosφа = cosφb = cosφc = Cosφф ; UЛ=√3Uф. Для несимметричных приёмников не все эти соотношения соблюдаются. При анализе трёхфазных электрических цепей широко используется метод комплексных чисел. При несимметричной нагрузке комплексные сопротивления фаз приёмника не одинаковы (Za≠Zb≠Zc), при этом комплексное напряжение UnN, действующее между нейтральными точками N и n системы, определяют по методу двух узлов ַU  nN= nN= |
